{
"cells": [
{
"cell_type": "markdown",
"id": "578f9d15-3df9-461f-befc-ab77c381a96d",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"(Intro_PyTensor)=\n",
"\n",
"# What is PyTensor?\n",
":::{post} August 16, 2025 \n",
":tags: introduction, worked examples, tutorial\n",
":category: beginner, explanation \n",
":author: Jesse Grabowski, Ricardo Vieira\n",
":::\n",
"\n",
"A library to define, manipulate, and compile computational graphs.\n",
"\n",
"\n",
"## Let's break it apart\n",
"A library to (1.) define, (2.) manipulate, and (3.) compile (0.) computational graphs."
]
},
{
"cell_type": "markdown",
"id": "0427f803",
"metadata": {},
"source": [
"## Prepare Notebook"
]
},
{
"cell_type": "code",
"execution_count": 1,
"id": "701a0893",
"metadata": {},
"outputs": [],
"source": [
"import matplotlib.pyplot as plt\n",
"\n",
"\n",
"plt.style.use(\"seaborn-v0_8\")\n",
"\n",
"%config InlineBackend.figure_format = \"retina\""
]
},
{
"cell_type": "markdown",
"id": "bdf5f119-c085-48a1-b6b0-733ed4921303",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## (0.) Computational graph\n",
"\n",
"Any program implies a computational graph. In PyTensor we're mostly focusing on static, array-based (i.e, numpy) programs with some branching and looping primitives. PyTensor is hackable, and can be easily extended to represent arbitrary types and operations. That said, its usefulness quickly vanishes as you venture out of its area of focus.\n",
"\n",
"Everyone here is likely familar with the idea of a computation graph, but let's look at a quick example anyway. Consider a program that computes $z = x + y$. Here we have:\n",
"\n",
"- Two symbolic inputs, $x$ and $y$\n",
"- An operator, $+$, that takes several inputs and maps them to a single output\n",
"- A symbolic output, $z$\n",
"\n",
"Visualized:"
]
},
{
"cell_type": "code",
"execution_count": 2,
"id": "f1890c77",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [],
"source": [
"import graphviz as gr\n",
"\n",
"\n",
"def draw_graph(edge_list, node_props=None, edge_props=None, graph_direction=\"UD\"):\n",
" \"\"\"Utility to draw a causal (directed) graph\"\"\"\n",
" g = gr.Digraph(\n",
" graph_attr={\n",
" \"rankdir\": graph_direction,\n",
" \"ratio\": \"0.3\",\n",
" \"overlap\": \"vpsc\",\n",
" \"splines\": \"true\",\n",
" \"mode\": \"sgd\",\n",
" \"lheight\": \"4\",\n",
" },\n",
" engine=\"dot\",\n",
" )\n",
"\n",
" edge_props = {} if edge_props is None else edge_props\n",
" for e in edge_list:\n",
" props = edge_props[e] if e in edge_props else {}\n",
" g.edge(e[0], e[1], **props)\n",
"\n",
" if node_props is not None:\n",
" for name, props in node_props.items():\n",
" g.node(name=name, **props)\n",
" return g\n"
]
},
{
"cell_type": "markdown",
"id": "870d7457",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"While this DAG is boring and obvious, it highlights that there are two types of nodes:\n",
"\n",
"- Variables\n",
"- Operations\n",
"\n",
"We can also distinguish between \"root variables\", like $x$ and $y$, intermediate variables (we don't have any here :( ) and output variables ($z$). These differences will return in a few slides!"
]
},
{
"cell_type": "code",
"execution_count": 3,
"id": "e0396698",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"data": {
"image/svg+xml": [
"\n",
"\n",
"\n",
"\n",
"\n"
],
"text/plain": [
""
]
},
"execution_count": 3,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"draw_graph([(\"x\", \"+\"), (\"y\", \"+\"), (\"+\", \"z\")])"
]
},
{
"cell_type": "markdown",
"id": "97944cd3",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## (1.) Definition \n",
"In PyTensor, you define a computational graph explicitly, starting with _placeholder_ input variables. From these inputs you build more intermediate variables by applying operators (like $+$), which can then be treated either as outputs, or as intermediate variables for further computation.\n",
"\n",
"To reduce the learning barrier, Pytensor was designed to look like numpy code. But be aware that it's not! Let' look at some differences."
]
},
{
"cell_type": "code",
"execution_count": 4,
"id": "ed6d4a86d7398eca",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"text/plain": [
"array([0. , 0.69314718, 1.31326169])"
]
},
"execution_count": 4,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"import numpy as np\n",
"\n",
"\n",
"# Numpy\n",
"x = np.array([0, 1, np.e]) # Actual numbers\n",
"y = np.log(1 + x) # Actual computation\n",
"y # Actual result"
]
},
{
"cell_type": "markdown",
"id": "559a56aa",
"metadata": {},
"source": [
"Now, let's see how we can use PyTensor to define a computational graph for the same operation."
]
},
{
"cell_type": "code",
"execution_count": 5,
"id": "f10206d3",
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(Log.0, pytensor.tensor.variable.TensorVariable)"
]
},
"execution_count": 5,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"import pytensor\n",
"import pytensor.tensor as pt\n",
"\n",
"\n",
"# Pytensor\n",
"x = pt.tensor(shape=(3,), dtype=\"float64\") # Symbolic vector\n",
"y = pt.log(1 + x) # Symbolic computation\n",
"y, type(y)"
]
},
{
"cell_type": "markdown",
"id": "cd6ebfa4",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"The most important thing to grok here is that `y` is not a number! It's a symbol. Specifically, it's the output of a `Log` operation, so we see the name `Log.0`. The type is a `TensorVariable`, which is a basic unit of symbolic computation.\n",
"\n",
"Notice how Pytensor is straddling a line between a computer algebra system like sympy or maple, and a tensor library like numpy."
]
},
{
"cell_type": "markdown",
"id": "904410ca",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"A key tool when working with Pytensor is {func}`~pytensor.dprint`. It's short for \"debug print\", and it shows you a text representation of a graph. It's always a good idea to look at the graph pytensor is generating for your graph, because it shows you exactly what is going on. Admittedly, they take a bit of getting used to reading."
]
},
{
"cell_type": "code",
"execution_count": 6,
"id": "f6f5731649ea29c7",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Log [id A]\n",
" └─ Add [id B]\n",
" ├─ ExpandDims{axis=0} [id C]\n",
" │ └─ 1 [id D]\n",
" └─ [id E]\n"
]
},
{
"data": {
"text/plain": [
""
]
},
"execution_count": 6,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"y.dprint()"
]
},
{
"cell_type": "markdown",
"id": "e913e973",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"PyTensor can also generate visual representations of your graph. You will be forgiven if you think this is a much better way to view a graph. It's great, but doesn't scale well at all. For large graphs, the output is completely unreadable. If anyone is interested in developing tensorboard-like tools that will allow for interactive investigation of a graph, PRs are accepted!\n",
"\n",
"That said, here's the visual representation of our graph. It's very similar to our $z = x + y$ graph, with a some extra computational accoutrement. "
]
},
{
"cell_type": "code",
"execution_count": 7,
"id": "25e22315",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"image/svg+xml": [
""
],
"text/plain": [
""
]
},
"execution_count": 7,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"from IPython.display import SVG\n",
"\n",
"from pytensor.printing import pydotprint\n",
"\n",
"\n",
"SVG(pydotprint(y, return_image=True, format=\"svg\"))"
]
},
{
"cell_type": "markdown",
"id": "8bf95ff2-1c44-4c98-9dbc-de76b94c57d2",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"For those curious: This kind of graph is a bi-partite, directed, acyclic graph composed of interconnected Variable -> Apply -> Variable nodes.\n",
"\n",
"Apply nodes connect input variables to output variables, via a specific operator. Variables have a type and can have an owner (the Apply node that creates them) or not (if they are root placeholder variables).\n",
"\n",
"Here is a schematic of the $z = x + y$ graph again, but this time with annotations that show how it is represented in Pytensor. I always felt it was upside-down; perhaps that feeling will help you to understand what you're looking at. Read it from top-to-bottom, but with the flow of computation running against the arrows:\n",
"\n",
"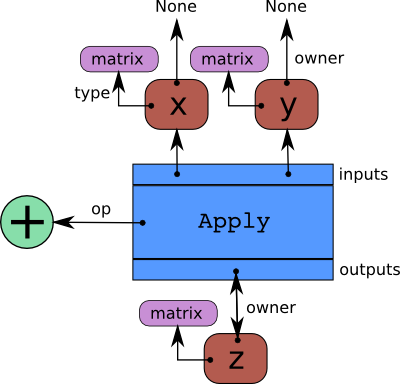"
]
},
{
"cell_type": "markdown",
"id": "6ec992ea",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"We can see these definitions in action by looking at properties of `y`. We've already seen that `type(y)` is a `TensorVariable`. With the exception of root variables, all `TensorVariables` have an `owner`, which is the `Apply` node that created it. \n",
"\n",
"In this case, the owner of `y` is `Log(Add.0)`. `Add.0` is the name of the output of an `Add` `Op`, so `y` is the result of a `Log` applied to an `Add`."
]
},
{
"cell_type": "code",
"execution_count": 8,
"id": "2c0a5be5591f936",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"data": {
"text/plain": [
"(Log(Add.0), pytensor.graph.basic.Apply)"
]
},
"execution_count": 8,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"y.owner, type(y.owner)"
]
},
{
"cell_type": "markdown",
"id": "3ef053ec",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"Looking at the schematic again, note that there is a conceptual difference between `Apply` (which is a big box that handles a bunch of stuff) and an `Op`, which is the actual type of computation being done. \n",
"\n",
"In this case, the specific Op is an `Elemwise`, which is a meta-Op that broadcasts a scalar computation (in this case `scalar_op = log`) across a tensor input. It makes it an elementwise operation... hence \"Elemwise Op\"."
]
},
{
"cell_type": "code",
"execution_count": 9,
"id": "bc75e500fb9ece2f",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"data": {
"text/plain": [
"(Elemwise(scalar_op=log,inplace_pattern=),\n",
" pytensor.tensor.elemwise.Elemwise)"
]
},
"execution_count": 9,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"y.owner.op, type(y.owner.op)"
]
},
{
"cell_type": "markdown",
"id": "5e2e3fac",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"We can also check the outputs of the `Apply`. This is, of course, `y` itself!"
]
},
{
"cell_type": "code",
"execution_count": 10,
"id": "f1bb3439391f2509",
"metadata": {
"scrolled": true,
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"data": {
"text/plain": [
"([Log.0], True)"
]
},
"execution_count": 10,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"y.owner.outputs, y.owner.outputs == [y]"
]
},
{
"cell_type": "markdown",
"id": "75685087",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"Finally, there's the inputs. This is `Add.0`, which represents `1 + x`"
]
},
{
"cell_type": "code",
"execution_count": 11,
"id": "c6f97556431c818f",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"data": {
"text/plain": [
"[Add.0]"
]
},
"execution_count": 11,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"y.owner.inputs"
]
},
{
"cell_type": "markdown",
"id": "b57e98dc",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"From here, the story begin again, and we can keep climbing up the graph until the root variable, `x`. I'll spare you, though"
]
},
{
"cell_type": "code",
"execution_count": 12,
"id": "316c181a13627039",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Add [id A]\n",
" ├─ ExpandDims{axis=0} [id B]\n",
" │ └─ 1 [id C]\n",
" └─ [id D]\n"
]
},
{
"data": {
"text/plain": [
""
]
},
"execution_count": 12,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"y.owner.inputs[0].dprint() # And the story begins again"
]
},
{
"cell_type": "markdown",
"id": "3a916500-4dfe-4ef0-90ac-84f5de9f7ce2",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## (2) Manipulation\n",
"\n",
"So far, nothing we've seen is special. Maybe it's a nice API for writing functions, but it's not at all clear why the program `y = pt.log(1 + x)` is better than the following Python program:\n",
"\n",
"```py\n",
"def log1p(x):\n",
" return np.log(1 + x)\n",
" \n",
"y = log1p(x)\n",
"```\n",
"\n",
"Actually, this is the exact API that JAX offers! Setting aside JAX, we might even take this function and decorate it with `@numba.njit`, potentially getting big speedups. What does pytensor offer us?\n",
"\n",
"The answer is that PyTensor is able to **manipulate** the computation graph. Furthermore, these manipulations are done within Python. JAX, for example, is able to trace the above function to construct a computational graph. But the graph representation is not front-and-center, and it's no obvious how to use it. In PyTensor, you are meant to be working direcly on graphs!\n",
"\n",
"There are three important graph operations to consider:\n",
"\n",
"1. Replacement\n",
"2. Rewriting\n",
"3. Transformation\n",
"\n",
"We will look at each of these in turn."
]
},
{
"cell_type": "markdown",
"id": "6ec7dfd0",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"### Graph Replacement\n",
"\n",
"The simplest graph operation is a **replace**. We simply take one operation and swap it out for another. Consider the following graph:"
]
},
{
"cell_type": "code",
"execution_count": 13,
"id": "70351014",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Add [id A]\n",
" ├─ ExpandDims{axis=0} [id B]\n",
" │ └─ 1 [id C]\n",
" └─ Sin [id D]\n",
" └─ Mul [id E]\n",
" ├─ ExpandDims{axis=0} [id F]\n",
" │ └─ 6.283185307179586 [id G]\n",
" └─ b [id H]\n"
]
},
{
"data": {
"text/plain": [
""
]
},
"execution_count": 13,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"a = pt.tensor(\"b\", shape=(None,))\n",
"b = 2 * pt.pi * a\n",
"c = pt.sin(b)\n",
"d = 1 + c\n",
"d.dprint()"
]
},
{
"cell_type": "markdown",
"id": "87f8371c",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"If, for some reason, we wanted to do replace `pt.sin(b)` with `pt.cos(b)`, we could do so with the `graph_replace` function. The subgraph we want to target is `c`, and the top-level output is `d`, so we do it as follows:"
]
},
{
"cell_type": "code",
"execution_count": 14,
"id": "a20df8d6",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Add [id A]\n",
" ├─ ExpandDims{axis=0} [id B]\n",
" │ └─ 1 [id C]\n",
" └─ Cos [id D]\n",
" └─ Mul [id E]\n",
" ├─ ExpandDims{axis=0} [id F]\n",
" │ └─ 6.283185307179586 [id G]\n",
" └─ b [id H]\n"
]
},
{
"data": {
"text/plain": [
""
]
},
"execution_count": 14,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"from pytensor.graph.replace import graph_replace\n",
"\n",
"\n",
"z2 = graph_replace(d, {c: pt.cos(b)})\n",
"z2.dprint()"
]
},
{
"cell_type": "markdown",
"id": "7ceffb26",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"This might seem like a silly example, but one-to-one transformations are quite common! For example, suppose we had a graph with a random variable, and we wanted to replace the random variable with a root variable, transforming it into a function. We can do that with graph replace too:"
]
},
{
"cell_type": "code",
"execution_count": 15,
"id": "5856f780",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Exp [id A]\n",
" └─ normal_rv{\"(),()->()\"}.1 [id B]\n",
" ├─ RNG() [id C]\n",
" ├─ [10] [id D]\n",
" ├─ ExpandDims{axis=0} [id E]\n",
" │ └─ 0 [id F]\n",
" └─ ExpandDims{axis=0} [id G]\n",
" └─ 1 [id H]\n"
]
},
{
"data": {
"text/plain": [
""
]
},
"execution_count": 15,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"x = pt.random.normal(loc=0, scale=1, size=(10,))\n",
"y = pt.exp(x)\n",
"y.dprint()"
]
},
{
"cell_type": "code",
"execution_count": 16,
"id": "0271d4bd",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Exp [id A]\n",
" └─ x_input [id B]\n"
]
},
{
"data": {
"text/plain": [
""
]
},
"execution_count": 16,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"x_input = pt.tensor(\"x_input\", shape=(10,))\n",
"y2 = graph_replace(y, {x: x_input})\n",
"y2.dprint()"
]
},
{
"cell_type": "markdown",
"id": "08ccb932",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"#### Vectorization\n",
"\n",
"A less trivial type of graph replacement is *vectorization*. This is also a one-to-one replacement, but this time things are somewhat more complicated, because it changes the meaning of the graph. Pytensor will automatically reason about the broadcasting operations that need to happen to accomplish the replacement.\n",
"\n",
"This time, I make a graph where all the inputs are specifically declared to be scalars. Notice how this information flows down the graph: since `x` is scalar, and the `Op`s `log` and `add` are elemwise, the output `y` is also a scalar."
]
},
{
"cell_type": "code",
"execution_count": 17,
"id": "05efd44a",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Log [id A] \n",
" └─ Add [id B] \n",
" ├─ 1 [id C] \n",
" └─ x [id D] \n"
]
},
{
"data": {
"text/plain": [
""
]
},
"execution_count": 17,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"x = pt.dscalar(\"x\")\n",
"y = pt.log(1 + x)\n",
"y.dprint(print_type=True)"
]
},
{
"cell_type": "markdown",
"id": "bd514d05",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"Suppose that instead of a scalar `x`, we want to use this function for a vector input. If we naively try to `graph_replace` here, we will get a shape error"
]
},
{
"cell_type": "code",
"execution_count": 18,
"id": "2af1c20e",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Cannot convert Type Vector(float64, shape=(?,)) (of Variable x_vec) into Type Scalar(float64, shape=()). You can try to manually convert x_vec into a Scalar(float64, shape=()).\n"
]
}
],
"source": [
"x_vec = pt.tensor(\"x_vec\", shape=(None,))\n",
"try:\n",
" graph_replace(y, {x: x_vec})\n",
"except Exception as e:\n",
" print(e)"
]
},
{
"cell_type": "markdown",
"id": "1bb040e9",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"Instead, use `vectorize_graph`!"
]
},
{
"cell_type": "code",
"execution_count": 19,
"id": "429d224f",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Log [id A] \n",
" └─ Add [id B] \n",
" ├─ ExpandDims{axis=0} [id C] \n",
" │ └─ 1 [id D] \n",
" └─ x_vec [id E] \n"
]
},
{
"data": {
"text/plain": [
""
]
},
"execution_count": 19,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"from pytensor.graph.replace import vectorize_graph\n",
"\n",
"\n",
"y_vec = vectorize_graph(y, {x: x_vec})\n",
"y_vec.dprint(print_type=True)"
]
},
{
"cell_type": "markdown",
"id": "539a6d85",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"### Rewrites\n",
"\n",
"Rewrites are at the heart of pytensor's usefulness. Pytensor maintains large databases of useful graph transformations. These can be applied to acheive a number of goals."
]
},
{
"cell_type": "markdown",
"id": "ff07ef2c",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"#### Scalarization\n",
"\n",
"We can even undo vectorization -- scalarization?\n",
"\n",
"Here's the original graph:"
]
},
{
"cell_type": "code",
"execution_count": 20,
"id": "82e05376",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Subtensor{i} [id A]\n",
" ├─ Log [id B]\n",
" │ └─ Add [id C]\n",
" │ ├─ ExpandDims{axis=0} [id D]\n",
" │ │ └─ 1 [id E]\n",
" │ └─ x_vec [id F]\n",
" └─ 0 [id G]\n"
]
},
{
"data": {
"text/plain": [
""
]
},
"execution_count": 20,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"y_vec[0].dprint()"
]
},
{
"cell_type": "markdown",
"id": "3a5bab67",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"Notice how the indexing operation has been pushed down to the input!"
]
},
{
"cell_type": "code",
"execution_count": 21,
"id": "e3c49b4c",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Log [id A]\n",
" └─ Add [id B]\n",
" ├─ 1.0 [id C]\n",
" └─ Subtensor{i} [id D]\n",
" ├─ x_vec [id E]\n",
" └─ 0 [id F]\n"
]
},
{
"data": {
"text/plain": [
""
]
},
"execution_count": 21,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"from pytensor.graph import rewrite_graph\n",
"\n",
"\n",
"rewrite_graph(y_vec[0]).dprint()"
]
},
{
"cell_type": "markdown",
"id": "6dce4025",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"#### Stabilization\n",
"\n",
"Calling `rewrite_graph` without any arguments will trigger many rewrites to be applied. If you have a more specific objective, you can ask for specific types of rewrites. For example, the `stabilize` tag includes rewrites that can transform your graph into a form that is more numerically stable"
]
},
{
"cell_type": "code",
"execution_count": 22,
"id": "c1b3d7c7",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Log [id A] \n",
" └─ Add [id B] \n",
" ├─ ExpandDims{axis=0} [id C] \n",
" │ └─ 1 [id D] \n",
" └─ x [id E] \n"
]
},
{
"data": {
"text/plain": [
""
]
},
"execution_count": 22,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"x = pt.tensor(\"x\", shape=(None,))\n",
"y = pt.log(1 + x)\n",
"y.dprint(print_type=True)"
]
},
{
"cell_type": "code",
"execution_count": 23,
"id": "91174dfd",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Log1p [id A]\n",
" └─ x [id B]\n"
]
},
{
"data": {
"text/plain": [
""
]
},
"execution_count": 23,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"stable_y = rewrite_graph(y, include=(\"stabilize\",))\n",
"stable_y.dprint()"
]
},
{
"cell_type": "markdown",
"id": "e65bb491",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"source": [
"There are many more types of rewrites, and we will see them shortly. But first we need to do a Quinten Tarintino and show things somewhat out of order. "
]
},
{
"cell_type": "markdown",
"id": "290f088c",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Graph-to-graph transformations\n",
"\n",
"The most powerful feature of pytensor is to take a graph and return another graph. \n",
"\n",
"We've already seen one example of this in `vectorization`. We included it above because it \"looks like\" `graph_replace`, in the sense that you target a single node for replacement. But as we saw, `vectorize_graph` returns an entirely new graph, with new shapes.\n",
"\n",
"The canonical example of a graph-to-graph transformation is automatic differentiation. If we know the derivative of every `Op` in our graph, we work backwards and follow the chain rule to construct a gradient graph from the graph of a scalar loss function.\n",
"\n",
"The cryptic Op called `Second` means: keep the second input after broadcasting the shape with the first.\n",
"It's the same as `np.broadcast_arrays(x, y)[1]`"
]
},
{
"cell_type": "code",
"execution_count": 24,
"id": "c455a4c9",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"True_div [id A]\n",
" ├─ Second [id B]\n",
" │ ├─ Log1p [id C]\n",
" │ │ └─ x [id D]\n",
" │ └─ ExpandDims{axis=0} [id E]\n",
" │ └─ Second [id F]\n",
" │ ├─ Sum{axes=None} [id G]\n",
" │ │ └─ Log1p [id C]\n",
" │ │ └─ ···\n",
" │ └─ 1.0 [id H]\n",
" └─ Add [id I]\n",
" ├─ ExpandDims{axis=0} [id J]\n",
" │ └─ 1 [id K]\n",
" └─ x [id D]\n"
]
},
{
"data": {
"text/plain": [
""
]
},
"execution_count": 24,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"from pytensor.gradient import grad\n",
"\n",
"\n",
"grad_y = grad(stable_y.sum(), wrt=x)\n",
"grad_y.dprint()"
]
},
{
"cell_type": "markdown",
"id": "5c0484ee",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"#### Quick digression: back to rewrites!\n",
"\n",
"Gradient graphs tend to be complex, so it's nice to simplify them. \n",
"\n",
"One type of simplification is *canonicalization*. It converts a graph into a \"standard\" form. Other rewrites can expect and reason from this form. I think you'll agree this form is much nicer."
]
},
{
"cell_type": "code",
"execution_count": 25,
"id": "1bef9b01",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"True_div [id A]\n",
" ├─ [1.] [id B]\n",
" └─ Add [id C]\n",
" ├─ [1.] [id B]\n",
" └─ x [id D]\n"
]
},
{
"data": {
"text/plain": [
""
]
},
"execution_count": 25,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"rewrite_graph(grad_y, include=(\"canonicalize\",)).dprint()"
]
},
{
"cell_type": "markdown",
"id": "97a7c16b",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"We can also compose rewrites! In this next example, we both canonicalize, then apply specializations to get computational speedups.\n",
"\n",
"This also reveals the \"final form\" of the gradient: $\\log(1 + x) = \\frac{1}{1 + x}$"
]
},
{
"cell_type": "code",
"execution_count": 26,
"id": "0262e4ba",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Reciprocal [id A]\n",
" └─ Add [id B]\n",
" ├─ [1.] [id C]\n",
" └─ x [id D]\n"
]
},
{
"data": {
"text/plain": [
""
]
},
"execution_count": 26,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"rewrite_graph(grad_y, include=(\"canonicalize\", \"specialize\")).dprint()"
]
},
{
"cell_type": "markdown",
"id": "d492543e",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"#### Back to transformations -- logp inference\n",
"\n",
"Another important graph-to-graph transformation is *automatic logp inference*. PyMC knows how to transform a generatve graph (forward draws) into a logp graph (backwards inference). Let's look at a simple example."
]
},
{
"cell_type": "code",
"execution_count": 27,
"id": "37ed37be",
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"normal_rv{\"(),()->()\"}.1 [id A] 'z'\n",
" ├─ RNG() [id B]\n",
" ├─ NoneConst{None} [id C]\n",
" ├─ [0 0] [id D]\n",
" └─ [1 2] [id E]\n"
]
},
{
"data": {
"text/plain": [
""
]
},
"execution_count": 27,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"import pymc as pm\n",
"\n",
"\n",
"with pm.Model() as model:\n",
" z = pm.Normal(name=\"z\", mu=np.array([0, 0]), sigma=np.array([1, 2]))\n",
"\n",
"pytensor.dprint(z)"
]
},
{
"cell_type": "markdown",
"id": "43b8a6da",
"metadata": {},
"source": [
"We can now use {func}`~pymc.logp` to compute the log-probability of a value."
]
},
{
"cell_type": "code",
"execution_count": 28,
"id": "8e3194d8",
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Check{sigma > 0} [id A] 'z_logprob'\n",
" ├─ Sub [id B]\n",
" │ ├─ Sub [id C]\n",
" │ │ ├─ Mul [id D]\n",
" │ │ │ ├─ ExpandDims{axis=0} [id E]\n",
" │ │ │ │ └─ -0.5 [id F]\n",
" │ │ │ └─ Pow [id G]\n",
" │ │ │ ├─ True_div [id H]\n",
" │ │ │ │ ├─ Sub [id I]\n",
" │ │ │ │ │ ├─ z_value [id J]\n",
" │ │ │ │ │ └─ [0 0] [id K]\n",
" │ │ │ │ └─ [1 2] [id L]\n",
" │ │ │ └─ ExpandDims{axis=0} [id M]\n",
" │ │ │ └─ 2 [id N]\n",
" │ │ └─ ExpandDims{axis=0} [id O]\n",
" │ │ └─ Log [id P]\n",
" │ │ └─ Sqrt [id Q]\n",
" │ │ └─ 6.283185307179586 [id R]\n",
" │ └─ Log [id S]\n",
" │ └─ [1 2] [id L]\n",
" └─ All{axes=None} [id T]\n",
" └─ MakeVector{dtype='bool'} [id U]\n",
" └─ All{axes=None} [id V]\n",
" └─ Gt [id W]\n",
" ├─ [1 2] [id L]\n",
" └─ ExpandDims{axis=0} [id X]\n",
" └─ 0 [id Y]\n"
]
},
{
"data": {
"text/plain": [
""
]
},
"execution_count": 28,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"z_value = pt.vector(name=\"z_value\")\n",
"z_logp = pm.logp(rv=z, value=z_value)\n",
"\n",
"pytensor.dprint(z_logp)"
]
},
{
"cell_type": "markdown",
"id": "942aadb1",
"metadata": {},
"source": [
"Observe that we still get a graph, we do not do any computation yet. To do a evaluation on a given value, we can use the `eval` method:"
]
},
{
"cell_type": "code",
"execution_count": 29,
"id": "1a0f1ff3",
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"Check{sigma > 0}(Sub.0, All{axes=None}.0)"
]
},
"execution_count": 29,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"z_logp.owner"
]
},
{
"cell_type": "code",
"execution_count": 30,
"id": "a6aff350",
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([-0.91893853, -1.61208571])"
]
},
"execution_count": 30,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"z_logp.eval({z_value: [0, 0]})"
]
},
{
"cell_type": "markdown",
"id": "43339908",
"metadata": {},
"source": [
"To \"verify\" the computation, we compute the same quantity using `scipy.stats.norm.logpdf`."
]
},
{
"cell_type": "code",
"execution_count": 31,
"id": "3453b57f",
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([-0.91893853, -1.61208571])"
]
},
"execution_count": 31,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"import scipy\n",
"\n",
"\n",
"scipy.stats.norm.logpdf(\n",
" x=np.array([0, 0]), loc=np.array([0, 0]), scale=np.array([1, 2])\n",
")"
]
},
{
"cell_type": "markdown",
"id": "65c3537c",
"metadata": {},
"source": [
"The values match as expected."
]
},
{
"cell_type": "markdown",
"id": "1e888b20",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"### Composability\n",
"\n",
"It is important to note that all of these transformation operations are *composable*. We already saw an example of this when we applied graph rewrites to a gradient graph. We can also vectorize gradients, or take the gradient of a vectorize graph. Or we can replace subgraphs before or after applying rewrites. Because all of these operations take in a graph and return a graph, we're always able to chain together graph operations. \n",
"\n",
"Sometimes, you'll be surprised by what you end up with:"
]
},
{
"cell_type": "code",
"execution_count": 32,
"id": "f44aed85",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Log [id A]\n",
" └─ Add [id B]\n",
" ├─ ExpandDims{axis=0} [id C]\n",
" │ └─ 1 [id D]\n",
" └─ x [id E]\n"
]
},
{
"data": {
"text/plain": [
""
]
},
"execution_count": 32,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"x = pt.tensor(\"x\", shape=(3,))\n",
"y = pt.log(1 + x)\n",
"y.dprint()"
]
},
{
"cell_type": "markdown",
"id": "fa1eb391",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"The graph we've been working with is $y = \\log(1 + x)$. Let's transform it to be $y = \\log(1 + \\exp(x))$, then rewrite the expression for stability.\n",
"\n",
"First replace $x$ by $\\exp(x)$:"
]
},
{
"cell_type": "code",
"execution_count": 33,
"id": "5dc415eb",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Log [id A]\n",
" └─ Add [id B]\n",
" ├─ ExpandDims{axis=0} [id C]\n",
" │ └─ 1 [id D]\n",
" └─ Exp [id E]\n",
" └─ x [id F]\n"
]
},
{
"data": {
"text/plain": [
""
]
},
"execution_count": 33,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"new_y = graph_replace(y, replace={x: pt.exp(x)})\n",
"new_y.dprint()"
]
},
{
"cell_type": "markdown",
"id": "d418c581",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"Then optimize the graph for stability:"
]
},
{
"cell_type": "code",
"execution_count": 34,
"id": "94ca84f9",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Scalar_softplus [id A]\n",
" └─ x [id B]\n"
]
},
{
"data": {
"text/plain": [
""
]
},
"execution_count": 34,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"rewrite_graph(new_y, include=(\"stabilize\",)).dprint()"
]
},
{
"cell_type": "markdown",
"id": "97e2650b",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"Did you guess the result would be just a single Op?"
]
},
{
"cell_type": "markdown",
"id": "93ed3570-45f3-4df4-bbfd-4ffa0497d30e",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## (3) Compilation\n",
"\n",
"All this is fun and dandy but only useful if we actually use it compute stuff! \n",
"\n",
"PyTensor provides a critical non-composable graph operation: `function`, which converts a pytensor graph into a callable python object that takes concrete inputs and returns concrete outputs. \n",
"\n",
"By default it runs an extensive database of rewrites to try and optimize the computational graph, and then compiles to C (technically a mix of C and Python if not all operations have a C implementation). See https://pytensor.readthedocs.io/en/latest/extending/pipeline.html for a bit more detail.\n",
"\n",
"As with anything remotely useful in Python, when it comes to work you want to [STAY OUT OF PYTHON](https://www.youtube.com/watch?v=vVUnCXKuNOg) as much as possible."
]
},
{
"cell_type": "code",
"execution_count": 35,
"id": "7d74a4d9-2079-4462-81a3-a4c17a271f29",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Cos [id A]\n",
" └─ Squeeze{axes=[0, 1]} [id B]\n",
" └─ Blockwise{dot, (m,k),(k,n)->(m,n)} [id C]\n",
" ├─ ExpandDims{axis=0} [id D]\n",
" │ └─ Exp [id E]\n",
" │ └─ Sin [id F]\n",
" │ └─ x [id G]\n",
" └─ ExpandDims{axis=1} [id H]\n",
" └─ Exp [id E]\n",
" └─ ···\n"
]
},
{
"data": {
"text/plain": [
""
]
},
"execution_count": 35,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"x = pt.vector(\"x\", shape=(None,))\n",
"z = pt.exp(pt.sin(x))\n",
"out = pt.cos((z[None, :] @ z[:, None]).squeeze())\n",
"out.dprint()"
]
},
{
"cell_type": "markdown",
"id": "c9446b3e",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"As noted, use `pytensor.function` to compile a graph into an executable program. You need to pass a **list** of inputs (even if it has no inputs, you still need an empty list!), and outputs (this *can* be a list, but isn't required to be."
]
},
{
"cell_type": "code",
"execution_count": 36,
"id": "c98b61df45d6a2bb",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [],
"source": [
"y_fn = pytensor.function([x], out)"
]
},
{
"cell_type": "markdown",
"id": "5e2727ea",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"What we get back is a `Function` object. This is a wrapper around a call out to a compiled `C` program that now lives in some cache folder somewhere on your computer."
]
},
{
"cell_type": "code",
"execution_count": 37,
"id": "5a8f3eca-51bf-4a3d-a656-85df87135c34",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"data": {
"text/plain": [
"pytensor.compile.function.types.Function"
]
},
"execution_count": 37,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"type(y_fn)"
]
},
{
"cell_type": "markdown",
"id": "b8f7e69c",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"And now we can use it like any other python function"
]
},
{
"cell_type": "code",
"execution_count": 38,
"id": "90f520a5-eec6-42ed-abad-26204cac5868",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"data": {
"text/plain": [
"array(-0.72535991)"
]
},
"execution_count": 38,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"y_fn(np.random.randn(3))"
]
},
{
"cell_type": "code",
"execution_count": 39,
"id": "3badd33e-ddb3-4aca-a27f-49275b1b994b",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"data": {
"text/plain": [
"array(-0.98428505)"
]
},
"execution_count": 39,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"y_fn(np.random.randn(5))"
]
},
{
"cell_type": "markdown",
"id": "c7574ded",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"We can also inspect it to see the final graph that was compiled, after applying rewrites. Notice that `dot` became `CGemv`, so we're using the correct BLAS routine for the inputs provided. It also did some *loop fusion* by compiling a composite inner graph. That is, if we give an array input, rather than looping over it once to compute `exp` of each element, then looping over it again to compute `sin` of each element, we instead loop only once, and compute $\\exp \\circ \\sin$ of each element."
]
},
{
"cell_type": "code",
"execution_count": 40,
"id": "e300df411e0aff49",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Cos [id A] d={0: [0]} 5\n",
" └─ Squeeze{axis=0} [id B] 4\n",
" └─ CGemv{inplace} [id C] d={0: [0]} 3\n",
" ├─ AllocEmpty{dtype='float64'} [id D] 1\n",
" │ └─ 1 [id E]\n",
" ├─ 1.0 [id F]\n",
" ├─ ExpandDims{axis=0} [id G] 2\n",
" │ └─ Composite{exp(sin(i0))} [id H] 0\n",
" │ └─ x [id I]\n",
" ├─ Composite{exp(sin(i0))} [id H] 0\n",
" │ └─ ···\n",
" └─ 0.0 [id J]\n",
"\n",
"Inner graphs:\n",
"\n",
"Composite{exp(sin(i0))} [id H]\n",
" ← exp [id K] 'o0'\n",
" └─ sin [id L]\n",
" └─ i0 [id M]\n"
]
},
{
"data": {
"text/plain": [
""
]
},
"execution_count": 40,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"y_fn.dprint(print_destroy_map=True) # Some memory aliasing optimizations"
]
},
{
"cell_type": "markdown",
"id": "0b4adffa",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"By passing `print_destroy_map=True` to `dprint`, we also get to see where memory buffers are being reused. This shows up in the graph with the line `d={x: [y]}`, where \"x\" is an output, and \"y\" is an input that will be re-used as a buffer. We can see this in two places:\n",
"\n",
"- In the `CGemv` line, we have `d={0: [0]}`. This means that the first output is being allocated to the memory used for the first input. In this case, we save allocation of a length 1 array, which isn't so impressive.\n",
"\n",
"- More interestingly, we see it at the top line, `Cos [id A] d = {0: [0]}`. This means that we are doing the `Cos` directly on the squeezed output of the CGemv operation! This is equivalent to `np.cos(x, out=x)`, which qucikly can become unreadble. "
]
},
{
"cell_type": "markdown",
"id": "5936a640-43ca-4a37-85e5-66feeda4558f",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"PyTensor can also delegate compilation to other libraries in town, namely Numba, JAX, and PyTorch (latter still under active development). \n",
"\n",
"Notice that this is another kind of graph-to-\"graph\" transformation, that we can only do because we have access to the whole static computation. Every individual `Op` knows what it means to become a Numba program, so we can just walk across the graph and generate the appropriate code.\n",
"\n",
"Sometimes, this means that certain rewrites aren't applied! In this case, Numba does it's own BLAS optimizations. So we don't rewrite `dot -> CGemv`, we just leave it as dot."
]
},
{
"cell_type": "code",
"execution_count": 41,
"id": "719fdfbe-790d-41c5-9d4a-398697f01926",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Cos [id A] d={0: [0]} 5\n",
" └─ Squeeze{axes=[0, 1]} [id B] 4\n",
" └─ dot [id C] 3\n",
" ├─ ExpandDims{axis=0} [id D] 2\n",
" │ └─ Composite{exp(sin(i0))} [id E] 0\n",
" │ └─ x [id F]\n",
" └─ ExpandDims{axis=1} [id G] 1\n",
" └─ Composite{exp(sin(i0))} [id E] 0\n",
" └─ ···\n",
"\n",
"Inner graphs:\n",
"\n",
"Composite{exp(sin(i0))} [id E]\n",
" ← exp [id H] 'o0'\n",
" └─ sin [id I]\n",
" └─ i0 [id J]\n"
]
},
{
"data": {
"text/plain": [
""
]
},
"execution_count": 41,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"y_numba_fn = pytensor.function([x], out, mode=\"NUMBA\")\n",
"y_numba_fn.dprint(print_destroy_map=True)"
]
},
{
"cell_type": "code",
"execution_count": 42,
"id": "f9fcb852-49b3-4442-86e8-eccab65f3834",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"CPU times: user 98 ms, sys: 8.58 ms, total: 107 ms\n",
"Wall time: 110 ms\n"
]
},
{
"data": {
"text/plain": [
"array(-0.97979355)"
]
},
"execution_count": 42,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"%%time\n",
"\n",
"y_numba_fn(\n",
" np.random.randn(3)\n",
") # first time takes long, jit compilation actually happening"
]
},
{
"cell_type": "code",
"execution_count": 43,
"id": "b007790d-fa14-4ac4-823e-94cf2df15e35",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"CPU times: user 136 μs, sys: 71 μs, total: 207 μs\n",
"Wall time: 243 μs\n"
]
},
{
"data": {
"text/plain": [
"array(0.99905205)"
]
},
"execution_count": 43,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"%%time\n",
"\n",
"y_numba_fn(np.random.randn(5))"
]
},
{
"cell_type": "markdown",
"id": "eab1d41c",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## A Full Example: Logistic Regression with Gradient Descent\n",
"\n",
"To show everything in action together, let's look at how we would write a binary classification model, how we can train it using gradient descent, and how we can use the final program we get back.\n",
"\n",
"First, let's set up the symbolic inputs. These will be the input data $X$ and targets $y$, as well as the initial values for alpha and beta. Our model will be:\n",
"\n",
"$$ p = \\sigma^{-1}(\\alpha + X \\beta) $$\n",
"\n",
"Where $\\sigma$ is the logistic function.\n",
"\n",
"And we'll choose parameters $\\alpha$ and $\\beta$ to minimize the binary cross entropy between $p$ and the target labels, which will just be:\n",
"\n",
"$$\\mathcal{L} = -\\frac{1}{N} \\sum_{i=0}^N y_i \\log(p_i) + (1 - y_i) \\log(1 - p_i)$$\n",
"\n",
"If there are any Bayesians in the audience, you will also recognize this as the negative log-likelihood of a Bernoulli GLM"
]
},
{
"cell_type": "code",
"execution_count": 44,
"id": "e448cd31",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [],
"source": [
"X_pt = pt.tensor(\"X\", shape=(None, None))\n",
"y_pt = pt.tensor(\"y\", shape=(None,))\n",
"alpha_pt = pt.tensor(\"alpha\", shape=())\n",
"beta_pt = pt.tensor(\"beta\", shape=(None,))\n",
"\n",
"p = pt.sigmoid(alpha_pt + X_pt @ beta_pt)\n",
"p.name = \"p_class_0\"\n",
"\n",
"loss = -(y_pt * pt.log(p) + (1 - y_pt) * pt.log(1 - p)).mean()\n",
"loss.name = \"cross_entropy\""
]
},
{
"cell_type": "markdown",
"id": "eb622fa5",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"To convince you that the text version of dprint is nicer, here's the big graphic plot for our loss function:"
]
},
{
"cell_type": "code",
"execution_count": 45,
"id": "d52561b6",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"data": {
"image/svg+xml": [
""
],
"text/plain": [
""
]
},
"execution_count": 45,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"SVG(pydotprint(loss, return_image=True, format=\"svg\"))"
]
},
{
"cell_type": "markdown",
"id": "77b258df",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"Comparsed to the text verison. It pays dividends to get used to reading these things!"
]
},
{
"cell_type": "code",
"execution_count": 46,
"id": "e793a2bc",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Neg [id A] 'cross_entropy'\n",
" └─ True_div [id B] 'mean'\n",
" ├─ Sum{axes=None} [id C]\n",
" │ └─ Add [id D]\n",
" │ ├─ Mul [id E]\n",
" │ │ ├─ y [id F]\n",
" │ │ └─ Log [id G]\n",
" │ │ └─ Sigmoid [id H] 'p_class_0'\n",
" │ │ └─ Add [id I]\n",
" │ │ ├─ ExpandDims{axis=0} [id J]\n",
" │ │ │ └─ alpha [id K]\n",
" │ │ └─ Squeeze{axis=1} [id L]\n",
" │ │ └─ Blockwise{dot, (m,k),(k,n)->(m,n)} [id M]\n",
" │ │ ├─ X [id N]\n",
" │ │ └─ ExpandDims{axis=1} [id O]\n",
" │ │ └─ beta [id P]\n",
" │ └─ Mul [id Q]\n",
" │ ├─ Sub [id R]\n",
" │ │ ├─ ExpandDims{axis=0} [id S]\n",
" │ │ │ └─ 1 [id T]\n",
" │ │ └─ y [id F]\n",
" │ └─ Log [id U]\n",
" │ └─ Sub [id V]\n",
" │ ├─ ExpandDims{axis=0} [id W]\n",
" │ │ └─ 1 [id X]\n",
" │ └─ Sigmoid [id H] 'p_class_0'\n",
" │ └─ ···\n",
" └─ Subtensor{i} [id Y]\n",
" ├─ Cast{float64} [id Z]\n",
" │ └─ Shape [id BA]\n",
" │ └─ Add [id D]\n",
" │ └─ ···\n",
" └─ 0 [id BB]\n"
]
},
{
"data": {
"text/plain": [
""
]
},
"execution_count": 46,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"loss.dprint()"
]
},
{
"cell_type": "markdown",
"id": "33a6398f",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"To compute an update step, we will use a simple gradient descent algorithm, defined as:\n",
"\n",
"$$\\theta^\\prime = \\theta - \\eta \\nabla \\mathcal{L}(\\theta)$$"
]
},
{
"cell_type": "code",
"execution_count": 47,
"id": "d24ad49c",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [],
"source": [
"# The learning rate is another root variable we need to provide\n",
"eta_pt = pt.tensor(\"learning_rate\", shape=())\n",
"\n",
"\n",
"# We can compute gradients for a list of varibales too!\n",
"# It's also good to apply some graph simplification before taking gradients. PyMC does this\n",
"# by default, for example.\n",
"d_alpha, d_beta = grad(\n",
" rewrite_graph(loss, include=(\"canonicalize\", \"stabilize\")), wrt=[alpha_pt, beta_pt]\n",
")\n",
"\n",
"# Apply gradient updates\n",
"alpha_prime = alpha_pt - eta_pt * d_alpha\n",
"beta_prime = beta_pt - eta_pt * d_beta"
]
},
{
"cell_type": "markdown",
"id": "7e963af4",
"metadata": {},
"source": [
"Compile our functions. We can make one for training, and one for prediction. Here we see another example of a PyTensor superpower: we don't have to know ahead of time how we want to use different outputs. We do all the steps of computation symbolically, then only at the end decide what will be used where. This type of thinking ahead is especially important when you're writing programs in Numba. You will need to think about what units of computation can be decomposed and jitted, for reuse in later jitted functions. We see that PyTensor does this reasoning for us.\n",
"\n",
"\n",
"Getting to this point, we realized that we can output class probabilities, but not class labels. It's easy to make one more root variable for the prediction function, representing a prediction threshold for membership in class 1. Then we can make a `y_hat` variable and return it."
]
},
{
"cell_type": "code",
"execution_count": 48,
"id": "10903335",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [],
"source": [
"training_fn = pytensor.function(\n",
" [X_pt, y_pt, eta_pt, alpha_pt, beta_pt], [loss, alpha_prime, beta_prime]\n",
")\n",
"\n",
"threshold = pt.tensor(\"threshold\", shape=())\n",
"y_hat = (p > threshold).astype(int)\n",
"predict_fn = pytensor.function([X_pt, alpha_pt, beta_pt, threshold], [p, y_hat])"
]
},
{
"cell_type": "markdown",
"id": "1480f470",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"It's worth having a look at the dprint of `training_fn` to see a couple features of pytensor we haven't run into yet.\n",
"\n",
"1. Sub-computations are automatically re-used! The first output, `Composite{...}.1 [id A] 9` is the cross entropy. It gets computed once (it's the first return, after all), but then it is also used in the 2nd return, to compute `alpha_prime`.\n",
"2. `Composite{...}.0 [id I] 4` is the probability of class 0. That also gets computed once and re-used several times.\n",
"3. Unused computations get truncated! Notice that `p_class_0` never appears as such. Instead, we got a composite sub-graph that compute that quantity given inputs. The thing itself was never requested, and is thus never used."
]
},
{
"cell_type": "code",
"execution_count": 49,
"id": "5e899f55",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Composite{...}.1 [id A] 'cross_entropy' d={0: [1]} 9\n",
" ├─ Assert{msg='Could not broadcast dimensi...'} [id B] 8\n",
" │ ├─ Shape_i{0} [id C] 0\n",
" │ │ └─ X [id D] \n",
" │ └─ Eq [id E] 7\n",
" │ ├─ Shape_i{0} [id C] 0\n",
" │ │ └─ ···\n",
" │ └─ Shape_i{0} [id F] 6\n",
" │ └─ y [id G] \n",
" └─ Sum{axes=None} [id H] 5\n",
" └─ Composite{...}.0 [id I] d={0: [1]} 4\n",
" ├─ ExpandDims{axis=0} [id J] 3\n",
" │ └─ alpha [id K] \n",
" ├─ CGemv{inplace} [id L] d={0: [0]} 2\n",
" │ ├─ AllocEmpty{dtype='float64'} [id M] 1\n",
" │ │ └─ Shape_i{0} [id C] 0\n",
" │ │ └─ ···\n",
" │ ├─ 1.0 [id N] \n",
" │ ├─ X [id D] \n",
" │ ├─ beta [id O] \n",
" │ └─ 0.0 [id P] \n",
" └─ y [id G] \n",
"Composite{(i2 - (i0 * i1))} [id Q] d={0: [1]} 13\n",
" ├─ learning_rate [id R] \n",
" ├─ Sum{axes=None} [id S] 12\n",
" │ └─ Composite{((i2 / i1) + (i0 / i1))} [id T] d={0: [0]} 11\n",
" │ ├─ Composite{...}.1 [id I] d={0: [1]} 4\n",
" │ │ └─ ···\n",
" │ ├─ ExpandDims{axis=0} [id U] 10\n",
" │ │ └─ Composite{...}.0 [id A] d={0: [1]} 9\n",
" │ │ └─ ···\n",
" │ └─ Composite{...}.2 [id I] d={0: [1]} 4\n",
" │ └─ ···\n",
" └─ alpha [id K] \n",
"CGemv{no_inplace} [id V] 16\n",
" ├─ beta [id O] \n",
" ├─ Neg [id W] 15\n",
" │ └─ learning_rate [id R] \n",
" ├─ Transpose{axes=[1, 0]} [id X] 'X.T' 14\n",
" │ └─ X [id D] \n",
" ├─ Composite{((i2 / i1) + (i0 / i1))} [id T] d={0: [0]} 11\n",
" │ └─ ···\n",
" └─ 1.0 [id N] \n",
"\n",
"Inner graphs:\n",
"\n",
"Composite{...} [id A] d={0: [1]}\n",
" ← Cast{float64} [id Y] 'o0'\n",
" └─ i0 [id Z] \n",
" ← neg [id BA] 'o1'\n",
" └─ true_div [id BB] \n",
" ├─ i1 [id BC] \n",
" └─ Cast{float64} [id Y] 'o0'\n",
" └─ ···\n",
"\n",
"Composite{...} [id I] d={0: [1]}\n",
" ← add [id BD] 'o0'\n",
" ├─ mul [id BE] \n",
" │ ├─ -1.0 [id BF] \n",
" │ ├─ i2 [id BG] \n",
" │ └─ scalar_softplus [id BH] \n",
" │ └─ neg [id BI] 't11'\n",
" │ └─ add [id BJ] 't3'\n",
" │ ├─ i0 [id BK] \n",
" │ └─ i1 [id BL] \n",
" └─ mul [id BM] \n",
" ├─ -1.0 [id BF] \n",
" ├─ sub [id BN] 't14'\n",
" │ ├─ 1.0 [id BO] \n",
" │ └─ i2 [id BG] \n",
" └─ scalar_softplus [id BP] \n",
" └─ add [id BJ] 't3'\n",
" └─ ···\n",
" ← mul [id BQ] 'o1'\n",
" ├─ sub [id BN] 't14'\n",
" │ └─ ···\n",
" └─ sigmoid [id BR] \n",
" └─ add [id BJ] 't3'\n",
" └─ ···\n",
" ← mul [id BS] 'o2'\n",
" ├─ -1.0 [id BF] \n",
" ├─ i2 [id BG] \n",
" └─ sigmoid [id BT] \n",
" └─ neg [id BI] 't11'\n",
" └─ ···\n",
"\n",
"Composite{(i2 - (i0 * i1))} [id Q] d={0: [1]}\n",
" ← sub [id BU] 'o0'\n",
" ├─ i2 [id BV] \n",
" └─ mul [id BW] \n",
" ├─ i0 [id BX] \n",
" └─ i1 [id BY] \n",
"\n",
"Composite{((i2 / i1) + (i0 / i1))} [id T] d={0: [0]}\n",
" ← add [id BZ] 'o0'\n",
" ├─ true_div [id CA] \n",
" │ ├─ i2 [id CB] \n",
" │ └─ i1 [id CC] \n",
" └─ true_div [id CD] \n",
" ├─ i0 [id CE] \n",
" └─ i1 [id CC] \n"
]
},
{
"data": {
"text/plain": [
""
]
},
"execution_count": 49,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"training_fn.dprint(print_type=True, print_destroy_map=True)"
]
},
{
"cell_type": "markdown",
"id": "6c880ffa",
"metadata": {},
"source": [
"The last point about truncation is even more clear when we look at the graph for `predict_fn`. Now the loss is nowhere to be seen! We just compute exactly what was requested.\n",
"\n",
"Note that we also have a nice example of re-using computation. We compute `p_class_0` exactly once, then re-use it in the 2nd output."
]
},
{
"cell_type": "code",
"execution_count": 50,
"id": "1a50f419",
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Composite{...}.0 [id A] 'p_class_0' 5\n",
" ├─ ExpandDims{axis=0} [id B] 4\n",
" │ └─ alpha [id C] \n",
" ├─ CGemv{inplace} [id D] 3\n",
" │ ├─ AllocEmpty{dtype='float64'} [id E] 2\n",
" │ │ └─ Shape_i{0} [id F] 1\n",
" │ │ └─ X [id G] \n",
" │ ├─ 1.0 [id H] \n",
" │ ├─ X [id G] \n",
" │ ├─ beta [id I] \n",
" │ └─ 0.0 [id J] \n",
" └─ ExpandDims{axis=0} [id K] 0\n",
" └─ threshold [id L] \n",
"Composite{...}.1 [id A] 5\n",
" └─ ···\n",
"\n",
"Inner graphs:\n",
"\n",
"Composite{...} [id A]\n",
" ← sigmoid [id M] 'o0'\n",
" └─ add [id N] \n",
" ├─ i0 [id O] \n",
" └─ i1 [id P] \n",
" ← Cast{int64} [id Q] 'o1'\n",
" └─ GT [id R] \n",
" ├─ sigmoid [id M] 'o0'\n",
" │ └─ ···\n",
" └─ i2 [id S] \n"
]
},
{
"data": {
"text/plain": [
""
]
},
"execution_count": 50,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"predict_fn.dprint(print_type=True)"
]
},
{
"cell_type": "markdown",
"id": "615f13ef",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"### Training"
]
},
{
"cell_type": "code",
"execution_count": 51,
"id": "b57e8e42",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [],
"source": [
"import numpy as np\n",
"from sklearn.datasets import make_classification\n",
"\n",
"\n",
"seed = sum(map(ord, \"I <3 Pytensor\"))\n",
"rng = np.random.default_rng(seed)\n",
"\n",
"X, y = make_classification(\n",
" n_samples=100,\n",
" n_features=5,\n",
" n_redundant=0,\n",
" n_informative=5,\n",
" n_classes=2,\n",
" random_state=seed,\n",
")\n",
"\n",
"# Initial values for parameteres\n",
"beta = rng.normal(0, 1, size=(5,))\n",
"alpha = rng.normal(0, 1)\n",
"\n",
"learning_rate = 1e-1"
]
},
{
"cell_type": "code",
"execution_count": 52,
"id": "f4400eb1",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [],
"source": [
"n_steps = 1_000\n",
"histories = [np.empty(n_steps), np.empty(n_steps), np.empty((n_steps, 5))]\n",
"\n",
"for t in range(n_steps):\n",
" loss_val, alpha, beta = training_fn(X, y, learning_rate, alpha, beta)\n",
" histories[0][t] = loss_val\n",
" histories[1][t] = alpha\n",
" histories[2][t] = beta"
]
},
{
"cell_type": "code",
"execution_count": 53,
"id": "58052478",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABlcAAAfnCAYAAABGED7UAAAAOnRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjEwLjUsIGh0dHBzOi8vbWF0cGxvdGxpYi5vcmcvWftoOwAAAAlwSFlzAAAewgAAHsIBbtB1PgABAABJREFUeJzs3QmYXGWVP+DTeyedhCQQEkjYIWEJCMimjqCITlzZBkUERAHFBQURhhm3QRSRPyiCiCKIbKIijOIgoAgoiMAwgCir7EsIhOx7r//nu9BNd7q601Vd3ZWuel+feqr61q1bX1V17oP163NOVUdHR0cAAAAAAAAwINUD2w0AAAAAAIBEuAIAAAAAAJAH4QoAAAAAAEAehCsAAAAAAAB5EK4AAAAAAADkQbgCAAAAAACQB+EKAAAAAABAHoQrAAAAAAAAeRCuAAAAAAAA5EG4AgAAAAAAkAfhCgAAAAAAQB6EKwAAAAAAAHkQrgAAAAAAAORBuAIAAAAAAJAH4QoAAAAAAEAehCsAAAAAAAB5EK4AAAAAAADkQbgCAAAAAACQB+EKAAAAAABAHmrz2RkAACrJ3nvvHS+88MKwPd/+++8fp59+eoxUd911Vxx++OEj6rUddthhcffdd+e8749//GNMmzZt2NcEAACs/VSuAAAAAAAA5EG4AgAAAAAAkAfhCgAAAAAAQB6EKwAAAAAAAHkw0B4AAPrwlre8JebNm7fG/RYsWBD33ntvn/e/4x3vGNDzbbvttnmtDwAAgNKo6ujo6CjRcwMAQFm466674vDDD+/z/kcffXRY1wMAAMDQ0hYMAAAAAAAgD8IVAAAAAACAPJi5AgAAI9ATTzwR9913X7zyyisxduzYmD59euy4445RV1e3xseuWrUqe3y6LFq0KJYtWxbt7e3R2NiYHWvKlCmx1VZbxeTJk2NtlNabZtw89dRTsXz58lhnnXWyte6yyy4xbty4WBul9/rvf/97vPzyy1FTUxPrrbdebLnllrHddtsV7TlS+7l//vOfMXfu3GhpaYn1118/+53YdNNNi/YcAADAq4QrAACwFtl7773jhRde6LX9mGOOieOPPz5eeuml+M///M+4/fbbe+2TgoU0++XYY4/Neez0mJ///Ofx5z//OQtY1mTatGnx/ve/Pz760Y/GhAkTBjV7Zv/994/TTz89533XXHNN/Md//EfO+x588MGorX31/7Y899xz8YMf/CCuu+66nOtPwdIee+wRn/3sZ7NQYSAOO+ywuPvuu3Pe98c//jF7Dwr5nJI03jK9tosuuigLV3LZYIMN4qCDDoqPf/zjMWrUqMhXc3NzXHzxxXHVVVdl708u22+/ffY7sddee2U/L168OHbdddec+37rW9+KAw44IO91AABApdEWDAAARohUkXDIIYfkDFY6vzSfPXt2r+1Lly6NT3/603HkkUfGH/7whwEFK8nzzz8f559/frzrXe+KG264IUrpl7/8ZRb0pLCir/Wnao3bbrstPvShD8U3v/nNLNwo5Wd16KGHZkFYX8FK8uKLL8Y555wTs2bNyipP8nH//ffHe97znvjOd77TZ7CSpIqZT3ziE/HVr341Wltb83oOAAAgN+EKAACMAOlL8VSRkQKP/qQKke5S26xUTZKqMAqVQpvjjjsuqxgphXPPPTe+8pWvxIoVKwb8mEsvvTS+/e1vRymkipYU8Nxzzz0DfsycOXOyz2lNn2+nP/3pT3HEEUf0G6qs7he/+EV84QtfyFrAAQAAgyNcAQCAESC1fUqVCv3ZaKONerV7+q//+q+stdZgpSqQr33ta1kVzHBKgcD3v//9gh57ySWXFOW15zsPJlUI5WoZtiYLFy7M2nKtyWOPPZa1+conbOp04403xve+9728HwcAAPQkXAEAgBEgDZ5fk/322y+qqqq6fk4D73/zm98UbQ1LlizJ2ooNp4GEDX1JFRpXXnllDKc00+app54q+PGpwihVsfQ3Y+WEE04YcGu3XH72s58V/FgAAOBVBtoDAMAIs+2222ZD5jfZZJOYN29eFnikll0pXOnuRz/6UZ/HmDRpUta6aocddoiJEydmX9anllS33nprNl+lr3klKbBZvfXYUEpzVLpX5nz4wx+OrbbaKkaPHp3NKEnVKc8880yfj7/llltiOHVfb01NTbz73e+Ot73tbTFt2rSsMuX3v/99Fni1tbXlfHx639Oa0+vMJT02Va70Z88994z3ve992e9Hqm5JM1fSzJp8WogBAAD9E64AAMAI8va3vz3OO++87Iv7Tvvss08cf/zxMWXKlK5t6Yv8NNw9l6lTp2ZtxtZdd90e23fZZZcsoPnxj38cZ555Zs7HFtLuqhjSPJKTTz65x+tO6913333jYx/7WDzwwAM5H/fKK69k78X48eOHcbUR66+/fvY+br311r0+v7e+9a3Z59WXJ554os/7Lr/88j7vq6ury+bMvPe97+2x/U1velMWxqW5NcWsZAIAgEqmLRgAAIwQ6cvzNPeke8DQqXuwklRXV8c3v/nN+PjHPx5vfvObs+qUTv/5n//ZK1jp7tBDD82eK5dUKTPcUhXGl770pZyve8yYMdlcmf7MnTs3hlNtbW1cfPHFvYKVTu95z3uykKUvL7/8cs7tjz/+eDzyyCN9Pu7EE0/sFax0amhoyIKXPfbYY43rBwAA1kzlCgAAjBCpAmGDDTYY0L7jxo3r1SYsfWmfWkqlsKU/o0aNysKYl156qdd9K1eujOGUQqLjjjuu33222267mDx5cs71dg6ZH04f+MAHYsstt+x3n3e84x19tizra72pJVtfUjXSYYcd1u9zpnk8X/7yl7OwCgAAGByVKwAAMEIMtuogtar6l3/5lyyw6Esapn7FFVdkw+v7Gqg+nFJIkWatrEl/+3SfgzIc0oyVNUkzWPJdb1+tz5I026W/z7VTmleTwigAAGBwVK4AAMAIsfnmmxf1eOlL/NRq6h//+Efcf//9ce+998aTTz4Za5M0lH2glTp9aW9vj7Vtzeuss06f96Wh9rnMnj27z8dsv/32A1xdxBve8IZ48MEHB7w/AADQm3AFAABGiFR5Mhippdcdd9wRd955ZxamPPzww8NeiZKv/mbDdDd69OhYW6y33npr3Ce1XsvX4sWL+7xv9Zk7hVbNAAAAAyNcAQCAEaK/aof+PPvss/GDH/wgbrjhhlixYkWMJGlg/UDkGna/Nq85Db0vZrjS1NQ04OOMHTs27+cGAAB6Eq4AAMAIkc8X6J0uv/zyOPPMMwccqqSh59OnT88CmbUhiBloCDGQeSNr05rT+5yv/l7jqlWrBnyctb1aCQAARgLhCgAAjBCNjY157X/VVVfFqaeeusZ2Wmlex4477pjN4thpp51i4sSJsffee8cLL7wQpVZIhUe5rrm/ipP+qlpWt3DhwiKtCAAAKtfI+38qAABQoerq6ga871NPPRWnnHJKn/fPmjUrPvShD8Uuu+wS9fX1ve5va2sreJ0MjRR69eWxxx6LN7/5zQM6zkMPPVTEVQEAQGVae2rnAQCAos0VSe3AWlpact533HHHxfe+973sy/hcwUq+baYYHltvvXWf991xxx0DOsby5cvjrrvuKuKqAACgMglXAABghMhnTsftt9/eZxuwo446ao0zORYtWpT3+hhaO+ywQ7+f99NPPz2g0G3p0qVFXhkAAFQe4QoAAJSh2bNn59ze0NCwxvZit956a7S3t+e8r6/tDL1UaTRmzJic96U2bv/+7/+eVab05c4774xzzjlnCFcIAACVQ7gCAABlqK+h6gsWLIh77723z8fNmzcvzjrrrH6rWiiNxsbGbFZOX+6///447LDDes1USYHLBRdcEEcffXSfreIAAID8GGgPAABlaMqUKfHkk0/mvO+kk06K8847L2bMmNFj+z333BNf+tKX+m0vtWzZsqKvlYE75phj4tprr+0z5PrHP/4R+++/f2y++eYxderUrAXYww8/HCtXrhz2tQIAQDkTrgAAQBl6y1ve0me48txzz8UBBxwQb33rW7Mv4dPw+hSsPPLII2s8bvqSPn1h31d7KobWRhttFEceeWScf/75/e6XPvu+Pv9UASNsAQCAwdEWDAAAytChhx7a72yV1tbWuOWWW+Kiiy7KhpwPJFjp1NeX9gyPz372s7HbbrsV9Nitt946PvKRjxR9TQAAUGmEKwAAUIY23XTTOO644wp67Lhx4+KEE07o8/6//vWvg1gZxZinkypXdtlll7weN3369CxMGzVqVJ/7VFf7v4gAADAQ/ssZAADK1FFHHRXHHntsXl+Yb7PNNvGLX/wiG34+adKknPv8/ve/L+IqKURqy/bTn/40m8HSX4VSp9QG7sorr4z11luv3/0GciwAAEC4AgAAZd9C6rLLLot/+Zd/iaqqqj7323bbbePb3/52XHPNNdkclrTvO97xjj6HpqcLpZWCkOOPPz7++Mc/ZlVKu+66a0yYMCGrbEnVKalS5bDDDotrr702vvWtb3XNyeno6OjzmA0NDcP4CgAAYOSq6ujvv6wBAICyMX/+/LjvvvvixRdfjCVLlsTYsWOz6pQdd9wxJk+eXOrlMUzOPPPM+PGPf5zzvjR/J4U0AABA/2rXcD8AAFAmJk6c2Gc1CiPD1VdfHVOmTMkuKRDrrEbJxyuvvNLnfWtqGwYAALxK5QoAAMAIsd1220Vra2vXzylc6QxbUju3L33pS/0+vrm5Od71rndl1Uu52ozdf//9WVsxAACgf2auAAAAjBDrrrtuj5+XLl0ajz/+eNx+++1x6aWXxr333tvnY9vb27PZK7mClc65O4IVAAAYGP/lDAAAMELMnDkzXnrppT7v/+QnPxmHHnpovPGNb4zx48dngUqatfPoo4/Gddddl133JVW0AAAAA6MtGAAAwAhxww03xOc///miH3f06NHxpz/9KcaNG1f0YwMAQDnSFgwAAGCE+Nd//dfYZZddin7cz3zmM4IVAADIg3AFAABghKiqqorvfOc7sckmmxTtmO95z3viqKOOKtrxAACgEghXAAAARpDJkyfH5ZdfHvvss8+gjlNXVxdf/OIXs7AGAADIj5krAAAAI9T//u//xrXXXhs33XRTNrh+IDbeeOPYd9994+CDD4711ltvyNcIAADlSLgCAABQBl566aV4/PHHY86cObFs2bJYsWJFtLa2Rn19fYwfPz6mTJkS06dPzypfAACAwRGuAAAAAAAA5MHMFQAAAAAAgDwIVwAAAAAAAPIgXAEAAAAAAMiDcAUAAAAAACAPwhUAAAAAAIA8CFcAAAAAAADyIFwBAAAAAADIg3AFAAAAAAAgD8IVAAAAAACAPAhXAAAAAAAA8iBcAQAAAAAAyINwBQAAAAAAIA/CFQAAAAAAgDwIVwAAAAAAAPIgXAEAACgTLS0tpV4CAABUBOEKAADACDdnzpz49Kc/Hffee2+plwIAABVBuAIAADCCXXfddfHud787/vjHP5Z6KQAAUDGEKwAAACPYbbfdFsuXLy/1MgAAoKIIVwAAAAAAAPIgXAEAAAAAAMiDcAUAAAAAACAPVR0dHR35PAAAAFi7Pfzww3HVVVfF3XffHc8//3y0trbGuuuuG294wxtiv/32i7333rvH/nfddVccfvjh2e3vfOc78Y53vCO++93vxm9/+9tYsWJFbLjhhvEv//IvcdJJJ0VNTU3X49rb2+P3v/99/O53v4u///3vMW/evKitrY31118/dtttt9h///1jp512WuN677///rjmmmvinnvuiRdffDHa2tpi/PjxseWWW2bP+2//9m8xbty4Ph/f3NycrfUPf/hD/OMf/4iFCxdGQ0NDrLfeetnzv+td7+r1mgcr/d+oG2+8Ma6//vp44IEHstdeX18fG2ywQeyxxx5x8MEHxxZbbNHn408++eT47//+7+wx6b1L7+W1116bvY7HHnssFixYkL0H6TNL7+M+++zT6xiHHXZY9hn35dJLL43dd989uz1jxozs+kMf+lB8/etfjyuvvDIuvvjimDNnTvY+7bLLLvH5z38+pk6d2uMYf/vb3+JXv/pV9tmkfdNnk/afOXNmzJo1K7tUV+f+m73uv1ff+ta34oADDsjWe8kll2TvWedr3GGHHbLPONdn9MQTT8R73vOe7PaoUaPijjvuiNGjR0d//uu//it7fcnZZ58d7373u/vdHwAACiFcAQCAMrFy5co45ZRTsqCiP3vuuWcWnowZMyZnuPI///M/cfPNN/d4zHbbbdfjuI8//niccMIJ8cgjj/T7XOmL7W9+85vR1NTU6770Rf2pp57a9UV4X1Kw8u1vfzvnl+/PPfdcfOITn4gnn3yy32PsuOOOcf7558fEiRNjsF544YUsiEihSF9SCPWxj30se49yhQ/dw5U///nPceyxx8b//u//9nm89Nq/973vZfsPNlzZbLPN4vTTT++xb11dXfzlL3+JddZZJ/t50aJF8dWvfjVuuOGGft+LrbfeOlvXpptuusZwJQVn5557bhZM5ZJCsLPOOqvHa0wOPPDALDRL0v3ve9/7+lxPS0tLFsilgC393qTXtPrxAACgGGqLchQAAKCkUlDx6U9/OvsyuVOq2th1112zL5dTCJICk1Qhkb7M/8xnPpNVLqz+xX/6wv+2227rdfxUodA9WDnkkEOyL+A7Kwre9ra3xVZbbZVVkdx3333ZF+tJqux49tln44orrsj26+5HP/pRV7CSvtx/+9vfnh0j3U5fxKdKlPnz58fixYvjc5/7XPzmN7/pUQ2SnuuYY47pClZS1UhaR7pevnx5VgFy6623Zq85Vcd89rOfjZ/97GeDep9TmPPhD3845s6dm/2cKi/SujfZZJMs3EoVGX/961+zz+PCCy/M9jvjjDP6PF4KGtLndu+990ZjY2MWoqSKnXSs9DmkKqQkfXYpmEhhTae0jvR6U+VQZ/iQKmY23njj7HbndXfPPPNMzvAtVdt0BivLli2Lj3/8413HrKqqykKaFFClz+af//xn9r6mNabfqw9+8IPZ59hfpU76veoMgjbffPPsdabfh/S53H777dn7kKqgUlD2k5/8pMfvZarc6VxLCv76C1fSe5aClc7fWcEKAABDRbgCAABl4Kc//WlXsJLaJqW/8F+90iN98X/EEUdkX57feeedWViRvrhe/cvp1NrrxBNPzFqIpZAgfbH/5je/uasyIAUzncFKCnBS66UpU6b0OE76Ij0FIqn104MPPphVqJx22mld96cv5i+66KKu9aYqi+23375XdcenPvWpbK3peVNYkSogOqW2XCnoSVIbsnR/age2+mv+6Ec/moUt//d//5dVh6TAqRDpvTj++OO7gpX3v//9WQuqzgqg7s+ZgpyXXnope49TMJGqL3JJrysFK+l9TBUgkydP7rovBSnpvU0VN8nll1+eVbh0Bgad7bJS2NEZPqRtndUquaT3MkktutLnmMKh9L50DyHSZ9V5vNQC7Jxzzok3vvGNvap30ueb9ku/C+n1ptfaV5jRGaykMCw9rnt7udTqKz0+/V6mYCq1IUuBTaf3vve9WaVNeq9SEJOerzMIWl1qq9Zp33337fN9AACAwTLQHgAARrhUmdEZVCTpi+hcLbTSbIvU6qnTL37xi5zHS19+pxAmffGeZrUcdNBBXbM4UtXD008/nd1O21KgsXqw0hl2pMqUFNR0Vi50b92VZmksXbo0u/2mN72pV7DSGbp84xvf6Po5hTSrzwPplAKU1YOVztecqjCSVA2Rgo9CpTCnsxVYqvRIFSmrByudz/n9738/q/hIzjvvvCyY6UtqX/XDH/6wR7DS/bPorEBJAdFg1t8ptc1KIdW0adOy9e+1117ZZ9D5uaSQJElVKhdccEGvYKXzs0+VT6lKKEmf7a9//et+nze1JEvhVPdgJUnBXfc2ZSlk6v5+TZgwIWtll6SAJX0OuaTfp852dml9udYNAADFIlwBAIARLrXhSgPVO2dr/Ou//muf+6bKhm233Tbe+ta3Zm2eVp9/kQKB1G6qL6ktU6dUbZArXOiUhrF3VlekACgFLJ26f8Ge2nelqoVcNtpoo2zQe6o4SdfddT9Geg/6kuZ+pNkhKYw58sgjo1CpoqJTal/V1yD3zoDlLW95S1eVR6oO6W8uTQqycknPkYbNd+qsmhmM1NKtL6nFWPqsktR+K83a6S8UStUvna6++uo+903B1xe+8IU+70/zVtL8luSVV17p9Xl2r7Dq/jvYXWojlyqikg984ANd4RYAAAwF4QoAAIxwqa1SpzSDoz+pbVMKOVLFSWq7tfoX0GluRvrSPJdVq1Z1femdHpe+EF+TFBx06j6wPc3dSFUxnXNMUtusNA8lBRGrS4FRrjV1b++VXs9xxx0Xt9xyS1bh0V1qIZWGuA9m/kZra2uPL/xTQLUmqdVXp/7ClRRC9SdVbnT/DAar+7r6ahuWDOTzTXNNOn+HUouwFStW5NwvVaf0FSB16l5ttfrcn1Rd0/n49Hv08ssv93q8lmAAAAwnM1cAAGCES8PfO6Vh6IORWkX1Jc0QSW2ZOvfrr2ql0zbbbNN1+/nnn++6nYKOVMnwpS99Kfv5qaeeilNOOSW7nYKQ1LoqVdek9lu52n11fhmf2o91zvO4/vrrs0tqZ7Xzzjtnx0hh0/Tp02OwZs+e3SO0Sesq9DNaXZpr0p80+L3T6pVG+Uqt1iZOnNjn/d0/o+6fXV/Gjh2b/S6kgCwFUOl1puBsdTNnzlzjsbbaaqse73d36fclVUGlAC5V1qQKm9S6rntFT2cwlMKq9DsEAABDSbgCAAAj3Pz587tu9zXoe6DSl+V9WbhwYd7P071aofvjk3/7t3/Lqh6+/e1vZ0PKO6WgJV0uu+yyaGpqin322SeOPvroHl++d7bM+sEPfpDNZUlzQjqDhxQA3XXXXdnlrLPOik022SQb4J7ag6VwoVMaJN9fO7HOKo8U1Ky+9nz19/jGxsYBH2ew4Up/n+9gPuMUriTdP8fu+gt0OnWvTupsc7d6a7AUriTXXXddj3Al/dw5p0XVCgAAw0G4AgAAI1xnNUkxdA6gL9YX+90Hk+eagZHagaXWYWlexh//+Mf4y1/+0jXoPkmzWFJwkr48/9rXvhYf/OAHe4UFKZxJsz/SPqktWBo63zk3JHnmmWfiu9/9bvzyl7+MSy+9tKs6Jz1XGjzfnzRXJoUr3V9Hes5PfepTeb0PKeBZG/T3+Rb6GXd/r/uac5Kqidak+3uca/80xyZVxTz55JPxwAMPxLPPPhsbb7xxdl/nPJ70uO6t6AAAYKgIVwAAYITr/hf/ixcvHpbnGWglx4IFC3I+vrtUTZKqDdIlfcH+4IMPxl//+tf405/+lFWXpC/8U8up//qv/4rdd989Z1CRvmRPgUe6pPcgtQpLs2hS2NLZYirNc0lzZi6//PJBvfa0niOPPDLKUXqdqcVW52fcvdJnIJ9xX5UxS5YsWeNxule99NUqbb/99ovvfOc72e3UGuyYY47JwrP0O5OkVnIDqZIBAIDBMtAeAABGuI022qjrdvqr/jW5+OKLs6DioosuyuaoDNSGG27YVVGQgoqBfGH+yCOP5FxnX2pqarIKhU9+8pNZC6hUjTJlypTsvhS8dB9a3l9AkFqJffWrX42bb745vvKVr3Tdl4ahd4Ytxx57bDz66KP9XtI+na+9s+ojVdYM5H1L+zU3N8dIsummm+b87PoLRDrfz9SmberUqTn3e+KJJ9Z4rMcee6zrdmdFyuo+8IEPZM+TpEqnJH3GnbQEAwBguAhXAABghEttqzrddttta9z/5z//eVx55ZVxxhln5PXlfxosv/3223dVb/z+979f42NuuOGGrts77rhj1+2rrroqPvrRj2ZD5/sLTLbYYos49NBDu37uDDVS0PLv//7v2SyVt7zlLX2+jtSmKj0+HafTnDlzIl9pqPx2223X9fNAXvsJJ5yQDVffa6+94le/+lUMlb5acRXijW98Y9ftG2+8cY37d99nm2226XN+zO23396jfVgu3UOSt7/97Tn32WCDDWK33XbLbqf2by+//HJWndQZqu29995rXDMAABSDcAUAAEa4N7/5zV1tlNIXzmmWSF/SfU8//XR2e/r06QOqJll9qHin8847r8d8lNWluRjdw5X3vOc9PWap3HnnnVkLqjVVo8yfP7/r9uTJk7sqXFJlRWoH9corr3RVMeSSvtTv3sas8xj5Si2pOl1wwQU91rW6VCFz6623Zs+dAqEUsgyVzkqOZE0BxkBeY2dYk6qGOttt5ZIql37wgx/k/HxXlwKtq6++us/70+9AZ3VLCsLS7+aafgdTwJcel1rHJbNmzYr6+vp+Xx8AABSLcAUAAEa49IXyUUcd1fXzF77whbjnnntytl1K1R6djj766IK+fO9sHZVag6XnzVUJkp4/zcNIs1I62zWldl+d3v/+93d9EZ5mq6TB8p37dpe+OE/twZL0pf873/nOrvsOPPDArtupzVkKc1aXvoBPA+/nzZuX/ZyqT/pqXbUmqUqms11Vqpj4+Mc/ng1VX919990Xxx13XNfP//qv/xpbbbVVDJUxY8Z03X7++ecHdazNNtssa72VtLS0xCc+8Yn4v//7v177vfjii9ncmXSdpEHzhxxySL/H/sY3vhE33XRTr+2rt277z//8z36P8653vatrFkwKd9I6Ey3BAAAYTgbaAwBAGTjiiCOySpBULZGqNFIrrFTRklpxpVkhDz/8cPYldmeAkb7w7/wSPR8pEPne974XH/nIR7KqlRQkpIqB1MZpyy23zI6ftqW1pGAjScHC1772tR7HWXfddbN5JmeddVb287nnnhu/+c1v4k1velPW+im1+XrooYeydlKdaz744INjxowZXcdIP6d2W2k2SnrNBx10UNYiLFU9pKHmKVBJj3/88cez/dO8mDV9cd+f1PIqvfb03qbKm/SepmqNt73tbbH11lvHqlWrskqP7pVDKchZ/bUX27Rp07pun3nmmVnolV5rCiEKCXXSetNrS2FcqgpKn/Uee+yR/S6l46b3M/0urVy5sivc+e53v9sVeOSSHpf2/8xnPpO19dp11127Qri77rqra7/03qZWcf1Jz5NCtvT70lk5ld6D7i3NAABgqAlXAACgDKSqjhRQfP3rX88ChxRspC/5c7UISxUfqdKjUClI+MUvfhGf//znsy/aV6xYEb/73e9y7psCnPRcTU1Nve5LVRGptdSFF16YtbNKVSC5KkFS26sPf/jD8aUvfalX0JMe+6lPfSr+8Y9/ZNv6es2pbVqqnNhll11iMLbddttsZk2qTEltrFLVxB/+8Ifssrqddtopzj777CzoGUop3EqffRoun0Km888/P9ue3vNCwpX0uFQtlKqcUru19Lv017/+NbusLlUCpdfY1wD6Tu9+97uz39EUiNx9993ZZfXPOL2nn/zkJwe0xtQaLB2r++9ZMWfPAADAmghXAACgTKSwIQUIqaIjDYxPFQFp3keq/Jg0aVIWLHzoQx8qyl/4pyqVa6+9NgtVUrCQZr10tt7acMMNs8qE1EYrBQxrGvr+3ve+NwuEUguw5557LpYvX55VQ6TZKKn6JrV7SsPSc1l//fXjl7/8ZTbbJQ1XT9UuqdoiveYUaqQ2V6mqJgVKY8eOjWJIlTFp1sf111+fDbZPwU567SkgSiHO9ttvH+973/tin3326TEPZaikz/bKK6/MQo5UCbJ48eIsIOlvHs6apPcqtdxKx/v1r3+dzZBJ83FSRVGqOkozZFJgkqpj0vybNUn7nH766dn+KbhJFT6p+if9rqTPOFWspN+pgdp9992z34/0+50UUoUFAACDUdXRWasPAAAARZLCvcMPP7yr0iSFK8WSArjUAi5dp3ZlqZIKAACGk4H2AAAAjCipWioFK53BDQAADDfhCgAAACNKaoPWOdw+tWADAIDhZuYKAAAAa600PyddGhsbs2qVc889N+67777svjSPJ83nAQCA4SZcAQAAYK21cuXKbID9OuusE4sXL46WlpZsewpVPvWpT5V6eQAAVCjhCgAAAGutFKKk9l/z5s3r2lZTUxOnnnpqTJ48uaRrAwCgcpm5AgAAwFptn332ibFjx0ZTU1PstttuceGFF8Z73vOeUi8LAIAKVtXR0dFR6kUAAAAAAACMFCpXAAAAAAAA8iBcAQAAAAAAyINwBQAAAAAAIA/CFQAAAAAAgDwIVwAAAAAAAPIgXAEAAAAAAMiDcAUAAAAAACAPwhUAAAAAAIA8CFcAAAAAAADyUJvPzqw95s5dUuolrDUmTBgdtbU10draFgsWLC/1coARxPkDKIRzB1Ao5w+gUM4fQKGcP143adLYKCaVK4x4VVVVPa4BBsr5AyiEcwdQKOcPoFDOH0ChnD+GjnAFAAAAAAAgD8IVAAAAAACAPAhXAAAAAAAA8iBcAQAAAAAAyINwBQAAAAAAIA/CFQAAAAAAgDwIVwAAAAAAAPIgXAEAAAAAAMiDcAUAAAAAACAPwhUAAAAAAIA8CFcAAAAAAADyIFwBAAAAAADIg3AFAAAAAAAgD8IVAAAAAACAPAhXAAAAAAAA8iBcAQAAAAAAyINwBQAAAAAAIA/CFQAAAAAAgDwIVwAAAAAAAPIgXAEAAAAAAMiDcIURrbmlLR54/JWYM29ZqZcCAAAAAECFqC31AqBQryxcEd+64t5YsGRV9vNR+86MN2+zfqmXBQAAAABAmVO5woh14/8+1xWsJJdf/3C0tLaVdE0AAAAAAJQ/4Qoj1tyFK3r8vLK5LV5ZtLJk6wEAAAAAoDIIVxix6mp7//qualG5AgAAAADA0BKuMGI11NX02raqWbgCAAAAAMDQEq5QVuFKc2t7SdYCAAAAAEDlEK4wYtXX5WgLpnIFAAAAAIAhVhsV4E9/+lNcffXVcf/998f8+fOjvr4+Ntlkk9hrr73i8MMPj4kTJxZ03Oeffz5+/OMfx+233x4vvfRSjBkzJmbMmBEHHXRQvO997yv662AAbcHMXAEAAAAAYIiVdbjS2toaJ598cvz2t7/tsb2lpSUeeuih7PLLX/4yzjvvvNhpp53yOvYDDzwQRxxxRCxbtqxr24IFC+LOO+/MLjfeeGN897vfjdrasn6L1762YMIVAAAAAACGWFm3BTvrrLO6gpV3vOMdceWVV2bBR9r2xS9+MUaPHh3z5s2LY445Jqs8Gag5c+bEJz7xiSxY2XTTTeNHP/pR/PWvf43/+Z//iQ9+8IPZPr///e+z52fo1OesXDFzBQAAAACAoVW24UoKSy699NLs9vvf//74wQ9+EDvvvHNMmDAhpk+fHkcffXR2f6osWbhwYRaQDNQFF1yQVamMGzcuLrvssnjb296WtRbbaqut4tRTT42Pf/zj2X7pvtQ6jOGbuaJyBQAAAACAoVa24cpNN92UtQVLjj/++Jz7bL/99rHPPvtkt2+99dYBHXfx4sXxq1/9Krt92GGHxfrrr99rn89+9rNZ8JLaj/36178exKugP2auAAAAAABQCmUbrrz88svR2NgY6623XkydOrXP/dJg+879B+Kuu+6KVatWdbUay6WpqSne9KY3dYU8DOfMFW3BAAAAAAAYWmUbrqRqlb/97W/ZYPn+PPPMM9n1OuusM6DjPvzww9l1aie29dZb97nfNttsk10/9thj0dzcnMfKGdzMFZUrAAAAAAAMrbINVzqNGTOm37kst9xyS3b7jW9844CO98ILL2TXU6ZMiZqa3l/ud9pwww2z67a2tpgzZ06eq2YgtAUDAAAAAKAUyj5c6UtHR0d89atf7WrxdcghhwzocWmQ/UAqXcaOHdt1e9GiRYNaK7k15BhoL1wBAAAAAGCo1UaF+ta3vtU1xP5973tf7LHHHgN6XGcY09DQ0O9+ad7L6o8ppgkTRkdVVVVUspbo/fo7ImLixKaSrAcYeaqrq7qunTuAgXLuAArl/AEUyvkDKJTzx9CprcSKldNPPz0uueSS7Ofp06fH17/+9QE/vr9WYMOptnbtWEcpjW6sy1m5UlNTsQVZQIFSWF1TU9mBNZA/5w6gUM4fQKGcP4BCOX8UX0WFK2mw/Je+9KW49tprs5+32GKL+MlPfhJNTQNP7EaNGjWgapSVK1fmrGIpltbWtoqvXKmr7f36V65qi7a29pKsBxh50l9tpHNpCt7b21PtG8CaOXcAhXL+AArl/AEUyvnjdcX+o/yKCVcWLlwYn/3sZ+N///d/s5+32267uPDCC2PixIl5HWfcuHHZ9dKlS/vdb/HixV23J0yYEMW2YMHyqHTtHb1PBstXtsT8+ctKsh5g5EnlsOmvNtJ/XDh3AAPl3AEUyvkDKJTzB1Ao54/XTZr0+pz0YqiI/knPPvtsfOhDH+oKVt761rfGZZddlnewkmy66abZ9YsvvpilfX1J9ye1tbUxadKkgtdO36qrqqJ+taH2zQbaAwAAAAAwxMo+XPnnP/+ZBStPP/109vMHP/jB+OEPf5hXK7Du0oyWzhZjjz/+eJ/7PfTQQ9n1lltuGfX19QU9F2tWv9rsmVUtWoIBAAAAADC0yjpcee655+JjH/tYzJ8/P/v585//fJx66qlZNUmhdtttt665KzfffHPOfZYvXx533nlnV5UMQ6ehrqZX5Up/FUUAAAAAADBYZRuutLS0xHHHHRdz587Nfv6P//iP+PSnPz3o46aKl3e+853Z7Z/85Ccxe/bsXvuce+652cyVurq6OPTQQwf9nPStob5nuJJilZZW1SsAAAAAAAydsh1o/4tf/CL+8Y9/ZLff/e53x0EHHRTLlvU/sKd7q7BZs2Zl1zvssEOcccYZPfb7whe+EDfddFMsXLgwPvKRj8TJJ58cu+66ayxYsCAuueSS7LmTww47LKZMmTIEr45O9bW988FVLW1Rv1pFCwAAAAAAFEvZhisp5Oh0/fXXZ5c1efTRR7tuP/XUU9l1rmH0G2ywQZxzzjlx7LHHZpUrn/vc53rtk8KZE088cRCvgELagnWGK2NLshoAAAAAACpBWYYracbKs88+O6TPkWapXHfddXHBBRfE7bffHi+99FI2uH7rrbeOAw88MA444ICoqqoa0jXQuy1YYqg9AAAAAABDqSzDlYkTJ/aoQinEQB4/derUOOWUUwb1PAxOrvZfaag9AAAAAAAMlbIdaE9laMgxc0W4AgAAAADAUBKuMKLV52wLJlwBAAAAAGDoCFcou4H2zWauAAAAAAAwhIQrlF24onIFAAAAAIChJFxhRKuv6/0rLFwBAAAAAGAoCVcY0VSuAAAAAAAw3IQrjGhmrgAAAAAAMNyEK4xoKlcAAAAAABhuwhVGNDNXAAAAAAAYbsIVyq8tWLNwBQAAAACAoSNcYUSrz9UWrNXMFQAAAAAAho5whTIcaK9yBQAAAACAoSNcofxmrmgLBgAAAADAEBKuUH6VK63CFQAAAAAAho5whbILV1a1mLkCAAAAAMDQEa4wotXVVkdVVc9t2oIBAAAAADCUhCuMaFVVVb2qV1YZaA8AAAAAwBASrjDiNdT3DFfMXAEAAAAAYCgJVxjxGutre/zc3NIe7R0dJVsPAAAAAADlTbhCWQ61bzHUHgAAAACAISJcoezagiWrtAYDAAAAAGCICFcY8RpzhCvNzcIVAAAAAACGhnCFEa9htZkryaoW4QoAAAAAAENDuEJZzlxZZeYKAAAAAABDRLhCebYFU7kCAAAAAMAQEa5QngPthSsAAAAAAAwR4QojXqOZKwAAAAAADCPhCmU6c0W4AgAAAADA0BCuUJZtwZoNtAcAAAAAYIgIVxjxDLQHAAAAAGA4CVcY8Qy0BwAAAABgOAlXGPG0BQMAAAAAYDgJVxjxGutre21TuQIAAAAAwFARrjDiaQsGAAAAAMBwEq4w4jXUCVcAAAAAABg+whVGvEYzVwAAAAAAGEbCFUa8BjNXAAAAAAAYRsIVyrJyRbgCAAAAAMBQEa5QljNXmoUrAAAAAAAMEeEKI15dbXVUV1f12KZyBQAAAACAoSJcYcSrqqqKUau1BlvVLFwBAAAAAGBoCFcoC40NPYfarxSuAAAAAAAwRIQrlIXG+p7hSlt7R7S2tZdsPQAAAAAAlC/hCmVhVEPvofaqVwAAAAAAGArCFcqyLVhi7goAAAAAAEOh4sKVb3zjGzFjxoy45pprBn2sv//973HCCSfEXnvtFTNnzoxddtklDj744Lj00kujubm5KOulsLZgycoW4QoAAAAAAMXX+xvpMnbTTTfFFVdcUZRjpQDl9NNPj7a217/Ab2lpifvuuy+7/PrXv44LL7wwJk6cWJTno3+jVK4AAAAAADBMKqZy5eabb47jjjsu2tsHP+T8jjvuiNNOOy0LVjbffPP4wQ9+ELfddltce+21cdhhh0V1dXU8+OCDcfzxxxdl7axZY33vmSurmltLshYAAAAAAMpb2VeupDDl+9//fpx//vlFCVaSCy64IDo6OmLSpElZJUxndcr6668fX/7yl6OpqSl++MMfxp133hn33ntv7LzzzkV5XvKrXNEWDAAAAACAoVDWlSupmmTfffeN8847LwtWtttuu6Ic94EHHsiu99lnn5xtvz784Q/32pehZaA9AAAAAADDpawrV4466qjsuq6uLo455pj4wAc+EO985zsHfdzU9itpbc3ddqq2trbXvgx/WzCVKwAAAAAADIWy/ua/qqoq3vWud8VvfvOb+OxnP1u0oGOHHXbIrm+55ZZYsGBBr/uvvvrqrttagg0PA+0BAAAAABguZV25cv3118dmm21W9ON+7nOfi3vuuSdeeeWVOPzww+OEE06IbbfdNhYvXpwNtb/ooouy/Q488MCYOXNm0Z+f3hrrc4QrKlcAAAAAABgCZR2uDEWwkuy4445x8cUXxze/+c148MEH45Of/GSP+8ePHx+f+tSnsuBlqEyYMDqrzCG1XqvKWblSVVMdEyc2lWRNwMg5f3ReO18AA+XcARTK+QMolPMHUCjnj6FT1uHKUFq6dGk0NeX+ZVyyZEk2yP6FF16IjTbaaEiev7a294yRStbYUJOzLVhNTVl3vgOKJIXVNTUCayA/zh1AoZw/gEI5fwCFcv4oPuFKAX7yk5/Et7/97ez2rFmzssqVLbfcMgtc/vznP8dZZ50V1113Xdx9991x6aWXxuabb170NbS2tqlceU1KXXO1BVuxqjXa2tpLsiZg5Jw/0rm0o6Mj2ts7Sr0cYIRw7gAK5fwBFMr5AyiU88friv2H+MKVPD355JNx5plnZrcPPvjgOOWUU7rumzhxYuy3336x++67x0EHHRRz587N7r/kkkuKvo4FC5YX/ZgjVSpny9UWbPGSVTF//rKSrAkYOeeP9Fcb6T8unC+AgXLuAArl/AEUyvkDKJTzx+smTRobxaRnUp6uvvrqaGtri8bGxjjxxBNz7rPBBhvEMccck92+88474+mnnx7mVVaeXG3BVhpoDwAAAADAEBCu5KkzKNlqq61izJgxfe6322679ah2YWiNytEWLM1cAQAAAACAYhOu5KmlpSW7bm5uHvBj8tmXwjTmaAu2UrgCAAAAAMAQEK7kabPNNsuun3jiiXj55Zf73O+ee+7pur3FFlsMy9oqWUNd77Zgq1paS7IWAAAAAADKm3AlT+9973uz69bW1jjttNOivb291z4pdDn//POz2zNmzMhaiDG0qqurorG+Z8CiLRgAAAAAAENBuNKHWbNmZZeTTjqpx/YddtghDjjggOz29ddfH0cccUTcdtttMW/evJgzZ05cc8018cEPfjALWOrq6uKrX/1qiV5B5Wlcbe6KgfYAAAAAAAyF3oMqyDz11FPZ9aRJk3rdd8opp2SzV37729/GXXfdlV1W19TUFGeccUbssssuw7Je0tyVmoilr//c3NIe7e0dWVULAAAAAAAUi3ClAPX19XHmmWfG/vvvH1dddVXcd999WeVKqlTZaKONYs8994zDDjssJk+eXOqlVnTlSrKqpS1G5Rh2DwAAAAAAhaqob52nTZsWjz766ID2Hch+b3nLW7ILa4dRqXJlNcIVAAAAAACKzcwVykZDrsoVQ+0BAAAAACgy4Qplo7G+d+XKSuEKAAAAAABFJlyhbORq/5XaggEAAAAAQDEJVyjrgfYqVwAAAAAAKDbhCmWjsY+B9gAAAAAAUEzCFcq8cqW1JGsBAAAAAKB8CVcoG6NyDLRfpS0YAAAAAABFJlyhbDQaaA8AAAAAwDAQrlA2DLQHAAAAAGA4CFco74H2whUAAAAAAIpMuELZGJWrckVbMAAAAAAAiky4QnnPXFG5AgAAAABAkQlXKBuN9TnagqlcAQAAAACgyIQrlHXlioH2AAAAAAAUm3CFsjEqV+WKcAUAAAAAgCITrlA2Ggy0BwAAAABgGAhXKBt1tdVRW1PVY9uq5taSrQcAAAAAgPIkXKGsNNT1bA1moD0AAAAAAMUmXKGsNK42dyUNtO/o6CjZegAAAAAAKD/CFcp67krKVVpa20u2HgAAAAAAyo9whbJuC5YYag8AAAAAQDEJVyjrtmDJqmbhCgAAAAAAxSNcoewrV4QrAAAAAAAUk3CFsq9c0RYMAAAAAIBiEq5QVhq0BQMAAAAAYIgJVyj/gfbCFQAAAAAAiki4QvkPtG9pLclaAAAAAAAoT8IVyoq2YAAAAAAADDXhCmWlMVdbMAPtAQAAAAAoIuEKZUXlCgAAAAAAQ024QllpqKvttc1AewAAAAAAikm4QtkPtBeuAAAAAABQTMIVykpjQ65wpbUkawEAAAAAoDwJVygrjfXaggEAAAAAMLSEK5SVUTnagq1YpXIFAAAAAIDiEa5QVlSuAAAAAAAw1IQrlP1Ae5UrAAAAAAAUk3CFslJdXRUNdT0DFpUrAAAAAAAUk3CFstPYsHq4onIFAAAAAIDiEa5QdkatNnelta0jWlrbS7YeAAAAAADKi3CFipi7onoFAAAAAIBiEa5QdkY19KxcScxdAQAAAACgWIQrVETlyopVKlcAAAAAACgO4Qplp3G1mSuJyhUAAAAAAIql4sKVb3zjGzFjxoy45pprBn2s5ubmuPTSS+Pggw+O3XffPWbOnBl77713fPnLX46nn366KOslf40NZq4AAAAAADB0ev+Jfxm76aab4oorrijKsWbPnh1HHnlkPPnkkz22v/DCC3HVVVfFb3/72/jud7+bhS0Mr1E5KldWrFK5AgAAAABAcVRM5crNN98cxx13XLS3tw/6WCtWrIgjjjgiC1bq6uri85//fPzhD3/InuO0006L8ePHx8qVK+OEE07IQhhKP3NF5QoAAAAAAMVS9uFKClPOOeec+MxnPhMtLS1FOeb5558fzzzzTFRXV8d5550Xn/70p2PjjTeOqVOnxoEHHhiXXHJJ1NbWxvLly+Oyyy4rynMycKMaVK4AAAAAADB0yjpcue2222LffffNApAUsmy33XZFmbPy85//PLt90EEHxV577dVrn6233jr22GOPqKmpiUceeWTQz0l+VK4AAAAAADCUynrmylFHHZVdp9ZdxxxzTHzgAx+Id77znYM65h133BGLFi3Kbh999NH9Vrek562qqhrU85G/xhwzV1Y2q1wBAAAAAKA4yjpcScFGClPSrJUtttginn/++UEf84EHHsiuUwuwjTbaqMd9qe1YClSS+vr6QT8XhRnV0LtyZcUqlSsAAAAAABRHWYcr119/fWy22WZFPeY///nP7HrTTTfNru+55564+OKL46677oolS5Zkw+z33HPPbA5LsZ+bgVG5AgAAAADAUCrrmStDEW7MnTs3u04hSmr9deihh8ZNN92UBSvJwoUL49prr4399tsv285aUrli5goAAAAAAEVS1pUrQ2HZsmXZ9d133x3XXXddTJ8+Pb74xS/GbrvtlrUFu+WWW+KMM86IV155JU444YT45S9/GTNmzCj6OiZMGG2ey2uqq6u6ridObIqOmt6ZYVt7R3YfQH/nD4CBcO4ACuX8ARTK+QMolPPH0BGu5GnFihVdFSxpjsuVV14ZY8aMybaNGjUq9t1339h+++3jwAMPjOXLl8fZZ5+dVbgUW21t7+qMSpfCppqaqhgzuve8mxWr2qImR+gC0P38AZAP5w6gUM4fQKGcP4BCOX8Un3AlTylA6XT88cd3BSvdbb755lm4ctlll8Vtt92WhSyjR48u6jpaW9tUrrwmpa7pvejo6Ij29o6oyxGiLF/ZEm1t7SVZHzByzh8AA+HcARTK+QMolPMHUCjnj9cV+4/vhSt5amp6vXRq991373O/XXfdNQtXUquwZ599NrbeeuuirmPBguVFPd5IlsrZUuqaTg7z57/atq2xvqbHEPtlK1q67gPo7/wBsCbOHUChnD+AQjl/AIVy/njdpEljo5j0ScrT1KlTu243NDT0uV/3ipZVq1YN+broKYUr3aWgJaWzAAAAAAAwWMKVPG2zzTZdt5977rk+90sD7TtNnjx5yNdFT6MaansNtG/VFgwAAAAAgCIQruTpbW97W9ftG264oc/9/vKXv2TXG2ywgXClBBrra3MOtQcAAAAAgMESruRpyy23jJ133jm7fdFFF8WTTz7Za5/7778/fve732W399tvP4Pn14K2YMnK5taSrAUAAAAAgPIiXOnDrFmzsstJJ53U675TTjklm7eyfPny+PCHPxxXXHFFzJ49O1566aX42c9+FkceeWQ2yH7atGlx9NFHl2T9lW71tmCJyhUAAAAAAIqh9zfQZJ566qnsetKkSb3umz59elxwwQXxuc99LhYuXBhf//rXs0t3KVj54Q9/GE1NTcO2Zl6ncgUAAAAAgKEiXCnQHnvskc1cueSSS+Lmm2+O559/Pqqrq2OjjTaKd7/73VlFy7hx40q9zIo1KtfMlWaVKwAAAAAADF5FhSupmuTRRx8d0L4D2W/ixIlx/PHHZxfWLo0NKlcAAAAAABgaZq5QOW3BzFwBAAAAAKAIhCuUpcYcbcFWagsGAAAAAEARCFcoS6NytAVbsUpbMAAAAAAABk+4QsVUrqwwcwUAAAAAgCIQrlCWRuWauaItGAAAAAAARSBcoSw1NuSYuaItGAAAAAAARSBcoSw1qlwBAAAAAGCICFcoS6NyVK6YuQIAAAAAQDEIVyhLKlcAAAAAABgqwhXKUkNdTVStts3MFQAAAAAAikG4QlmqqqqKxoae1SsqVwAAAAAAKAbhCmWrsb7n3JUVq9qio6OjZOsBAAAAAKA8CFeomLkr7R0d0dzaXrL1AAAAAABQHoQrlK1RDT0rVxKtwQAAAAAAGCzhCmVr1GqVK4mh9gAAAAAADJZwhYqZuZKoXAEAAAAAYLCEK5StxobelSsrVK4AAAAAADBIwhUqqnJlRbNwBQAAAACAwRGuULZG5xhor3IFAAAAAIDBEq5QtkblCFeWrxSuAAAAAAAwOMIVytboRpUrAAAAAAAUn3CFimoLtly4AgAAAADAIAlXqKi2YCpXAAAAAAAYLOEKFdUWbPmqtpKsBQAAAACA8iFcobIqV1a2lGQtAAAAAACUD+EKFTZzReUKAAAAAACDI1yhoipXDLQHAAAAAGCwhCuUrbra6qit6fkrbqA9AAAAAACDJVyhoobaL18pXAEAAAAAYHCEK1RUa7DWtvZoaW0v2XoAAAAAABj5hCtU3FB7rcEAAAAAABgM4QplbXRDTa9thtoDAAAAADAYwhXK2qjGul7bVK4AAAAAADAYwhUqr3LFUHsAAAAAAAZBuEJZG92gcgUAAAAAgOISrlDWRpm5AgAAAABAkQlXKGujGmp7bdMWDAAAAACAwRCuUNZGN+YIV1SuAAAAAAAwCMIVKq5yxcwVAAAAAAAGQ7hCWRstXAEAAAAAoMiEK5Q1M1cAAAAAACg24QoVN3NF5QoAAAAAAIMhXKHi2oIZaA8AAAAAwGAIVyhrjQ21UbXaNpUrAAAAAAAMhnCFslZdVRWNDTU9tpm5AgAAAADAYFRcuPKNb3wjZsyYEddcc03Rj93e3h4f+chHsuOffPLJRT8+xRlqv6K5NTo6Okq2HgAAAAAARraKClduuummuOKKK4bs+BdeeGHcc889Q3Z8ijN3JeUqK5vbSrYeAAAAAABGtooJV26++eY47rjjsuqSofDQQw/FOeecMyTHpriVK4m5KwAAAAAAFKr3t85lJoUp3//+9+P8888fsmBl1apVceKJJ0ZLS8uQHJ/iVq4ky1e1xsSSrAYAAAAAgJGurCtXbrvttth3333jvPPOy4KV7bbbbkie5//9v/8Xjz/+eOyxxx6x4YYbDslzULhRjTnCFUPtAQAAAAAoUFmHK0cddVQ89thjUVdXF8cee2ycffbZRX+OO+64Iy6//PIYO3ZsfOtb34qqqqqiPwfFr1zRFgwAAAAAgEKVdVuwFHS8853vzGatbLHFFvH8888X9fiLFi2Kk08+OTo6OuJLX/qSqpURNHMltQUDAAAAAIBClHW4cv3118dmm202ZMf/2te+Fi+99FLss88+sf/++w/Z8zA4KlcAAAAAACimsg5XhjJY+c1vfpOFN+uuu26ceuqpMdwmTBitBdlrqquruq4nTmzqdf96ObZFdXXOfYHKsqbzB0Auzh1AoZw/gEI5fwCFcv4YOmUdrgyV2bNndwUqX//612PixInDvoba2pphf861XQqbamp6B05jR9fnrFypqSnrkUNAEc4fAP1x7gAK5fwBFMr5AyiU80fxCVfy1N7eHv/+7/8eS5YsiQMOOCBrCVYKra1tKldek1LX9F6k2Tft7R297h/V0DuIWrq8Jdra2odphcBIPX8A5OLcARTK+QMolPMHUCjnj9cV+4/thSt5uvjii+Puu++OqVOnZkPsS2XBguUle+61TSpnS6lrOjnMn7+s1/2tzb3nqyxYvCLnvkBlWdP5AyAX5w6gUM4fQKGcP4BCOX+8btKksVFM+iLl4ZFHHomzzz47S/pOO+20GDNmTKmXxACMbuydIS430B4AAAAAgAKpXMnDH/7wh2hubs5uf/SjH+133//+7//OLsmll14au++++7Cskd5GNfT+NV+xUrgCAAAAAEBhVK5Q9kbnCFdUrgAAAAAAUCiVK3n45Cc/GR//+Mf73ed973tfzJ49O97//vfHKaeckm1rbGwcphWSS11tddRUV0Vbt4FNK4QrAAAAAAAUSLiSh/r6+uzSnzSPJamtrY2mpqZhWhlr+kxSa7ClK1q6tqlcAQAAAACgUMKVPsyaNSu73mGHHeKMM84o9XIowlD77uFKc0t7tLa1R22NzngAAAAAAORHuNKHp556KrueNGlSqZdCETQ15pi7srI1xjX1X4kEAAAAAACr82f7VISmxrpe25atfL2SBQAAAAAABqqiKlemTZsWjz766ID2Heh+q7v55psLehxDq2lUjnBlhbkrAAAAAADkT+UKFTNzZXUqVwAAAAAAKIRwhYqgLRgAAAAAAMUiXKEijMlVuaItGAAAAAAABRCuUBFGq1wBAAAAAKBIhCtUhKZRuWauqFwBAAAAACB/whUqdubKcpUrAAAAAAAUQLhCRWjKNXNF5QoAAAAAAAUQrlARmkblmLmyQuUKAAAAAAD5E65QEVSuAAAAAABQLMIVKkJdbU3U1/b8dV9m5goAAAAAAAUQrlCxrcGWrWiNjo6Okq0HAAAAAICRSbhCxRi9Wmuw9o6OWNncVrL1AAAAAAAwMglXqBhNjTmG2msNBgAAAABAnoQrVPZQ+xWG2gMAAAAAkB/hChVdubJc5QoAAAAAAHkSrlAxmkblqFxZqXIFAAAAAID8CFeoGGauAAAAAABQDMIVKnvmisoVAAAAAADyJFyhYjSNylG5skLlCgAAAAAA+RGuUOFtwVSuAAAAAACQH+EKFWN0zrZgKlcAAAAAAMiPcIWKoS0YAAAAAADFIFyhYozJUbmyXFswAAAAAADyJFyhYjQ21EbVatu0BQMAAAAAIF/CFSpGdVVVr7krS1WuAAAAAACQJ+EKFaWpsefclVXNbdHa1l6y9QAAAAAAMPIIV6goTaPMXQEAAAAAYHCEK1R05Upi7goAAAAAAPkQrlBRVp+5kixTuQIAAAAAQB6EK1SUplE5KldWqFwBAAAAAGDghCtEpbcFM3MFAAAAAIB8CFeoKE052oItNXMFAAAAAIA8CFeoKDkH2msLBgAAAABAHoQrVJSmUb0rV7QFAwAAAAAgH8IVKkrOyhVtwQAAAAAAyINwhaj0mSvLVK4AAAAAAJAH4QoVZcyo3pUrS81cAQAAAAAgD8IVKkpTrnBluXAFAAAAAICBE65QUWprqmNUQ8/WYEtUrgAAAAAAkAfhChVn7GrVKytWtUZrW3vJ1gMAAAAAwMgiXKHijBnduzXYMtUrAAAAAAAMkHCFipNrqL3WYAAAAAAADJRwhaj0tmCJofYAAAAAAAyUcIWKk6st2FKVKwAAAAAADFDFhSvf+MY3YsaMGXHNNdcM+lj33XdfnHjiibH33nvH9ttvHzvttFO8973vjdNOOy1eeOGFoqyX4tMWDAAAAACAwaiNCnLTTTfFFVdcUZRj/b//9//iwgsv7LGtubk5Hn/88exy1VVXZfvss88+RXk+imfs6Ppe25Ysby7JWgAAAAAAGHkqpnLl5ptvjuOOOy7a29sHfazLL7+8K1jZZZdd4ic/+Un89a9/jeuvvz5OOeWUGD9+fCxfvjyOP/74ePjhh4uweoa6csXMFQAAAAAABqrsw5UUppxzzjnxmc98JlpaBv8FeqpOScdLdtttt7jkkkviLW95S0ycODE233zzOPjgg+Pqq6+OcePGZfueffbZRXgVDHm4oi0YAAAAAAADVNbhym233Rb77rtvnHfeeVnIst122w36mKlCZdGiRdntY489Nmpre3dWmzZtWhx00EHZ7b/85S9FCXUonrE5BtqbuQIAAAAAwECVdbhy1FFHxWOPPRZ1dXVZEFKMKpIXX3wxRo8end1+wxve0Od+m2yySXadgpUFCxYM+nkZ2pkr2oIBAAAAADBQZT3QvqqqKt75zndms1a22GKLeP755wd9zNT2K12WLl0aDQ0Nfe73zDPPdN1OLcJYe4xuqI2qqoiOjte3LV1hoD0AAAAAAANT1uFKGjC/2WabDcmxx4wZ0+d9K1asiGuvvTa7nVqRNTY2DskaKEx1dVU0Ndb1mLOiLRgAAAAAAANV1m3BhipYWZNvf/vbMXfu3Oz2Rz7ykZKsgfzmrjS3tMeqlraSrQcAAAAAgJGjrCtXSuGnP/1pXHnlldntXXbZJfbff/8heZ4JE0Znbc94tRKl83rixKYBPWb82MZ4cd7yHttqG+pi4vhRQ7JGoHzOHwDOHUChnD+AQjl/AIVy/hg6wpUiByvf+ta3stuTJ0+O73znO1FdPTTFQbW1NUNy3JEshU01NQMLnNYZ03uo/bIVLTFlXScYqET5nD8AOjl3AIVy/gAK5fwBFMr5o/iEK0XQ0dERZ511Vvz4xz/Ofp40aVJcfPHFWcAyVFpb21SuvCalrum9SJ9De3u3KfX9GDu6d7iycMmqaGtrH4IVAuV0/gBw7gAK5fwBFMr5AyiU88framqKWwghXBmklStXxkknnRQ33nhj9vO0adPiJz/5SWyyySZD+rwLFvRsaVXJUjlbSl3TyWH+/GUDekzda+Vw3c1+eXFsvN7oIVghUE7nDwDnDqBQzh9AoZw/gEI5f7xu0qSxUUzClUGYP39+fOpTn4r7778/+3m77baLCy64INZbb71SL401GDOq50D7ZOnylpKsBQAAAACAkWVoBoJUgJdeeikOPvjgrmDl7W9/e1x++eWClRFi7Ogc4coK4QoAAAAAAGsmXCnAggUL4ogjjohnnnkm+/lDH/pQnHfeeTF6tJZSI7lyZYnKFQAAAAAABkBbsAJ86UtfiieffDK7ffjhh2c/M7KMyVG5skTlCgAAAAAAAyBc6cOsWbOy6x122CHOOOOMru233HJL/PGPf8xu77TTTvG5z30uli3rfxBQqmipquo9QJ3SGZtz5kpzSdYCAAAAAMDIIlzpw1NPPZVdT5o0qcf2Sy65pOv2fffdF7vssssaj5XCmGnTpg3BKinU2NH1vbaZuQIAAAAAwECYuZKnv/3tb6VeAkXQWF8TNdU9q4m0BQMAAAAAYCAqqnIlVY88+uijA9q3r/1StQojX2rTluauLFr6eiuwpctboqOjQws3AAAAAAD6pXKFirX63JW29o5Y2dxWsvUAAAAAADAyCFeoWGNyDLXXGgwAAAAAgDURrlCxxuQaar9cuAIAAAAAQP+EK1Ss1duCJUtXvD6DBQAAAAAAchGuULFytgVTuQIAAAAAwBoIV6hYY0YLVwAAAAAAyJ9whYo1LsfMlcXLtQUDAAAAAKB/whUq1rimHOHKMuEKAAAAAAD9E65QsYQrAAAAAAAUQrhCxRqXY+aKcAUAAAAAgDURrlCxmkbVRXVVVY9ti8xcAQAAAABgDYQrVKwUrIxt6lm9smRZS7R3dJRsTQAAAAAArP2EK1S0dUb3nLuSgpXlK1tLth4AAAAAANZ+whUqWq6h9ovMXQEAAAAAoB/CFSparnDFUHsAAAAAAPojXKGiCVcAAAAAAMiXcIWKNm61mSuJcAUAAAAAgP4IV6ho6+SqXFkuXAEAAAAAoG/CFSqagfYAAAAAAORLuEJFGzu6rtc2bcEAAAAAAOiPcIWKlrMtmHAFAAAAAIB+CFeoaGNG10XVatvMXAEAAAAAoD/CFSpaTXV1FrCsXrnS0dFRsjUBAAAAALB2E65Q8VYfat/a1hErVrWVbD0AAAAAAKzdhCtUvHGjc8xd0RoMAAAAAIA+CFeoeIbaAwAAAACQD+EKFW/1tmCJcAUAAAAAgL4IV6h4ucKVRcIVAAAAAAD6IFyh4uWcuSJcAQAAAACgD8IVKt64prpe2wy0BwAAAACgL8IVKp6ZKwAAAAAA5EO4QsXTFgwAAAAAgHwIV6h4BtoDAAAAAJAP4QoVr7amOpoaa3tsM3MFAAAAAIC+CFcgR/VKc0t7rGpuK9l6AAAAAABYewlXoI+5K4uWrSrJWgAAAAAAWLsJVyAi1hnTO1xZuFRrMAAAAAAAehOuQESMH9PQa9vCpSpXAAAAAADoTbgCfYUrS4QrAAAAAAD0JlyBFK6M1RYMAAAAAICBEa5AREzQFgwAAAAAgAESrkBWudI7XFmgLRgAAAAAADkIV8BAewAAAAAA8iBcgYhoqKuJ0Q21PbYtWLoqOjo6SrYmAAAAAADWTsIV6KM1WHNLe6xY1Vay9QAAAAAAsHaquHDlG9/4RsyYMSOuueaaQR/r+eefj6997Wvxjne8I2bOnBl77LFHfPSjH43/+Z//KcpaGV4TxtT32qY1GAAAAAAAq+vZB6nM3XTTTXHFFVcU5VgPPPBAHHHEEbFs2bKubQsWLIg777wzu9x4443x3e9+N2prK+otLru5K6k12IbrNZVkPQAAAAAArJ0qpnLl5ptvjuOOOy7a29sHfaw5c+bEJz7xiSxY2XTTTeNHP/pR/PWvf80qVj74wQ9m+/z+97+Ps846qwgrp1RtwZKFS1SuAAAAAABQYeFKClPOOeec+MxnPhMtLS1FOeYFF1yQVamMGzcuLrvssnjb294WEydOjK222ipOPfXU+PjHP57tl+5LrcMYuZUr2oIBAAAAAFBR4cptt90W++67b5x33nlZyLLddtsN+piLFy+OX/3qV9ntww47LNZff/1e+3z2s5/NgpcU5vz6178e9HNSwnBlSXNJ1gIAAAAAwNqrrMOVo446Kh577LGoq6uLY489Ns4+++xBH/Ouu+6KVaterWZIg+xzaWpqije96U1dc14YGSbkagumcgUAAAAAgEoKV6qqquJd73pX/OY3v8mqSaqrB/9yH3744ew6Darfeuut+9xvm222ya5TuNPcrPphJBg/pj7nQHsAAAAAAOiuNsrY9ddfH5tttllRj/nCCy9k11OmTImampo+99twww2z67a2tpgzZ05svPHGRV0HxTeuqT6qIqKj2zaVKwAAAAAAVFS4UuxgJUmD7JN11lmn3/3Gjh3bdXvRokVFX8eECaOzyhwiqquruq4nTmwa1LHGj22IBUteD1QWLW2O8eNHdz0HUF6Kef4AKodzB1Ao5w+gUM4fQKGcP4ZOWYcrQ6Fz3kpDQ+/5HN01Njb2ekwx1db2XTVTqVLYVFMzuBBk4jqNPcKVtvaOWLqyJSaMff3zBMpPMc4fQOVx7gAK5fwBFMr5AyiU80fxCVfy1F8rsOHU2tqmcuU1KXVN70VHR0e0t3dv6pW/iWMb44noWWn0yoIVMW5073kswMhXzPMHUDmcO4BCOX8AhXL+AArl/PG6mprijqAXruRp1KhRA6pGWblyZc4qlmJZsGB50Y85UqVytpS6ppPD/PnLBnWspobe4dnTLyyM8aP8U4FyVMzzB1A5nDuAQjl/AIVy/gAK5fzxukmTXh/lUQzFjWoqwLhx47LrpUuX9rvf4sWLu25PmDBhyNdFcYwf07vdm6H2AAAAAAB0J1zJ06abbppdv/jii1kpVV/S/UltbW1MmjRp2NZHDHqg/eoWdpvBAgAAAAAAwpU8TZ8+Pbtubm6Oxx9/vM/9Hnrooex6yy23jPp68zpGCpUrAAAAAACsiXAlT7vttlvX3JWbb7455z7Lly+PO++8M7v91re+dVjXx+BMyFW5srS5JGsBAAAAAGDtJFzJU1NTU7zzne/Mbv/kJz+J2bNn99rn3HPPzWau1NXVxaGHHlqCVVKo8WN6Vxkt0BYMAAAAAIBuhCt9mDVrVnY56aSTet33hS98IUaPHh0LFy6Mj3zkI3HjjTfG/Pnz44knnoivfvWrWeiSHHbYYTFlypQSrJ5CjRlVF7U1Pf9ZCFcAAAAAAOiutsdPdHnqqaey61zD6DfYYIM455xz4thjj80qVz73uc/12icFMyeeeOKwrJXiqaqqionjGuLlBSu6ti1d0RKrmtuiob6mpGsDAAAAAGDtoHKlQGmWynXXXRcHH3xwTJs2LWsBllqGvfGNb4zTTjstzj777Kiu9vaOROuOa+y17ZXFK0uyFgAAAAAA1j4VVbmSQpBHH310QPsOZL+pU6fGKaecUoSVsbaHK/MWrYyp6zWVZD0AAAAAAKxdlFbAatZdJ0e4onIFAAAAAIDXCFdggJUrAAAAAACQCFdgAJUr81WuAAAAAADwGuEKDCBcMdAeAAAAAIBOwhVYzcSxDVG12jZtwQAAAAAA6CRcgdXU1lTHOmPqe2xbuHRVtLa1l2xNAAAAAACsPYQrMIDWYB0dEQuWrCrZegAAAAAAWHsIVyCHdcf1nruiNRgAAAAAAIlwBQY41H6eofYAAAAAAAhXILf1clWuCFcAAAAAABCuQG4TtQUDAAAAAKAPwhXIQVswAAAAAAD6IlyBHAy0BwAAAACgL8IVyGFUQ200Ndb22DZv8apo7+go2ZoAAAAAAFg7CFdggNUrrW3tsWRZc8nWAwAAAADA2kG4AnnMXXnF3BUAAAAAgIonXIE+TMwxd2X+4lUlWQsAAAAAAGsP4Qr0wVB7AAAAAAByEa5AH9bL1RZs0YqSrAUAAAAAgLWHcAXymLkyd6HKFQAAAACASidcgT6sP2FUr20vL1S5AgAAAABQ6YQr0Iemxrpoaqztse2VhSuivb2jZGsCAAAAAKD0hCuQR/VKW3tHzF+iNRgAAAAAQCUTrkA/Jo3v3Rps7gKtwQAAAAAAKplwBfph7goAAAAAAKsTrkCelSvCFQAAAACAyiZcgX5MnjC61zZtwQAAAAAAKptwBfqhcgUAAAAAgNUJV6Af48fUR31tz38mLy9YER0dHSVbEwAAAAAApSVcgX5UVVXFpNWG2q9sbovFy1tKtiYAAAAAAEpLuAJrMGVi77krc+YtK8laAAAAAAAoPeEKFBCuvGSoPQAAAABAxRKuwBpMnpCjcmX+8pKsBQAAAACA0hOuwBpMWTdXWzDhCgAAAABApRKuQEFtwYQrAAAAAACVSrgCazBmVF00Ndb22PbyghXR1t5esjUBAAAAAFA6whUooDVYW3tHvLJoZcnWAwAAAABA6QhXYACm5Bpqb+4KAAAAAEBFEq5AgUPtXxSuAAAAAABUJOEKDMCG6zb12jb7lWUlWQsAAAAAAKUlXIEB2HC93uHKC8IVAAAAAICKJFyBAVhvfGPU1vT85zJ73rLo6Ogo2ZoAAAAAACgN4QoMQE11dUyZ2HPuyqrmtliwZFXJ1gQAAAAAQGkIV2CANlyv91B7c1cAAAAAACpPbZS5Rx99NC688MK46667Yv78+TF+/PiYOXNmHHLIIbHnnnsWfNy///3v8dOf/jTuueeemDdvXjQ2NsaWW24Z73nPe+Lggw+O+vr6or4O1s65Kylcmbn5uiVZDwAAAAAApVHW4cof//jH+PznPx8tLS1d2+bOnRu33HJLdjnssMPiy1/+ct7HvfTSS+P000+Ptra2rm3pOe67777s8utf/zoLdCZOnFi010LpbbiuofYAAAAAAJRxW7CHHnoovvCFL2Shx/bbbx+XXXZZ3HnnnfGrX/0q9tlnn2yftO2KK67I67h33HFHnHbaaVmwsvnmm8cPfvCDuO222+Laa6/Nwprq6up48MEH4/jjjx+iV8baVLkiXAEAAAAAqDxlG65873vfi5UrV8Ymm2wSl1xySey2224xYcKELGj5/ve/H7Nmzcr2O+ecc2Lp0qUDPu4FF1wQHR0dMWnSpCyYecc73hHrr79+zJgxI6uC+cQnPpHtl4Kce++9d8heH8Nv8sRRUVvT85/M83OXRntHR8nWBAAAAADA8CvLcOWJJ56IW2+9Nbv9yU9+MpqaelYcVFVVxcknn5xVmSxcuDD+8Ic/DPjYDzzwQHadql9ytf368Ic/3GtfykNNdXVMXa16pbmlPeYuXFGyNQEAAAAAMPzKMlxJbbo6Q5S3v/3tOffZYIMNYptttslu33TTTQM+dgpkktbW1pz319bW9tqX8jFt/d6twZ5/eeCVTwAAAAAAjHxl+e3/ww8/nF1vuOGG/Q6V33bbbbPrNCNloHbYYYfs+pZbbokFCxb0uv/qq6/uur3zzjvntW7WfhutP7bXtueEKwAAAAAAFaUsw5UXXnghu542bVq/+6XwJZkzZ06flSir+9znPhcNDQ3xyiuvxOGHH561H3v55Zfj8ccfj+985zvZDJfkwAMPjJkzZw76tbB22WhSjsqVuYbaAwAAAABUktd7WJWRzoqSddZZp9/9xo59tQohDahfvHhxv1UunXbccce4+OKL45vf/GZW8ZJmunQ3fvz4+NSnPpUFL5SfqeuP6bXtuZeXlGQtAAAAAACURlmGK6tWrcquU4VJfxobG7tuNzc3D/j4S5cujaam3hUMyZIlS7JB9ql6ZqONNoqhMmHC6GymDGm2TVXX9cSJuT+XYknHnzC2IRYsefV3LJm7cGU0jq6P0Y11Q/rcwMg+fwDlw7kDKJTzB1Ao5w+gUM4fQ6csw5WampohO/ZPfvKT+Pa3v53dnjVrVla5suWWW2aBy5///Oc466yz4rrrrou77747Lr300th8882HZB21tUP3GkeqFDbV1Ax94LTZ1HViwSMv99j2zJwlMXOL9Yb8uYGRff4AyotzB1Ao5w+gUM4fQKGcP4qvLMOVUaNGDagaZeXKlV2311Tlkjz55JNx5plnZrcPPvjgOOWUU7ruSy3F9ttvv9h9993joIMOirlz52b3X3LJJTEUWlvbVK68JqWu6b1I7d3a2zuG/Pm22HCduHe1cOWfzy6IbTZdc1s5oLLPH0B5cO4ACuX8ARTK+QMolPPH62pqijuCvizDlc5ZKqlFV3/SnJXOSpc1zWdJrr766mhra8vaiZ144ok599lggw3imGOOiVNPPTXuvPPOePrpp2PTTTeNYluwYHnRjzlSpXK2lLqmk8P8+UM/XH79dXoHcQ8/NS/+ZeaUIX9uYGSfP4Dy4NwBFMr5AyiU8wdQKOeP102a9GpuUCzFjWrWEptttll2PXv27H73e/HFF7PryZMnR3X1mt+KFJQkW221VYwZ03uweafddtutR7UL5WWTKb3/ET49x1B7AAAAAIBKUZbhyvTp07Pr5557LpuF0peHHnoou95mm20GdNyWlpYBtRvrLp99GRnWHdcYTY09i77mzFseq5rbSrYmAAAAAACGT1mGK3vttVd2nVp43XrrrX1WrTz88MPZ7be+9a15VcQ88cQT8fLLPWdudHfPPfd03d5iiy3yWjtrv9SjcPXqldSt8LmX+w7yAAAAAAAoH2UZrmy00Ubxxje+Mbt97rnn9pq9kob3nH766dHe3h4TJkyIfffdd0DHfe9735tdt7a2xmmnnZY9fnUpdDn//POz2zNmzMhaiFEZrcGefPHVGT4AAAAAAJS3sgxXkv/4j//I5qikOSmHHHJI3H777TF//vx48MEH49hjj40bbrgh2y/dHj16dI/Hzpo1K7ucdNJJPbbvsMMOccABB2S3r7/++jjiiCPitttui3nz5sWcOXPimmuuiQ9+8INZwFJXVxdf/epXh/EVM5w2mzKu17YnXlhUkrUAAAAAADC8eg6OKCPbb799fPOb34yvfOUr8dhjj8WRRx7Za5+Pfexj8ZGPfKTX9qeeeiq7njRpUq/7TjnllGz2ym9/+9u46667ssvqmpqa4owzzohddtmlaK+HtcsWU9fpte1x4QoAAAAAQEUo23AlSVUm2223XVx00UVZCJIqTFKVysyZM7Nqln322SfvY9bX18eZZ54Z+++/f1x11VVx3333ZcdNlSqpHdmee+4Zhx12WEyePHlIXhNrhwljG7LB9vMWr+zatmDJqpi/eGVMHNdY0rUBAAAAADC0yjpc6Zx7kqpI8vHoo4+ucZ+3vOUt2YXKteW0dWLeQ6+HK53VK7sJVwAAAAAAylrZzlyBobal1mAAAAAAABVJuAIF2mJqrqH2i0uyFgAAAAAAho9wBQo0bdKYqK/r+U/o2ZeWRHNLW8nWBAAAAADA0BOuQIFqa6pj8w16Vq+0tXfE03OWlGxNAAAAAAAMPeEKDMIWOeauPGHuCgAAAABAWROuQJHDFUPtAQAAAADKm3AFBmGLDXMNtV8UHR0dJVkPAAAAAABDT7gCgzB2dH1Mnji6x7bFy1tizvzlJVsTAAAAAABDS7gCgzR9Wu/WYA89vaAkawEAAAAAYOgJV2CQtt10Yq9tDz09vyRrAQAAAABg6AlXYJC22WRCr22PPLsw2trbS7IeAAAAAACGlnAFBmlcU31stP6YHttWrGqNp19cUrI1AQAAAAAwdIQrUATbbtq7ekVrMAAAAACA8iRcgSGbu2KoPQAAAABAORKuQBFMnzY+amuqemx7/IVFsaq5rWRrAgAAAABgaAhXoAga6mtiy6nr9NjW1t4Rjz2/sGRrAgAAAABgaAhXoEi2ydEa7MGnzF0BAAAAACg3whUYwqH2/xCuAAAAAACUHeEKFMmmU8bG6IbaHttmv7IsXpq/vGRrAgAAAACg+IQrUCQ11dWxw5br9tp+3z9fKcl6AAAAAAAYGsIVKKKdt5rUa9u9/5xbkrUAAAAAADA0hCtQRNttNjFqa3r+s3ri+UWxeFlzydYEAAAAAEBxCVegiEY11PYabN8REfc/rjUYAAAAAEC5EK5Ake201Xq9tt33mNZgAAAAAADlQrgCRbbjlutF1WrbHnx6Qaxsbi3RigAAAAAAKCbhChTZOmMaYoup6/TY1trWHv94cn7J1gQAAAAAQPEIV2AI7DS9d2uwux9+qSRrAQAAAACguIQrMAR2nj6p17b7H58Xy1e2lGQ9AAAAAAAUj3AFhsDkCaNj8w3H9WoNds+jBtsDAAAAAIx0whUYIm/abkqvbX/9x5ySrAUAAAAAgOIRrsAQ2XWb9aOmuqrHtkefWxivLFpRsjUBAAAAADB4whUYIuNG18fMzSb22n7XQwbbAwAAAACMZMIVGEJvmtm7Ndgd/5gTHR0dJVkPAAAAAACDJ1yBIbTjlutFY31Nj20vzlseT724pGRrAgAAAABgcIQrMITq62pilxnr99p+y73Pl2Q9AAAAAAAMnnAFhtieb9iw17a7Hn45lq5oKcl6AAAAAAAYHOEKDLEtpo6LjdYf02Nba1t73P7AiyVbEwAAAAAAhROuwBCrqqqKvXee2mv7Lfc9H+0G2wMAAAAAjDjCFRgGe2w7JUY19BxsP3fhyvjHk/NLtiYAAAAAAAojXIFh0FBfE2+ZuUGv7TcbbA8AAAAAMOIIV2CYvD1Ha7AHnpgXz89dWpL1AAAAAABQGOEKDJMN1m2KbTed0Gv77+58piTrAQAAAACgMMIVGEbv3n2TXtvufujleHnhipKsBwAAAACA/AlXYBilypVNp4ztsa29oyNuuOvZkq0JAAAAAID8CFdgGFVVVcV737Rpr+23PzA7Fi5dVZI1AQAAAACQn9ooc48++mhceOGFcdddd8X8+fNj/PjxMXPmzDjkkENizz33LPi4zc3N8fOf/zx+97vfxVNPPRXLli2L9ddfP9785jfHUUcdFZtu2vsLdEh2mr5ebLDu6Hhx3vKuba1tHXH9nc/Gh/fZqqRrAwAAAABgzao6Ojo6okz98Y9/jM9//vPR0tKS8/7DDjssvvzlL+d93NmzZ8eRRx4ZTz75ZM77Gxsb47vf/W7svffeMVTmzl0yZMceaSZObIqamupoa2uP+fOXxUjwl7+/GBdd93CPbbU1VXHa0XvEeuNHlWxdUGlG4vkDKD3nDqBQzh9AoZw/gEI5f7xu0qSe4xoGq2zbgj300EPxhS98IQtWtt9++7jsssvizjvvjF/96lexzz77ZPukbVdccUVex12xYkUcccQRWbBSV1eXhTd/+MMf4uabb47TTjstq4xZuXJlnHDCCVkIA7nsvu3kWG+dxh7bUvXKNbflDuwAAAAAAFh7lG248r3vfS8LOTbZZJO45JJLYrfddosJEyZkQcv3v//9mDVrVrbfOeecE0uXLh3wcc8///x45plnorq6Os4777z49Kc/HRtvvHFMnTo1DjzwwOy5amtrY/ny5Vl4A7nU1lTHAXtu3mv7nQ++FM/MUZUEAAAAALA2K8tw5Yknnohbb701u/3JT34ympqaeg0VP/nkk7OAZOHChVnlST5zVpKDDjoo9tprr177bL311rHHHntETU1NPPLII0V5PZSn3badHJtM7l2K9qtbHy/JegAAAAAAqOBw5bbbbusKUd7+9rfn3GeDDTaIbbbZJrt90003Dei4d9xxRyxatCi7ffTRR/db3fLggw/GxRdfXMDqqRTVVVXxb2/fotf2B59eEPc//kpJ1gQAAAAAQIWGKw8//Oqg8A033DAmTpzY537bbrttdp2CkIF44IEHsuvUAmyjjTbqcV+a7dKpvr4+C3ZgTbbbdGJst1nv39Erfv9YrGppK8maAAAAAACowHDlhRdeyK6nTZvW734pfEnmzJkTra2tazzuP//5z+x60003za7vueee+MxnPhO77LJLzJw5M3bfffc48cQT46mnnirCq6BSHPS2LWL1LG7e4pXx2788XaolAQAAAABQaeHKggULsut11lmn3/3Gjn113kVHR0csXrx4jcedO3dudj1+/Pis9dehhx6atRRbsuTVAeRpfsu1114b++2334BbjcHGk8fG3jv3DgJvvPvZeGHu0pKsCQAAAACAvtVGGVq1alV23dDQ0O9+jY2NPYbVr8myZcuy67vvvjuuu+66mD59enzxi1+M3XbbLWsLdsstt8QZZ5wRr7zySpxwwgnxy1/+MmbMmBFDYcKE0VqPvaa6uqrreuLEphiJPv6BmXHvY3NjwZJXf3eTtvaOuOKmf8Y3P/WWqHntNQLFVQ7nD2D4OXcAhXL+AArl/AEUyvlj6JRluFJTUzMkx12xYkVXBcsWW2wRV155ZYwZMybbNmrUqNh3331j++23jwMPPDCWL18eZ599dlbhMhRqa4fmNY5kKWyqqRmZIcS4MQ1x9H7bxxmX3dNj+yPPLIjf/PmJOOgd00u2NqgEI/n8AZSOcwdQKOcPoFDOH0ChnD+KryzDlRR0DKQaZeXKlV2311Tl0v24yfHHH98VrHS3+eabZ+HKZZddFrfddlsWsowePTqKrbW1TeXKa1Lqmt6L1N6tvb0jRqo3zZwSO02fFPc99mr7uU4/u/GReMOW68UW08aXbG1Qrsrl/AEML+cOoFDOH0ChnD+AQjl/vK6mprhTUsoyXOmcpdI5C6UvnXNWUqXLmuazJE1Nr5dNpeH1fdl1112zcCW1Cnv22Wdj6623jmJbsGB50Y85UqVytpS6ppPD/Pmvtm4bqT6895bx8NPzY2VzW9e21raOOPOK/4uvHrFrNNSpWIJiKqfzBzB8nDuAQjl/AIVy/gAK5fzxukmTXs0NiqUsB9pvttlm2fXs2bP73e/FF1/MridPnhzV1Wt+K6ZOnTqgSpfuFS2d819gINYbPyo+8s7eLcBenLc8rrzpsZKsCQAAAACACghX0qD55LnnnoulS5f2ud9DDz2UXW+zzTYDOm73/dKx+5IG2ndKwQ3k480zp8QuW6/fa/uf//Zi3Hr/CyVZEwAAAAAAZR6u7LXXXtl1W1tb3HrrrX1WrTz88MPZ7be+9a0DOu7b3va2rts33HBDn/v95S9/ya432GAD4Qp5Sz0QD//XGTF+TH2v+674/WPx+POLSrIuAAAAAADKOFzZaKON4o1vfGN2+9xzz+01eyUN7zn99NOjvb09JkyYEPvuu++AjrvlllvGzjvvnN2+6KKL4sknn+y1z/333x+/+93vstv77befofMUZMyouvjkB7aLmuqevz9t7R1x3n//PeYvXlmytQEAAAAAVLqyDFeS//iP/8jmqDz99NNxyCGHxO233x7z58+PBx98MI499tiuypN0e/To0T0eO2vWrOxy0kkn9TruKaecks1bWb58eXz4wx+OK664Ipvt8tJLL8XPfvazOPLII7NB9tOmTYujjz562F4v5WfGxhPiQ3tv2Wv7omXNcdYv7o+lK1pKsi4AAAAAgEpX1ZHKOMrUNddcE1/5yleitbU15/0f+9jH4uSTT+61fcaMGdn1brvtFpdddlmv+++888743Oc+F4sW5W7PlIKVH/7wh7HVVlvFUJk7t2c1TiWbOLEpamqqo62tPebPXxblJP3zvOi6h+OOf8zpdd8WU8fFFw/eKRrqakqyNigH5Xz+AIaOcwdQKOcPoFDOH0ChnD9eN2nS2Cim2ihjBxxwQGy33XZZC6+77ror5s2bl1WpzJw5M6tm2WeffQo67h577JFVvlxyySVx8803x/PPP59VyaR2ZO9+97uzipZx48YV/fVQufNXZr+yLJ6e0zNQe+KFxVmLsGMP2D7qagUsAAAAAADDpawrV8qZypXKSl8XL2uO0y7/v3h5wYpe92236YT47IE7qGCBAlTC+QMoPucOoFDOH0ChnD+AQjl/DF3lStnOXIFyMq6pPk740I6xTlN9r/sefHpBnP3Lv8WKVbnb3wEAAAAAUFzCFRghJo0fFcd/8A0xqqF3N79Hn1sY3/7ZvbFgyaqSrA0AAAAAoJIIV2AE2Xjy2PjiwTtGU2PvgOXZl5bGqZf8bzyz2mwWAAAAAACKS7gCI8xmG4yLEz+8U4wZVdfrvoVLm+NbV/xf/PUfc0qyNgAAAACASiBcgRFawfLvH9k5Joxt6HVfc0t7/Ph/HoqfXv9INLe0lWR9AAAAAADlTLgCI9TU9ZriKx/dJTaZMjbn/X/+2+z4+iX3xJOzFw/72gAAAAAAyplwBUaw8WMa4uRDdo6dtlov5/2zX1kW37zsnrjq1sdVsQAAAAAAFIlwBUa4hvqa+MwB28eBe20e1VVVve7v6Ii4/s5n48sX3hX/9+jc6EgbAAAAAAAomHAFykAKVd77pk3jpEN2ivFj6nPu88qilXHef/89zvz5/fHUi1qFAQAAAAAUSrgCZWT6RuPjlI/vFrtts36f+zz8zII49ZJ74tyrH4hn5iwZ1vUBAAAAAJSD2lIvACiusaPr45h9Z8auW8+Ny37/aCxe1pxzv/v++Up22WaTCfGuXTeK7bdYN2dbMQAAAAAAehKuQJl644xJsc0m4+PXtz8VN//fC9Hex6yVVMmSLhusOzrevtPU2GO7KTFmVN2wrxcAAAAAYKQQrkAZG91YF4fsMz32esOG8YubH49/PDW/z31fnLc8fnbTP7P93rDlevGWmVOyapbaGt0DAQAAAAC6E65ABZg6aUx84UM7xqPPLoj//vOT8djzi/rct629I+59bG52GdVQG2/Yct3YeatJMXPzidFY75QBAAAAAOCbUqggMzaeEP/+kZ3jsecWxo13Pxd/e/yVyN0s7FUrVrXGnQ++lF1SBcuMjcfHtptMiG03nRgbTR5jRgsAAAAAUJGEK1BhqqqqspAlXebMXx5/+N/n4i9/fzGaW9v7fVxrW3s8+NT87BLxRDQ11sZW08bHFlPHxeYbjItNNxiXVboAAAAAAJQ734RCBZsycXQc9q8z4sC9toh7Hn05bv/7i/F4Py3Dulu2sjXuf/yV7JKkGpYNJzXFZhuMi2mTxsTUSU3Z9TpN9UP8KgAAAAAAhpdwBYjRjbWx5xs2zC4vzV8ed/xjTtz7z7nxwtxlAz5Gai+W9l/9MWNH18XU9Zpi8sTRsf74UTFp/KhYf8Kr1ypdAAAAAICRyDebQA8pBNl/z82zSwpa7vvnK1nQ8uQLi6O9o78JLbktWd4Sjzy7MLusLgUvKWSZMKYhxo9tiAnp0u12qnpprK/JWpkBAAAAAKwthCtAv0HLrN03zi7LV7bGo88tiIefXhAPPbMgZr8y8KqW/oKXdOlPbU11FsKMGfXqJd0eO6o+xoyuy+a+pOqX1y81Mar+9dvpsYIZAAAAAKDYhCvAgFuH7bTVpOySLF3REk/OXhxPzl6UXT/14uJsDkuxtba1x4Ilq7JLvmqqq7qCloa62mioq4662uqor6uJ+tWuc21Pj08BTU3Nq9e11VVR0/lzdXXU1rz6c+f27OfXtr8a7IRwBwAAAADKUFVHRwF9fii5uXOXlHoJa42JE5uyL7bb2tpj/vzBV1NQmHQqeXnBinh+7tJ4Ppu98ur1SwuWRyWfZVK2Ul1VFdXVVa9dR1RF588RVZ3bX7uv+75VObalx6Tbrx771evsx7R/tvHV42fBTrd9OjOe9PNru3c9psd9rz0uO0rn7ddCotf3Xe34OfKj1TdVDWCnnDFUr3167zWQ/Kqqj+M0NtZln0FHe0esXNVSsvUAI8uoxvquc8eKlc2xdnKigbXRqFF12X/TpXa7K1b0X8E9EjjTwPCeP7r++6MMzh/A8Kivq443vWFqzNhkou9OI2LSpLFFPZ5wZYQSrrxOuLJ2a25pi5cXroi5C1Zk191vz1u0MtranYIAAAAAYCikP8o96bBdY4+ZUyr+u9NJRQ5XtAUDhlRqsTVt0pjssrq29vZYtLQ5FixdFQtfa/3V/faSFa/OZFm6vCX76z4AAAAAYODS3zVfe9sTWbhCcQlXgJJJ80kmjmvMLv1JBXYrVrVmQUsKXFLYsmR5czbjZWVzayxf1RorV7XFiubWbL8Vq9p6bF/V0jZsrwkAAAAA1iaN9WKAoeBdBdZ6aa7H6Ma67DK5gMenCpnmlvZobk3XbV3XLd1/bm3L9unclq5b2zuydnOtbR3R2t4ebW2v/dzeEa1tr/7cub31tf3auv2cqm3a29NfCHRkl9QbN/21QHt2/dql/dXwKG1TmwMAAABAMTXW18SH3jm91MsoS8IVoCIqZEY1pEus1bKQpXsgkwKXjtUCmdeuUxKTwpgskEnBzatX2f6vber3vuw6/e+1292P+er16/elx/U6Xud+Odq1rb6l9y49N+Tq+LaGh2Tr6/8BA1vHmDGNUV1dlb2vS5as7H2QNR6z/0gs92sTo8FIN6bp9XPH0mVrPncMO6cZWGs1jWmI6urqaG9vj2VLV8VI5lQDw2tMU0O3//4Y2ecPYPjU19bE7jtsEBPGjcr+YJjiEq4ArEUVOjXpUl3qlVSOiROboqamOvsPjEof6gYMnHMHUCjnD6BQzh9AocY1reV/bTyC+QoPAAAAAAAgD8IVAAAAAACAPAhXAAAAAAAA8iBcAQAAAAAAyINwBQAAAAAAIA/CFQAAAAAAgDwIVwAAAAAAAPIgXAEAAAAAAMiDcAUAAAAAACAPwhUAAAAAAIA8CFcAAAAAAADyIFwBAAAAAADIg3AFAAAAAAAgD8IVAAAAAACAPAhXAAAAAAAA8iBcAQAAAAAAyINwBQAAAAAAIA/CFQAAAAAAgDwIVwAAAAAAAPIgXAEAAAAAAMiDcAUAAAAAACAPVR0dHR35PAAAAAAAAKCSqVwBAAAAAADIg3AFAAAAAAAgD8IVAAAAAACAPAhXAAAAAAAA8iBcAQAAAAAAyINwBQAAAAAAIA/CFQAAAAAAgDwIVwAAAAAAAPIgXAEAAAAAAMiDcAUAAAAAACAPwhUAAAAAAIA8CFcAgP/P3p3A2VmXd8O/ZsnsCWQjK5AQILLLolTEwgNYqCwKrshjlUXcsNoH5UWo2moRxFJKbRElKNoiKhQREAU0gChSKotsYU9CNrKvM5l93s99h5nMzDmTzExmcs6Z8/2+7/mc+/zPvfzPZLj7eH5z/S8AAAAABkC4AgAAAAAAMADCFQAAAAAAgAEQrgAAAAAAAAyAcAUAAAAAAGAAhCsAAEBR+p//+Z+YPXt2+rj44ouH7TqLFy/uus5HPvKRYbsOAACw8whXAAAAAAAABkC4AgAAAAAAMADCFQAAAAAAgAEQrgAAAAAAAAyAcAUAAAAAAGAAygeyMwAAQD7p6OiI3/72t/HAAw/Ek08+GStXroxNmzZFTU1NjBs3Lg455JB417veFccee+yAz/2Rj3wkHn300Zg2bVrMnTs3Pe8Pf/jD+PWvfx2LFy9Or73nnnum5072nTBhQr/PvWzZsvjRj34Uv/vd72Lp0qVRWloaU6dOTc/1oQ99KL3m9jz99NNx9913x5/+9Kf0fOvWrYtRo0bFLrvsEm9605vi//yf/xOnn356VFRUDPizAwAA2yZcAQAACtIrr7wSn//85+PFF1/MeG/Dhg3pY8GCBfGLX/wi3vGOd8Q111wTtbW1g7rWokWL4rzzzkvP193zzz+fPv7rv/4rvv3tb8dRRx213XP9/Oc/j3/8x3+MzZs39xhPPkfyuOmmm+Kb3/xmvPOd78x6fBLyXHzxxXHfffdlvNfS0hINDQ1p2HL//ffH9ddfnz5mzpw54M8MAAD0TbgCAAAUnOXLl8eHP/zhtFojMXHixDjmmGPSio+kCiQJFx566KFYsmRJ+n6yfdVVV8VXvvKVAV+rsbExPvnJT6bBSlIFcsIJJ8Q+++wTq1evjnvvvTdWrFiRBh7nn39+fPe73423v/3tfZ7rmWeeSathElOmTInjjjsudtttt3S+SUVM8nnq6+vji1/8Ytxxxx2xxx579Di+vb09DXmeeOKJ9HVVVVX6uffee+90e+3aten5k+t0hkKf+9zn4vbbb09/LgAAwNAQrgAAAAXnX/7lX7qClb/8y79Mq0aScKG71tbWuOKKK+I///M/uypGLrroooz9ticJUZLH7rvvnoYns2bN6nrvwgsvTKtI7rnnnrRq5Ktf/Wq6VFdfS3ElVSUlJSVxwQUXxKc+9akoKyvrei+pwvnYxz6WVsIkVS033nhjRhiUfIbOYCUJkpKlxaZPn55xnV/+8pfxhS98IQ1jXnjhhXjsscfiLW95y4A+NwAA0Dd/ugQAABSUJHhIqjwSlZWVcfnll2cNTMrLy9MwZcyYMV3Bxquvvjqoa1ZXV8cNN9zQI1hJJL1dkqBn//3376oUueWWW7Z5rqSnShKudA9WEmPHjo1LLrmk63XSS6W3JFzpdOmll2YNVhInn3xyuhRap2effXa7nxEAAOg/4QoAAFBQkgqRJFhIluFKQoptNZJPKkj22muvrtfJkluDkSxBljSvzyYJcT7zmc90vU6WCtuWZFmvvhx++OFdVS9Jo/tswcxnP/vZ+OAHPxjHHnvsNq8ze/bsru1k2TIAAGDoWBYMAAAoKEklygc+8IF+7bt48eK0YqX7UmGDkVSCbEuyNFkSsiTnTypOkj4t2appJk+e3Ge1SSI5R1LBkvSUyRYEnXLKKf2a7/r169Nz7OjnBgAAshOuAAAABS8JEpKG86+99lr6ePnll2PevHlpo/juOjo6BnzuUaNG9agCySapNkmazyfLjiVBRtLkvncz+sT48eO3e70kYEkk/VL6E6J0/9zJ9ZOeLa+88kqPzzqYzw0AAPRNuAIAABSkpMn8nDlz4s4774yVK1f2uV/S26StrW2HKmU6A49t2WWXXbq2V61alTVcqa2tjR3V3NwcP/nJT9LeLi+++OKwfW4AAKBvwhUAAKDgPPbYY/HpT3861q1bl1FBMmPGjNh3333jzW9+c7z97W+Pr371q/Hoo48O+lr9CVYS3YOMpNplOCQhUtKzJalO6a60tDSmTZsW++yzTxx00EFx5JFHxu9///u49tprh2UeAABQ7IQrAABAQVm7dm3a1L0zWNlvv/3i//7f/xuHHXZY2nQ+qdjobvPmzTt0vY0bN/Zrv2SJrk4TJ06M4fCFL3yhK1hJlhj72Mc+FkcddVQaqlRWVvbY97e//e2wzAEAABCuAAAABSZZDitZEixxwAEHpEtkJRUrfVmzZs0O9R5paGiI119/PW1G35ckwFm0aFG6XVNTExMmTIih9uc//zkeeeSRrmv89Kc/jd13332bIRQAADA8SofpvAAAAMMiCRk6vec979lmsLJ48eJYsmRJ1+v+NInP5ne/+90237///vu7zv2Od7yj30uJDcSTTz7ZtZ0sd7atYCUJkbovhTbYzw0AAGQnXAEAAApK0tC9v9UZl19+eY/Xra2tg7rmDTfcEI2NjX3O5zvf+U7X65NOOily/bl/9KMfpcHSjn5uAAAgO+EKAABQUN70pjd1bd98883x2muvZeyThA+f+9zn4je/+c2Q9F9ZsGBB/O3f/m1s2LAhox9LMv7iiy+mr5O+L3/9138dw/25H3vssbjvvvuyBjDXXXddfPOb3xzSvjMAAEBPeq4AAAAF5QMf+ED88Ic/jKampjREOfnkk+Ov/uqvYubMmWm48Oqrr8aDDz7YVekxatSoaGlpSbfXrVs3qGsm50jOmVznxBNPjClTpsSyZcvinnvu6aoiGTduXPzTP/1TlJSUxHDobFz/0ksvpct+XXDBBXH00UfH/vvvnzazT5Y/S5Yn65zPUHxuAAAgO+EKAABQUJJeI1dddVV84QtfSJfqSkKUu+66K2O/JORIgpik6f1XvvKVdOzZZ58d1DWT5cWS4CQJLn7yk59kvL/33nunFSPb6oOyo8rKyuLb3/52nHPOObF06dJ07Pe//3366O2II46Iv/u7v4uzzjprhz43AACQnXAFAAAoOO985zvjjjvuSCtY/vjHP6ZhQ1tbW9TW1sYee+wRhxxySLz3ve+N/fbbL5YvXx6lpaVpU/dkKa1LL700ampqBnS9Qw89NO6+++6YM2dO/Pa3v02rVqqqqtLzn3LKKfGe97wnKioqYrgl1Tm/+MUv4r/+679i7ty5MX/+/HTJr+rq6rSaJpnPu971rjj22GPTcGmvvfZKK3mSpdMef/zxdNkyAABgx5V0JPXkAAAA9PCRj3wkHn300XQ7CVSmT5+e6ykBAAB5QkN7AAAAAACAARCuAAAAAAAADIBwBQAAAAAAYACEKwAAAAAAAAMgXAEAAAAAABgA4QoAAAAAAMAAlHR0dHQM5AAAAAAAAIBipnIFAAAAAABgAIQrAAAAAAAAAyBcAQAAAAAAGADhCgAAAAAAwAAIVwAAAAAAAAZAuAIAAAAAADAAwhUAAAAAAIABEK4AAAAAAAAMgHAFAAAAAABgAMoHsjP5Y+XKjbmeQt4YO7YmysvLorW1Ldaubcj1dIAC4v4BDIZ7BzBY7h/AYLl/AIPl/rHVxImjYyipXKHglZSU9HgG6C/3D2Aw3DuAwXL/AAbL/QMYLPeP4SNcAQAAAAAAGADhCgAAAAAAwAAIVwAAAAAAAAZAuAIAAAAAADAAwhUAAAAAAIABEK4AAAAAAAAMgHAFAAAAAABgAIQrAAAAAAAAAyBcAQAAAAAAGADhCgAAAAAAwAAIVwAAAAAAAAZAuAIAAAAAADAAwhUAAAAAAIABEK4AAAAAAAAMQHnkuTVr1sT1118f999/fyxZsiSqq6tjr732itNOOy0++MEPRllZ2aDPvWDBgvj+978fDz/8cCxfvjxqampi5syZ8a53vSs9d2Vl5YDOt2LFijj11FNj3bp1cfnll8cZZ5wx6LkBAAAAAAD5Ka/DlUWLFsWZZ54ZK1eu7Bprbm6OJ554In3ccccdMWfOnKirqxvwue++++64+OKLo6mpKeu5f/zjH6ehzu67797vc15yySVpsAIAAAAAAIxcebssWENDQ5x77rlpsDJx4sS46qqr0gqTe++9N84///y0YiUJQZJAY6Cee+65uOiii9JgZc8994x//dd/jQcffDDuueeeNHCpra2N+fPnxyc+8YlobW3t1zlvuummeOihhwbxSQEAAAAAgEKSt5UrN998cyxcuDDKy8vjhhtuiNmzZ6fj48ePjwsvvDAmT54cX/va19JA5PHHH4/DDjus3+dOwpSWlpYYO3Zs/Od//mdMmjSp672zzz47pk2bFp/97GfjlVdeSc9/8sknb/N8yX5XXnnlDnxaAAAAAACgUORl5UpHR0fceOON6fYpp5zSFax0lywXNmPGjHT7lltu6fe56+vr0wqYxHvf+94ewUqnE044Ie2/kvjzn/+8zfMllS1JFUxjY6MeKwAAAAAAUATyMlyZN29e2hw+cfzxx2fdp7S0NI477rh0e+7cuWkg0x/Jkl+PPPJI/OxnP4u/+Zu/6XO/kpKS9DmpnNmWf//3f49nnnkmDjrooPjkJz/ZrzkAAAAAAACFqzxfw5VOBxxwQJ/77bfffulz0kR+8eLF/W4+X1dXF4ccckif7996661phUvi6KOP7nO/pOfL9773vaiqqopvfvObaR8YAAAAACgG3f/YucefPXd70dHtRV9/G91zPPv+gz1/n+fuc5+Bfr7sJxro+bPt2/2z9XXN/ly/z2P7mFjWn/swnLvnaQb2e5LtZ7Njv4MD+FlkOVG2o7OeMdvvaO/BrPtse2597VVRXhaH11VGTXVFttkwEsOVJUuWdFWNJL1V+jJ16tSu7YGEK70l/VfWrl0br776avz3f/933Hnnnen4u9/97jjqqKOyHpOEL8lyYG1tbfH//X//X8yaNSudAwAAAPT+wib5AqStrT3a0+e2aG5pS78C6XxvyxckHen7ifZ08I333/gCpfOLny1vbXm//Y2BNw7vOufW/bb9/pbhLXPofe6tx3R/P/u5u++79TpvnL3XudJ5d3vvjbeyfr7sc+j1fufPsdtn7JpXRz/f7zHvvn9+7b3fG9DPro/3s8xr679P7+t1+zlufbvHZ+nxNV2vn9HW38luh3d+pn4e0+P3YOvQ1s/Xa17dz5/tHD2P3/qiaw49zrf1xH39nLIe08fPKXPf/s+r+79Dz8+1dYeO7f3stvHv0PuYzhVWkuH2zhvFYH8/sn1xu50vrXttAgWkrnpUfP0TR8XMqWNyPZURJy/DlSTo6Kww2VY1yOjRo7u2169fP+jr/eIXv4hLL72063Xyf7AuvPDCOPfcc/s85hvf+Ea89tpr8Rd/8RfbXF5suIwdW9P1f1iLXWlpSdfzuHG1uZ4OUEDcP4DBcO8oPsmXWsn3WFu+BN+6nXy5lW28o33LF7CdY+l2+5Yvs7aMb32/czs5V+eX5z332TrWuU/v8XT7jbm0Z8yl23y7H9Nj7pnHZVwr+f/at35R3BUI9AgHth7TPRzIfL3lW7z0Whnn67xOr/NmuU7meM/zdb9O1vm88Ub7ts7XfV7b+dxZ59nrC0sAgJ1t0+aWuOme5+Mr5x7pf78USrhy7bXXxjXXXDOgY04//fS44ooroqmpKX1dWVm5zf2T5bg6dR4zGEuXLu3xOvl/BN9www1ps/pPfepTGSHGb3/723TpsCTcufzyy3MScpSXW4Kst+TfoaxM4AQMnPsHUEj3jq4v7Ns7oq29/Y3njq7ntrYtX553vtc9AOjcr8cX9Z3HdoUFnV+8J6/fuE7nF++9ju88d8/X3cYz9s1ybDqPN+bW7b3uoUP397bMI8s1+5hDtqChK0hIvsTvHSr0CBe2fjEPAACFalNDs+8+iqVyZWf3Lnn/+98fZ599dlRUVMTTTz+dhkKPPvpo+rxmzZr4+7//+659V61a1fU6qXbpvjTZztTa2qZy5Q3JX40mP4vO/xEM0F/uH1DYtgQF7dHalgQK7dGaBgtbX6dBQ3tHtCbbbR3R2r7luWuf5PUb72cGEx3R/sY5Ol+n7yWvk2V72rcs75Me29HtvTe2t1x7y3vtXa+7BQW9gpHM97bu0xWIdNsXAACgv/76qBm++4gkdygtjHDlzDPPjBNPPHFAx3Qu81VdXd2vapTGxsasVSwDNWXKlK7tI444In7wgx+kYUsSsNx0003pZ0l6qiSSYCUJXE444YS00iZX1q5tyNm1801SzpakrsnNYc2a+lxPBygg7h+wRfLfQEsaQGwJHZLAYMvjjWAieb/1jfffCCO675eECVuOz3JstxCj69Et+Oix/UaA0bV/72O7hRbJdnH/zwIAIJ90/flrSfL/b3nV/W9it24nf+DV7Ziu7fTAHufast/W5UhLsvRg6X7+rZfYum/3c3Y/psccMj9Fj7n3vk63T5Jxkh6Hdb9eH+fouXv2/fs8fx/zzXZst59In+frOa/+n7vf5+9xbOZn7c/PpY9T9Ovn3td8+7zuduYwZP+OQ/x7MtjfkR39Pelrzlk/RrafZz8OzHauHnPOslPFqNI46pBp8eZ9d0v/t1exf/cxceLWNiN5Ha6MHTs2fQzGmDFjuprGZ/s/GJ02btzY43pDpby8PD7/+c/Hhz/84fSvIR944IE0XPnJT34S999/f4wbNy6+/vWvD9n1AIDiDTSS0CJ9vLHd2vm6ta3n+9322dbr5PjeAUePIKQrHNk6rh8AwNYvOUvf+N+fyf8OTb+sfOOL0sztN77w7NzuduyW1kzdjnnji87y8tKu8yZVbZ1fnKb7d9sv67W3TOqN99+Yc0nme51f7Hb/4rRzrj2O69q3j/N2f7/HHLZ+Cbz1mL7m0XPf7nPr/GzZ3ts61+3Ma5vz3vqZs86rpJ/vD3jeW7/myvzZbO9n1+vcXdffOpeeX9ZnfqnX/cvu/n7Z39eXrL1/Btnmk+2Y7tfN+hm2O6/M+Ww9puf5S7Z7TPbP3TsU6Pmz3frv2dcx2a67c/4wrNSXo8CA6bNSZMuCzZgxI31uaWmJFStWxKRJk7bbK6V79clQOPDAA7u2Fy9enD7/8pe/TJ+TypW3ve1t2zz+S1/6UvpIvPDCC0M6NwBg+AKP5ta2aG5pj+aWtmhq3fKcPrq226Op2z7d9+/a543nppY3QpIsQYilnWDnKXnjS++uL7nfeC7tGu/5Xte+0e116Zb9t36Z3ev1G+dL9+vx5Xj3/Xqev/ecBjXHHq/7mFPvOaefJcvx3ead7f1tBg7djk9Dhjd+8FtChp5z6is8SKTX6bFf9rHuAUfnF9P9DTiyf4ad8wWpL0cBAEaOvAxX9t13367tefPm9RmuPPfcc12VLtOnT+/XuZ988sn493//91i0aFFcf/31scceewzrkmMAwNBLKluTiovNzW3R9MajMXm0tG7dTsZbkufWLdvdx5paozEJP5p7BiHJOSHXku94y5Ivv0tLtjwnX1Bned25T4/XPba3fone9WV+9/N1/0K+tHuAkG3/yDq+5ditX+B3P2/XPj2O7XautO/V1vey799zzpn7d/+M3eew5TpbwoWd91fFAABA8cjLcGWfffaJadOmxZIlS2Lu3Llx7LHHZuyTLNeVLNGVOProo/v9l0ZJ0/qHHnoo3b7nnnvi4x//eNb9OvdJHHDAAelzEsa0tbX1ee5ly5bFySefnG7/4z/+Y5x66qn9mhMAFJM0FGlqfePRFg1NrdHQ2Pl6y6Oh13Py6ApM3nhOGoVTLEFDadofqaykZMtzGh68MVbax+uy0m7v9XqdbHc/V9mWL+C3BhqlXV/cdwUYb3xhn7weM6Z6y9I+EdFQ35SOJV/wl2UJPXoc322fnmFIt+u8EUAAAACQ3/IyXEn+B+Vpp50W3/nOd+K2226LD33oQ7H//vv32Ofmm2+OBQsWpNtJ8/n+Ss6z9957x8svv5w2rn/Pe94TEydO7LHPqlWr4l/+5V/S7eS94447rl8VLN3fT0Kc2lrr2QEwcgOSJBCpb2yJTZtbon5zt+30uTXqN7f0CEfS7cbWtFKE3ClPAoWy0hiVBAxlJVFeWpqOJWFB5/aW97c8l6ePkq7ndCzZr7zbsd3263HuzkAjDTG2bifHdYYL2wtL8rHqwLI+AAAA5GW4kjjvvPPSYGX58uVpePLFL34xjjnmmHS5rltvvTWtIkmceOKJcfDBB2ccf9FFF8VTTz2Vbv/617/u8d6ll14a5557bqxevTo+8IEPxN/93d/FEUccEWVlZfHHP/4xrrnmmrSfS2lpafzDP/xD1NTU7KRPDQC56TOShCIbGppjY31zbGhoiY0NW56ToCQJSZJHGpgkrxtb0ooTBiYJDEaVl259lGXbLksDiq3jZelzebZjsr1O9n0j3OgRhnQLOlRFAAAAwAgOV+rq6uK6666Lc845J9auXZsGIr0dfvjhceWVV/a5RNf8+fOzvnfUUUfF5ZdfHl/5ylfSECUJbnqrrq6Or3/963HCCScMwacBgJ0raaK+blNzrN+UhCTNmcFJfXNsbNgSqGxqaIliXmArCR4qysuiYlRpVIwqS7cru7bfeH7jdWWP/ba+t2X8jffe2KcyfV3WFYAklRoAAADAyJC34UrnEl533313zJkzJ+290llNMmvWrLSfyVlnnRWjRo0a1LmT5cAOPfTQ+OEPfxh/+MMf0nOXl5fH9OnT0x4uH/3oR2Py5MlD/pkAYEeX40oCk3Wbmt54ZNne2BT1ja0xEiWVF1UVZVFZURZVFeVpgJG87hpLX5en2+l7lVvGOvdP9+t2TBJ+JBUdAAAAAANR0tGhG2whWrlyY66nkDesew6MlPtH0qA9qShZvaExVq9vjDUbmrptN8baTU1ptUkhV4hUV5anj5pez+l2Ved2WTqevtc1Vh7VFeVpBQjkWr7dO4DC4f4BDJb7BzBY7h9bTZw4OoqmcgUARpIkPEmqSlas3Rwr123eEpx0C1LWbGyM1rb8/5uHJPSorS6PuupRUVs1KmqrR0Vd+lyesZ2GJFXJc9I7pCzXUwcAAAAYEsIVABhCLa3tsWr9lvAkCVFWrNscKzuf1yXhSXvkk2RJrDG1o2J0TUWMSR+jYnTtlu3RNaO2BChJYJIGKeVpmKJ3CAAAAFDshCsAMEDJippJY/jXV9fHstUNsXR1fby+uiHdTpbvynXtSdJofde6yti1riJ2qauMXWor3ghMRm0JTd7YTgKVpO9ISYmwBAAAAGAghCsAsI1lvFat2xxLVzXEsjVbgpRlbwQpuWgYn/Qs2RKabAlO0ufRW0OU5PXYuoq0P4nABAAAAGD4CFcAICIaGltj8cpNsWjFpvR5cfpcH00tbTttDsnSW+N3qYrxY6pi3JjKmJA+V3WNJct0CU0AAAAAck+4AkDRLem1dmNTzF+2IVasb4qFr2+M+cvWp31RhlvS3H3i2OrYbdfq2G1sdUxIQpOuMKUqKkdp+A4AAABQCIQrAIxo6+ubY8GyDWmYsuD1jel20i9luCRLdG0JT2p6BCkTd61OK1MAAAAAKHzCFQBGjOaWtjREeXnJ+pi/bGMseH1DrNnQNOTXKSstiUnjamLKuJqYPL4mpo6vTZ8nj6tJ+50AAAAAMLL5BgiAgq5KeXnxunhp8fo0UEmW+Gpr7xiy85eXlca0CbUxbWJtTJ1Qm4YpUybUpst5Je8BAAAAUJyEKwAUjDUbGmPewrXx/MK18dKS9bFiCPukJA3kp0+si913q0ufp+9WF5PHVUdZqRAFAAAAgJ6EKwDkrQ0NzWmQkjyeW7h2yMKUZEmvmZNHx/57jY+99xibBiotjcPXhwUAAACAkUW4AkBe9Ux5YdG6eObVNWmFyuKVm3b4nOPHVMWMKaNj5pQxaaCy5+TRUVO1pbH8uHG1UVZWGm1t7bFGuAIAAABAPwlXAMipVes3x9OvrI6nXlmdBirNre2DPldFeWkaouw9fZfYe9ou6faY2oohnS8AAAAACFcA2Kla29rjlSXr48+vrE5DlSWr6gd9riQ42WfaLmmYss/0XWOPSXUazQMAAAAw7IQrAAy7lta2eHb+2njshRXx5Muror6xdVDnGVMzKt6059jYb8+x6fNuu1ZHSUnJkM8XAAAAALZFuALAsGhsbo2nX12TBipJlUpTc9uAz1FdWR5v2mPXNEjZf8+xMXVCrTAFAAAAgJwTrgAwZFpa29PeKY8893r6nLweiCQ2mTl1TBy81/g4aNb42HPS6CgtFaYAAAAAkF+EKwDskPaOjnhp0br447PL40/Pr4iGpoEt+VVTWR4H7jUuDp41Pg6cOV4DegAAAADynnAFgEFZtro+fv/0svif55bHmg1NAzp28riaOHTfCXHIrAkxa9qYKCvVhB4AAACAwiFcAaDfmlra0uqU3/15aby0eP2Ajt19t7o4fPbEOHz2bjFtQu2wzREAAAAAhptwBYDtem35xnjwz0vjkWeXx+YBLPs1c8qYOOJNE+PwfSfGbmNrhnWOAAAAALCzCFcAyCppRv/ovOXx28cWx4LXN/b7uEnjauJt+0+KIw+YFJMEKgAAAACMQMIVAHpYv6kp7n9iSTzwxJLY0NDSr2OSJvRv3W+3eNsBk2PG5NFRUlIy7PMEAAAAgFwRrgCQWvD6hrjvfxen1Spt7R3b3b+stCQO2XtC/OUhU+KAmeM0pQcAAACgaAhXAIpYR0dHPPXK6rj7kYX9blC/29jq+MtDpsbbD5wcu9RVDvscAQAAACDfCFcAilB7e0f87/Mr4pd/XBiLV27a7v7lZSVx+Ozd0lDlTXvsatkvAAAAAIqacAWgiLS2tcfDz7yeVqqsWLt5u/uPqRkVxx46Lf7PodNUqQAAAADAG4QrAEWgrb09Hn769bjjDwti9YbG7e6/x6S6eOcRu8db95sUo8r1UgEAAACA7oQrACN8+a+kQf0vfj8/lm+nUiVZ6OuwfSfGO9+ye+wzfRdLfwEAAABAH4QrACO0Uf3jL66K2x96NZasqt/mvmWlJfG2AybHX//FHjFlfO1OmyMAAAAAFCrhCsAI8+rSDfGTuS/Fy4vXb3O/ivLStEH9iW/dI8bvUrXT5gcAAAAAhU64AjBCrFq/OW578NV45Lnl2w1Vjjt8epz01j1iTG3FTpsfAAAAAIwUwhWAAre5qTV++ceFce//LorWtvY+9ysvK4lj3jwtTn7bnrFrXeVOnSMAAAAAjCTCFYAC7qvyv8+viJt/+1Ks39Tc536lJSVx9MFT4tSjZlj+CwAAAACGgHAFoAAtW10fN933Yjy3YO029zt0nwnx/v+zd0weV7PT5gYAAAAAI51wBaCANLW0xS//uCB+9chr0dbe0ed+e04aHR88bu94055jd+r8AAAAAKAYCFcACsS8BWviB796Platb+xzn7GjK+OMv9wr3nbg5HQ5MAAAAABg6AlXAAqgYf0t978cDzy5tM99ykpL4sS37pH2VamsKNup8wMAAACAYiNcAchjz7y6Om789fOxZkNTn/u8aY9d4//+1eyYOqF2p84NAAAAAIqVcAUgDzU0tsZP5r4Uv39qWZ/77FJbkfZVOXL/SVFiCTAAAAAA2GmEKwB55uXF6+O7dzwbqzf03Vvl2EOnxfuOmRU1VW7jAAAAALCz+VYOIE+0tbfHXQ8vjDv+MD86OrLvM2GXqjj7r98U+80Yt7OnBwAAAAC8QbgCkAdWrd8c37vzubRqpS/HHzY93nvsXlFV4dYNAAAAALnkGzqAHHt03vL44a9fiM1NrVnfn7hrVZzzrv1i9h5jd/rcAAAAAIBMwhWAHGlta4+fzn05fvvY4j73OfqgKfHhd+6jWgUAAAAA8ohv6wByYO3GpvjO7c/Ey0uyLwNWXVkef3Pi7Dhy/0k7fW4AAAAAQIGHK2vWrInrr78+7r///liyZElUV1fHXnvtFaeddlp88IMfjLKyskGfe8GCBfH9738/Hn744Vi+fHnU1NTEzJkz413veld67srKym0ev2rVqrjxxhvjgQceSOfW3t4ee+yxR5xwwglxzjnnxOjRowc9N2DkeuG1tfGdXzwbG+qbs76/9/Rd4vxT948Ju1Tv9LkBAAAAANtX0tHR0RF5atGiRXHmmWfGypUrs75/6KGHxpw5c6Kurm7A57777rvj4osvjqampqzvJyFLEursvvvuWd//wx/+EJ/73Odi48aNWd+fNm1a/PCHP+zz+B21cmX26xajceNqo6ysNNra2mPNmvpcTwf6lNxu7/vfRfGz+1+J9iy33pKIOO3omXHKUXtGWWlpTuZYbNw/gMFw7wAGy/0DGCz3D2Cw3D+2mjhxaIsh8vbbu4aGhjj33HPTYGXixIlx1VVXpRUm9957b5x//vlpxcoTTzwRl1xyyYDP/dxzz8VFF12UBit77rln/Ou//ms8+OCDcc8996SBS21tbcyfPz8+8YlPRGtrZoPpF154IT71qU+lwcqkSZPiyiuvjN/97ndx1113pePl5eVpJctnP/vZaGtrG6KfCFDIWlrbYs5dz8VP5r6cNVipqx4Vf/fBQ+LdR88UrAAAAABAnsvbZcFuvvnmWLhwYRpU3HDDDTF79ux0fPz48XHhhRfG5MmT42tf+1oaiDz++ONx2GGH9fvcSZjS0tISY8eOjf/8z/9MA5JOZ599dlp1kgQjr7zySnr+k08+ucfxX/3qV9NgJgl9brrppq7qlOQ8n//859PxZG7z5s2Lhx56KI499tgh+7kAhSdZ/uvfb3u6z/4qMyaPjk+ffqBlwAAAAACgQJTm69I5SS+TxCmnnNIVrHSXLBc2Y8aMdPuWW27p97nr6+vTCpjEe9/73h7BSqekZ0rSfyXx5z//ucd7Tz/9dFoxk/jSl76Uddmv97///elSZRUVFfHMM8/0e27AyLNk5ab4px/9qc9g5S8PmRJf+r+HCVYAAAAAoIDkZeVKUvGxYsWKdPv444/Puk9paWkcd9xxaUP6uXPnpoFMSUnSsWDbkiW/HnnkkbQqJal+6UvnuZLKmd69WhJJdUvvipZOSaiS9GSpqqra7nyAkeuZV1fHtbc/E43NmcsDlpeVxP/9q9nxl4dMzcncAAAAAIARGK50OuCAA/rcb7/99kuf161bF4sXL+538/ikquSQQw7p8/1bb701rXBJHH300RmVK4kjjzwy47ikP0tnGCNYgeL28DPL4gd3Px9t7Zn9VUbXjIrPnnFw7D19l5zMDQAAAAAYgeFK0gw+kQQV26oumTp16198DyRc6S3pv7J27dp49dVX47//+7/jzjvvTMff/e53x1FHHdVj35deeil93nPPPdPnn//85/HTn/40nnvuuWhubk7n9K53vSvOP//8GDNmzKDmAxSupIru1//zWtzywCtZ3582oTY+976DY8KulgEDAAAAgEKVl+FKEnR0VpiUlZX1ud/o0aO7ttevz97PoD9+8YtfxKWXXtpjSbALL7wwzj333B77JeFJUiXTubzYJz7xiXjggQcygqHrr78+XT7shhtuiJkzZ8ZwGDu2pl/LoBWD0tKSrudx42pzPR2KWHt7R/zgrmfjzt/Pz/r+YbN3iy+cdVjUVI3a6XMjO/cPYDDcO4DBcv8ABsv9Axgs948CDFeuvfbauOaaawZ0zOmnnx5XXHFFNDU1pa8rKyu3uX/3pbc6jxmMpUuXZvzleRKMJMt8fepTn+oKMTqXCkt897vfjZUrV6Y9YS644ILYe++9Y82aNXHbbbfFf/zHf6Qhyyc/+cm4/fbbo7p66P9Cvby879CpWCX/TmVlAidyo7WtPa756ZPx4BOLs77/12+bEZ84/aAoKyvd6XNj+9w/gMFw7wAGy/0DGCz3D2Cw3D+KpHJlW9Uqw+H9739/nH322Wkj+qSnShIKPfroo+lzEpj8/d//fbpfY2Nj1zFJsJIsG3bllVd2jSVLmH36059Om91fdNFFsWDBgnTJsI997GNDPufW1jaVK29IUtfkZ5GEYknlAOxsLa1t8c83PR7/8+zrWd8/68TZ8b7j9km329rad/Ls2Bb3D2Aw3DuAwXL/AAbL/QMYLPePrYb6j56HLVw588wz48QTTxzQMZ3LfHVWemyvGqV72LEjDeSnTJnStX3EEUfED37wgzRsSQKWm266Kf0ss2bN6nGNpB/MxRdfnPV8SeiSVL688MILcc899wxLuLJ2bcOQn7NQJeVsSeqa3BzWrNlaXQQ7Q1NLW/zHz5+OZ15dk/FeaUlJ/M1Js+MvD5nqv9k85f4BDIZ7BzBY7h/AYLl/AIPl/rHVxIlb24zkdbgyduzY9DEYnY3gk2W4kkStrwqNjRs39rjeUEmCk89//vPx4Q9/ONrb29O+Kkm4kvRZ6ZQsAzZu3Lg+z/GWt7wlDVdeeSV7U2ug8G1uao1v//dT8fxrW3oxdVdRXhqffM+B8ea9J+RkbgAAAADA8MnLxf9nzJiRPre0tMSKFSv61Sule/XJUDjwwAO7thcv3tJDIVk2bLfddutXP5i6urqM6hpgZAUrV//sz1mDlcqKsvi7DxwiWAEAAACAESovw5V99923a3vevHl97vfcc891VbpMnz69X+d+8skn47zzzkuXLHvttdcGvOTYfvvt1xW4JFU1fVm1alX6PGnSpH7NCygcTc1tcc0tf46Xl6zPeK+msjy+8KE3x+w9hq6aDgAAAADIL3kZruyzzz5pU/jE3Llzs+6TLNd1//33p9tHH310v5u7J9UnDz30UNpsPumH0pdkn04HHHBA1/YxxxyTPq9evTr+9Kc/9Tm3P/7xj+n2m9/85n7NCyicHivX3PrneHFxZrBSVz0qLvrwoTFr6i45mRsAAAAAUMThShKUnHbaaen2bbfd1lWh0t3NN9+cBiSJpPl8f+2///5pv5RE0rh+5cqVWatO/uVf/iXdnjhxYhx33HFd75188sldS3594xvfSPvC9Jacd8mSJen2GWec0e+5AfmtpbUt/v22p7MuBbZLbUX8fx8+NPaYNLSNsQAAAACA/JOX4UoiWborWVIr6buShCe33nprGoQsWrQorr766rjsssvS/ZLlvQ4++OCM4y+66KI46aST0kdvl156aZSWlqbVJx/4wAfijjvuSPu3LF++PG6//fZ4//vfn4YjyT7/8A//EDU1NV3H7rrrrnHxxRen20no86EPfSh+85vfpIHM/Pnz45vf/GZ861vfSt9Prv22t71tGH9KwM7S2tYe//HzZ+LZ+Wsy3htdMyq+eOahMW3iluAVAAAAABjZSjq21Tgkx5Lw4pxzzom1a9dmff/www+P73//+z16onT6yEc+Eo8++mi6/cILL2S8n4QoX/nKV6KpqSnruaurq+PrX/96nHrqqVnfT6571VVXRWtra9b3k6XK/vVf/zVGjx6ev2JfuXLjsJy3EI0bVxtlZaXR1tYea9ZkVhLBjmrv6Igb7nou/vjs8uxLgZ15aEzfTbBSiNw/gMFw7wAGy/0DGCz3D2Cw3D+2mjhxaL+rL488lizhdffdd8ecOXPS3itJdUlSTTJr1qw09DjrrLNi1KhRgzr3e97znjj00EPjhz/8YfzhD39Iz11eXh7Tp09Pg5GPfvSjMXny5D6PT0KfZL8f/ehHaX+VFStWpMuFJUuOvfe9703nV1ZWtgOfHsgHSf7809++nDVYqa3a0rxesAIAAAAAxSWvK1fom8qVraSvDKdf/nFB/PeDr2aMV1eWxRc+dGjMnDImJ/NiaLh/AIPh3gEMlvsHMFjuH8BguX8MX+VK3vZcAci13/15adZgZVR5aXzufYcIVgAAAACgSAlXALJ46pXV8cNfP58xXlpSEp989wGx7+675mReAAAAAEDuCVcAelm0YlN85xfPRLZFEz/617Pj0H0m5mJaAAAAAECeEK4AdLNuU1Ncc+ufo6m5LeO99x87K95x8NSczAsAAAAAyB/CFYA3JIHKNbc+FWs2NGW8d8Lh0+OkI/fIybwAAAAAgPwiXAGIiPaOjvjenc/Gwtc3Zrx3yKzx8aHj94mSkpKczA0AAAAAyC/CFYCIuP2h+fHES6syxvfYrS4+8e4DorRUsAIAAAAAbCFcAYreYy+sjLseXpAxvmtdRfzt+w6OqorynMwLAAAAAMhPwhWgqC1ZVR9zfvlcxnjFqNL43PsOiXFjqnIyLwAAAAAgfwlXgKLV0Nga//7fT6WN7Hs77+T9Y8/Jo3MyLwAAAAAgvwlXgKJtYH/9nc/G8rWbM947+W17xhFv2i0n8wIAAAAA8p9wBShKv/zjwvjzK6szxg/aa3yc/o69cjInAAAAAKAwCFeAovPCa2vj9odezRjfbdfqOP+0/aO0tCQn8wIAAAAACoNwBSgqGxqa47t3PBsdHT3HK0eVxQXvPShqq0blamoAAAAAQIEQrgBF1Wdlzp3PxbpNzRnvffSvZ8f0iXU5mRcAAAAAUFiEK0DR+NUjC+OZ+Wsyxv/ykKnxF/tPzsmcAAAAAIDCI1wBisJLi9fFz383P2N8+sTa+PAJ++RkTgAAAABAYRKuACPe5qbWuP7O59JlwXr3WfnUew6MilFlOZsbAAAAAFB4hCvAiHfzb1+KVesbM8b/5sTZMWV8bU7mBAAAAAAULuEKMKI9/uLK+P1TyzLG337Q5HjbgfqsAAAAAAADJ1wBRqz1m5rixl89nzE+YZeq+PAJ++ZkTgAAAABA4ROuACNSR0dH/OBXz8emzS09xktKIj5+6v5RXVmes7kBAAAAAIVNuAKMSA/+eWk89crqjPF3/cWesc/0XXMyJwAAAABgZBCuACPOmg2N8bO5L2eM7zGpLt599MyczAkAAAAAGDmEK8CIWw7sR/e8EI3NbT3Gy8tK4+OnHpA+AwAAAADsCN8yAiPKI88tz7oc2Bl/uVdMm1CbkzkBAAAAACOLcAUYMTbUN8fNv3kpY3zmlDHxV2/ZPSdzAgAAAABGHuEKMGL8+DcvxqbNLT3GykpL4ux3vSlKS0tyNi8AAAAAYGQRrgAjwhMvroxH563IGD/lqBkxfWJdTuYEAAAAAIxMwhWg4DU2t8Z/3fdixvi0ibVx8tv2zMmcAAAAAICRS7gCFLw7/7Ag1m5s6jFWUhJxzrv2i/IytzkAAAAAYGj51hEoaEtW1ce9/7soY/ydR+yeNrIHAAAAABhqwhWgYHV0dMRN974Qbe0dPcZ3rauIdx89M2fzAgAAAABGNuEKULAeeW55PP/auozxDx2/T1RXludkTgAAAADAyCdcAQpSQ2Nr/HTuyxnjB8wYG2950245mRMAAAAAUByEK0BBuv33r8aG+uYeY+VlJXHWX82OkqSbPQAAAADAMBGuAAVn2er6mPvYkozxk47cIyaPq8nJnAAAAACA4iFcAQrOz+a+HO0dPZvYjx9TFSe/bUbO5gQAAAAAFA/hClBQnl2wJv78yuqM8Q8dv3dUjirLyZwAAAAAgOIiXAEKRnt7R/z0ty9ljO+7+65x2L4TczInAAAAAKD4CFeAgvHQU0tj8cr6HmMlb1StaGIPAAAAAOwswhWgIGxuao2f/+7VjPGjDpwcMyaPycmcAAAAAIDiJFwBCsLdjyyMDQ0tPcYqRpXGGcfMytmcAAAAAIDiJFwB8t7ajU1x7/8uyhj/6yP3jLGjK3MyJwAAAACgeAlXgLx358MLoqW1vcfYrnUVcdJb98jZnAAAAACA4iVcAfLairUN8dCfl2aMn/6OvaKyoiwncwIAAAAAilt55Lk1a9bE9ddfH/fff38sWbIkqqurY6+99orTTjstPvjBD0ZZ2eC/XF2wYEF8//vfj4cffjiWL18eNTU1MXPmzHjXu96VnruyctvLDf3617+OW265JZ599tnYtGlTjBkzJg466KD4wAc+EMcff/yg50X/dXR0xLLV9TFxbE2Ul5bkejoMg9t/Pz/a2jt6jE0ZXxNHHTQ5Z3MCAAAAAIpbSUfy7XSeWrRoUZx55pmxcuXKrO8feuihMWfOnKirqxvwue++++64+OKLo6mpKev7SciShDq77757xnttbW3xxS9+MX75y1/2ef7TTz89vvGNb0Rp6fAUB61cuTGK3abNLXHVT56Mhcs3xqjy0vi7Dx0ab5q+S66nxRBavGJTfPX7j0bvm9Sn33NgHPGm3XI0K0aSceNqo6ysNNra2mPNmvpcTwcoEO4dwGC5fwCD5f4BDJb7x1YTJ46OolgWrKGhIc4999w0WJk4cWJcddVVaYXJvffeG+eff35asfLEE0/EJZdcMuBzP/fcc3HRRRelwcqee+4Z//qv/xoPPvhg3HPPPWngUltbG/Pnz49PfOIT0dramnH8t7/97a5g5Zhjjombb745/vCHP8SPf/zjOProo9Pxn//85/Gd73xnCH4S9OXuRxamwUoi6cfxndueirb2nn05KGy3/e7VjGBlz0mj47DZE3M0IwAAAACAPA5XksBi4cKFUV5eHjfccEOccsopMX78+DQMufDCC+PSSy9N90sCkccff3xA507ClJaWlhg7dmz853/+Z/z1X/91TJ48OWbMmBFnn312XHHFFel+r7zySnr+7pJA5oc//GG6/fa3vz2++93vxmGHHRYTJkyIww8/PL73ve/FEUcckb6fzLu5uXmIfiL0tnRVz6R1Y0NLrFzXmLP5MLReWbI+nnx5Vcb4e4/ZK0pLLAEHAAAAAOROXoYryUplN954Y7qdhCqzZ8/O2CdZLiwJQxJJ35P+qq+vTytgEu9973tj0qRJGfuccMIJaf+VxJ///Oce77388stpVU3ife97X5T0+pI3qahJeq50XivZn+Exqizz17epuS0nc2F4qlZ623f3XeOAmeNyMh8AAAAAgLxuaD9v3rxYsWJFut1XY/ikl8lxxx2XNqSfO3duGsj0DjqySZb8euSRR9KqlKRapS+d50oqZ3pft1O2JcMSo0aNyro/Q6tiVFnGWFOLcGUkeHHRupi3cG3WqpX+/HcOAAAAADCcSvM1XOl0wAEH9Lnffvvtlz6vW7cuFi9e3O/z19XVxSGHHJK1aiVx6623plUnic4eKp2SapnRo7c0vrn99tvTUKe75PVtt92WbifLjs2cObPf82JgKisyw5Vm4cqIcOcf5meMHTxrfOwzfdeczAcAAAAAIO/DlSVLlnRVjWyrumTq1Kld2wMJV3pL+q8klTJJRcsXv/jF+MpXvpKOv/vd746jjjqqx77V1dVxwQUXpNtJE/vPfOYz8eSTT8bq1avjqaeeSt976KGH0r+uv/jii6OysnLQ82LbKkdlWRZMuFLwXlm6Pp5dkFm18p53CCoBAAAAgPyQl8uCrV27tqvCJOlh0pfOCpLE+vXrB329X/ziF3HppZd2vU6CkQsvvDDOPffcrPt/7GMfS5cX+7d/+7f47W9/mz6623vvveOiiy6KY445JobL2LE1Rb880q5jqjPGyivKY9y42pzMh6Fx7e3PZIwdNnu3OGz/KTmZDyNbaWlJ17N7B9Bf7h3AYLl/AIPl/gEMlvtHAYYr1157bVxzzTUDOub000+PK664IpqamtLX26v6qKqq6truPGYwli5dmrG01w033JD2VPnUpz6VEWK0tbVFY2NjV9P73pYtWxaPPvpovPWtb00rXYZDeXnfoVOxqK7M/PVtaW2PsiyN7ikMryxeF396fku/pe7O/KvZ/l0ZVsl9vqysuANrYODcO4DBcv8ABsv9Axgs948iqVzZVrXKcHj/+98fZ599dlRUVMTTTz+dhkJJOJI8r1mzJv7+7/++a98kcPn85z8f9913X7ps2ac//ek444wz0uXLli9fnlbBfOc734k5c+aky4Vdf/31fYYwO6K1ta3oK1cqsiwL1tDYGm1t7TmZDzvuJ/e9kDF28N4TYp/dd/XvyrBI/mojuZcmoXp7e88eWgB9ce8ABsv9Axgs9w9gsNw/thrqP94etnDlzDPPjBNPPHFAx3Qu89VZ7bG9apSkeiRbFctATZmydbmhI444In7wgx+kYUsSsNx0003pZ5k1a1b6/s9//vM0WEl861vfine9611dx06fPj3twXLIIYfExz/+8fjTn/6UnisZG2pr1zZEsWttzuyvsnb95lizpj4n82HHLF65KR555vWM8ZPesrt/U4ZNUg6b/NVG8v+48HsG9Jd7BzBY7h/AYLl/AIPl/rHVxIlb24zkdbgyduzY9DEYY8aMSZ/r6+vTRK2vCo2NGzf2uN5QSSpSkuqUD3/4w9He3h4PPPBAV7jys5/9LH0+9NBDewQr3R199NHxzne+M+655574yU9+MizhChGVFZkVThraF667Hl6QMbbP9F1i9h675mQ+AAAAAAB9ycsmBjNmzEifW1paYsWKzP4L2XqldK8+GQoHHnhg1/bixYu7thcs2PIF8GGHHbbN45N+K4lk/ps2bRrSubFFZZZlwYQrhWnF2ob43yy9Vk59+4yiX/4OAAAAAMg/eRmu7Lvvvl3b8+bN63O/5557rqvSJVmSqz+SPijnnXdeumTZa6+9NuAlx5LAJ9Hc3Nyv6w10X/qvclRm5UpzlqXCyH/3/u+i6Oi15OPMKWPigBnjcjUlAAAAAIDCClf22WefmDZtWro9d+7crPsky3Xdf//9Xctw9fev25Om9Q899FBagZIs29WXZJ9OBxxwQNf2zJkz0+dHHnlkm9dJ+q0kxo0bN6RLlrFVRZZwReVK4dm0uSV+/9SyjPFT3ranqhUAAAAAIC/lZbiSfKF62mmnpdu33XZbV4VKdzfffHPXEl1J8/n+2n///WPvvfdOt5Nm8ytXrszYZ9WqVfEv//Iv6fbEiRPjuOOO63qvs8/KSy+9FP/1X/+V9RpJ8NIZ3Jx88sm+IB4mVVl7rrTnZC4M3v2PL47m1p7/bpPG1cQh+0zI2ZwAAAAAAAouXEkkS3dNmjQpXYYrCU9uvfXWNAhZtGhRXH311XHZZZel+yXLex188MEZx1900UVx0kknpY/eLr300igtLY3Vq1fHBz7wgbjjjjvS/i3Lly+P22+/Pd7//vfHkiVL0n3+4R/+IWpqarqO/chHPtIVznz961+PL3/5y/HUU0/FunXrYv78+XHttdfG+eefn1bWJH1gPv3pTw/rz6mYZVsWTOVKYWlpbYvfPra1p1GnE9+6e5QKJQEAAACAPFUeeaquri6uu+66OOecc2Lt2rVpINLb4YcfHldeeWXW45ctW5aGHdkcddRRcfnll8dXvvKVNFT54he/mLFPdXV1Gp6ccMIJPcaT/itz5syJz3zmM/Hss8/Gz372s/TR24wZM9KgJVkWjOFhWbDC98dnl8eGhi19jDqNrhkVRx0wOWdzAgAAAAAo2HClcwmvu+++Ow0zkt4rSRCSVJPMmjUrTj311DjrrLNi1KhRgzr3e97znjj00EPjhz/8YfzhD39Iz11eXh7Tp09Pe7h89KMfjcmTs3/Bm1Sk/PSnP02rXH71q1+ly5Zt3Lgxamtr034xSTVNUv2SBDTs5Ib2wpWC0d7REfc8+lrG+PGHTc8anAEAAAAA5IuSjo6OjlxPgoFbuXJjFLvkV/fjVz6QfknfadyYyvjnT789p/Oif558eVX8261P9RgbVV4a//zpo2J0TUXO5kVxGTeuNsrKSqOtrT3WrKnP9XSAAuHeAQyW+wcwWO4fwGC5f2w1ceLoKIqeK7A9JSUlUVnR81e4qVnlSqG4N0vVytEHTRGsAAAAAAB5T7hCQeu9fFRTS3vO5kL/LXx9Yzz/2roeY0n7+r96y+45mxMAAAAAQH8JVxhRfVda29qjvd1Kd/nut48vzhg7dN+JMWlcTU7mAwAAAAAwEMIVRlxT+yZN7fPaps0t8T/PLc8Yf+cR03MyHwAAAACAgRKuUNCEK4Xn908ti5bWnsu3TZ9YG/vuvmvO5gQAAAAAMBDCFQpa5ajMX2HhSv5Klmy7/4nMJcGOO3x6lJQkXVcAAAAAAPKfcIUR1dA+0dQsXMlXT7+6Olaua+wxVl1ZHm/bf3LO5gQAAAAAMFDCFQpaZUVmuNLc0nPJKfLH3MeXZIy9/aDJWf8dAQAAAADylXCFgqbnSuFYvrYhrVzp7bjDNLIHAAAAAAqLcIWCJlwpHPdnqVo5YOa4mDyuJifzAQAAAAAYLOEKBU3PlcKQBF6/f2pZxvjxqlYAAAAAgAIkXKGgVY7K/BVWuZJ//nfeimhoau0xNn5MVRw8a3zO5gQAAAAAMFjCFQqaZcEKw++eWpox9n8OmxalpSU5mQ8AAAAAwI4QrlDQhCv5b9nq+nh58foeY2WlJXH0QVNyNicAAAAAgB0hXKGgVVYIV/LdQ1l6rbx57wkxprYiJ/MBAAAAANhRwhVGXEP75ub2nMyFTK1t7fHw05nhyjsOUbUCAAAAABQu4QoFzbJg+e3PL6+ODQ0tPcbGjq6MA2dqZA8AAAAAFC7hCgWtyrJgee2hLI3s337QFI3sAQAAAICCJlxhxC0LJlzJD2s3NsXTr67OGD/6YEuCAQAAAACFTbhCQasclfkr3CxcyQu/f3pZdHT0HNtvz7Gx267VuZoSAAAAAMCQEK5Q0PRcyU/tHR3x0J8zlwTTyB4AAAAAGAmEK4zAcKU9J3NhqxdeWxer1jf2GKutKo/D952YszkBAAAAAAwV4QoFbVR5aZT06o3e1KxyJdf++MzrGWN/ccDkGFWeGYYBAAAAABQa4QoFraSkJKN6xbJguZX0vPnTCysyxo8+yJJgAAAAAMDIIFyh4FVVlPd4raF9bj358qpo7FU9NHVCbewxqS5ncwIAAAAAGErCFQpeZUXPypXm1va0oTq58cizyzPG3nbApLTKCAAAAABgJBCuUPCqeoUrCdUrubGxoTmefnV1xviR+0/KyXwAAAAAAIaDcIURtyxYoqmlPSdzKXZ/en5FtLX3rBrad/ddY8Iu1TmbEwAAAADAUBOuMOKWBUtoap8bf+xjSTAAAAAAgJFEuMLIXBasV0N1ht+KdZvj5SXre4yVl5XEEW/aLWdzAgAAAAAYDsIVCl5l1mXBhCs72yPPvp4xdvCsCVFbNSon8wEAAAAAGC7CFUZk5UqjcGWn6ujosCQYAAAAAFA0hCuMyJ4rlgXbuRa8vjGWr2noMVZTWR4HzxqfszkBAAAAAAwX4QojsnLFsmA71/88l1m1kvRaGVWe+W8DAAAAAFDohCsUPD1Xcr8k2GMvrMgY/4v9LQkGAAAAAIxMwhVGaOVKe07mUozmL9sYqzc09RjbpbYi9t1915zNCQAAAABgOAlXKHhVoywLlkt/ej6zauWw2ROjtLQkJ/MBAAAAABhuwhVG5LJgzcKVnbYk2P9mCVfeMnu3nMwHAAAAAGBnEK4wMpcFaxau7AwLXk+WBGvsMTamZpQlwQAAAACAEU24QsGrzNpzRbiSuyXBdrMkGAAAAAAwoglXKHjVlZnLgglXcrkk2MSczAcAAAAAYGcRrjAiK1eaW9pzMpdisnD5xli1vueSYKOTJcH2sCQYAAAAADCyCVcoeFVZGtqrXBl+f3p+ZcbY4ftOjLJStxUAAAAAYGTzLSgFT8+V3CwJlq3fyuFv2i0n8wEAAAAA2JmEKxS8KuHKTvfa8k2xYt3mHmN11aPiTZYEAwAAAACKgHCFgldRXhYlJT3HmpqFK8PpsRczq1YOsyQYAAAAAFAkMptV5Jk1a9bE9ddfH/fff38sWbIkqqurY6+99orTTjstPvjBD0ZZWWbVwo64+uqr47rrrotp06bF3Llzt7nvn/70p7jxxhvj8ccfjw0bNsS4cePi8MMPj7/5m7+JQw89dEjnRd9KS0vS6pXNTVsDlUbhyrB68qVVGWNHvGliTuYCAAAAALCz5XW4smjRojjzzDNj5cqtjbObm5vjiSeeSB933HFHzJkzJ+rq6obkeo899lga5PTHTTfdFF//+tfT3hOdli9fHnfffXf8+te/ji984Qtx7rnnDsm86F9T++7himXBhs/KdZtj8cr6HmPVleXxpj3G5mxOAAAAAAA7U96u4dPQ0JCGE0mwMnHixLjqqqvi4YcfjnvvvTfOP//8tGIlCVguueSSIbnepk2b4qKLLoq2tu1/Kf/ggw/GP/3TP6XByjve8Y645ZZb4pFHHkkDlyOOOCLa29vjW9/6Vlptw85RVdkzJ2xpbY+29vaczWcke/LlzKqVg/YaF+VleXs7AQAAAAAYUnn7bejNN98cCxcujPLy8rjhhhvilFNOifHjx8eee+4ZF154YVx66aXpfvfcc0+6LNeOuuyyy2Lx4sXb3S8JVP75n/85DVAOO+ywdAmxgw8+OMaOHZsGKz/4wQ/SJcGS/b75zW+m+zH8qisyi7Camv3sd9aSYG/eZ0JO5gIAAAAAkAt5Ga4kwUTSyySRhCqzZ8/O2CdZLmzGjBnpdlI5siPuu+++uO2229Lw5phjjtnmvr///e/jxRdfTLc/97nPpeFPdxUVFfHFL34x3Z4/f37al4XhV1WZ2XvH0mBDr6GxJV5ctK7HWFlpSRy01/iczQkAAAAAYGfLy3Bl3rx5sWLFinT7+OOPz7pPaWlpHHfccel20ni+e++TgUiWHfvyl7+cbn/ta19Lm9Jvb0mwxJgxY+Itb3lL1n2SipakkiXxm9/8ZlDzYmCSnh+9NTa35mQuI9lTr66Otvae/63tu/uuUVs1KmdzAgAAAADY2fI2XOl0wAEH9Lnffvvtlz6vW7euX0t6ZZMsL7Z27do444wz4oQTTtju/s8//3z6/KY3vSnt+5JNSUlJ19yeffbZQc2LHeu5kmhsVrky1CwJBgAAAACQp+HKkiVL0udkya3Jkyf3ud/UqVO7tgcTrvz4xz9OK1GmTZvW1cOlv3ObPn36NvfrnNtgQx+GoueKcGUotba1x9OvrskYf/PewhUAAAAAoLhkfiOdB5JKkkRdXV2f1SGJ0aNHd22vX79+QNdI+qFceeWVaZXJ5Zdfnl5rIHPbZZddtrlf59w2bNgQw2Hs2Jp07iRLxJVk7bkyqnJUjBtXm5M5jUR/fmllbG7qudTanpNHx+y9hCsU9v2j89n9Augv9w5gsNw/gMFy/wAGy/2jAMOVa6+9Nq655poBHXP66afHFVdcEU1NTenrysrKbe5fVVXVtd15TH+0trbGRRddFJs3b46PfvSjceSRR/b72P7OrfP9gcxrIMrL+w6dilG2nitJQ/uysrwszipIf3p+Sx+k7o48cIqfMSNCElaXlQmsgYFx7wAGy/0DGCz3D2Cw3D+KpHJlW9UqQxX8PPXUUzFr1qy48MILBzy39vb2yLXW1jaVK29IUtds4UpDY0u0teX+32ok6OjoiP95ZlnG+BFv2s3PmIK/fyT30uR3vL29I9fTAQqEewcwWO4fwGC5fwCD5f6x1VD/kfiwhStnnnlmnHjiiQM6pnMprerq6n5VfTQ2NmatYtmWJ598Mq677rq0n0uyLNj2KlB6S+bW0tISzc3NQ1LhMlhr1zYMy3kLUVLOVpWl58qatQ2xZk19TuY00ixesSlWrN3cY2yX2ooYVzvKz5iCv38kf7WR/D8u/C4D/eXeAQyW+wcwWO4fwGC5f2w1ceLWNiN5Ha6MHTs2fQzGmDFj0uf6+vo0UeurQmPjxo09rrc9DQ0N6XJgbW1t8dnPfjYOPPDAAc8tCYCSPirdr51NZ6+Vwf4MGJjqLD1XGls0tB8qT7y8KmPskL0nRKnqKQAAAACgCOXlsmAzZsxIn5MKkRUrVsSkSZOy7rd06dKu7SlTpmz3vE8//XQsXLgw3f72t7+dPvqyZMmSmD17drp9wQUXpGFMYubMmel73a+dzbJlW5ZQmjp16nbnxY6rrhyVMdbYLFwZKk+/sjpj7M37aGQPAAAAABSnvOxEve+++3Ztz5s3r8/9nnvuua5Kl+nTp+/UuT3//PNpVU02yXjnvPfbb7+dMq9iV5WlcqVJuDIk6htb4pWl63uMjSovjf33VJUFAAAAABSnvKxc2WeffWLatGlphcjcuXPj2GOPzdgnaSp///33p9tHH310v5q7H3HEEfH4449vc5+vfvWrceedd6YVJ3fddVc6NmrU1qqIv/zLv4zvf//7sXr16rR/y6GHHppxjuQaa9euTbff8Y539OMTs6Oy9VxRuTI05i1YG71zxNm77xoVozIDLQAAAACAYpCXlStJUHLaaael27fddltXhUp3N998cyxYsCDdPvvss/t13rKysqitrd3mI2l03zmHzrGKioqucxx55JFp8JO48sorMxrbJ6//+Z//uSskEq7sHNWVmeFKk54rQ+LpVzOXBDtwr/E5mQsAAAAAQD7Iy3Alcd5556W9VpK+K0l4cuutt8bKlStj0aJFcfXVV8dll12W7nfiiSfGwQcfnHF80rj+pJNOSh9DqbS0NL70pS91Vaicc8458dhjj6WVKslz8joZT8KZ//f//l+/KmoYnnClsbk1J3MZSZIl7p6ZvyZj/KC9xuVkPgAAAAAA+SAvlwVL1NXVxXXXXZeGFUlwcemll2bsc/jhh6fVI301lJ8/f/6wzO2d73xn/O3f/m3827/9W/zv//5vfPjDH+7xfhKoXHLJJXHccccNy/XJpOfK8Fiyqj7WbmzqMTZ+TFVMHleTszkBAAAAAORa3oYrif333z/uvvvumDNnTtp7ZenSpWnlyKxZs+LUU0+Ns846q0c/lJ3pM5/5TLpE2I9+9KO0YmXdunUxZsyYtAfLxz72sXjrW9+ak3kVq+psPVcsC7bDnnk1e9WKiiwAAAAAoJiVdCTr/lBwVq7cmOsp5I1x42qjtLQk3v3FO3o0Xp+wS1Vc+amjcjm1gvetm5+IeQvX9hj7zOkHxeGzJ+ZsTjDU94+ystJoa2uPNWvqcz0doEC4dwCD5f4BDJb7BzBY7h9bTZw4Ooqi5woMRFJJUdWreqXRsmA7JOlZ89LidT3GykpLYr89x+ZsTgAAAAAA+UC4wohRVdGz74pwZcc8/9q6aG3rWdg2a9ouUVOV16sJAgAAAAAMO+EKI0Z1Zc8v/Vvb2tMHg/PMq6uz9lsBAAAAACh2whVGbOVKollT+yFtZn/gzPE5mQsAAAAAQD4RrjBiK1cSlgYbnOVrG2LFus09xsbUVsTuk+pyNicAAAAAgHwhXGHEqBKuDGvVygEzxkVpSUlO5gMAAAAAkE+EK4wYVRWZ4UqTZcEG5dn5meGKfisAAAAAAFsIVxgxqioze66oXBm4tvb2eP61tRnj+88UrgAAAAAAJIQrjPCeK605mUshW/D6xoxQao/d6mJMTUXO5gQAAAAAkE+EK4wY1dmWBVO5MmDPL8ysWnnTnmNzMhcAAAAAgHwkXGHEyLosmJ4rAzYvS7iyn3AFAAAAAKCLcIWR3dBe5cqAtLS2x0uL1/cYKy0piX133zVncwIAAAAAyDfCFUZ4zxXhykC8unR9GrB0N3PK6Kw/WwAAAACAYiVcYUQvC6ZyZceXBNNvBQAAAACgJ+EKI7qhvZ4rA6PfCgAAAADA9glXGDGqsixd1dTcmpO5FKKkyufVpRt6jJWXlcTe03bJ2ZwAAAAAAPKRcIURo6oic1kwPVf676XF66KtvaPHWBKsVIzK/LkCAAAAABQz4Qojhob2O0a/FQAAAACA/hGuMLKXBdNzpd/0WwEAAAAA6B/hCiNGdZZlwZI+ImxffWNLLFy+scdY5aiymDllTM7mBAAAAACQr4QrjBhJb5CSkp5jjRra98uLr62Ljp7tVmKf3XeJ8jK3CAAAAACA3nxzyohRUlKS0dRez5X+ec6SYAAAAAAA/SZcYURJlrLqTs+V/nnhNeEKAAAAAEB/CVcYUSoreja1b23riNa29pzNp1D6rSxZWd9jrLqyPPbYbXTO5gQAAAAAkM+EK4woVb0qVxKWBtu2lxavj17tVmKf6btEaWmvBjYAAAAAAKSEK4wovXuuJJqEK9v00qJ1GWNJuAIAAAAAQHbCFUaUyizhSqO+K9utXOlt3913zclcAAAAAAAKgXCFEUXlysA0t7TF/GUbeoyVl5XGjMljcjYnAAAAAIB8J1xhRKnM2nOlNSdzKQRJsNLW3rPjyl5TRseocrcGAAAAAIC++AaVEaWqojxjTOVK317MsiTYPpYEAwAAAADYJuEKI4qeKzvezF6/FQAAAACAbROuMKLoudJ/7e0d8fKSnpUrJSURe0/bJWdzAgAAAAAoBMIViqDninAlm0UrNmX8bHbfrS6qKzOXVgMAAAAAYCvhCiO+ckVD++xeXJy5JNg+0y0JBgAAAACwPcIViiBcUbmSjX4rAAAAAACDI1xhxDe0b9LQPkNHR0e8uLhnv5XEvtP1WwEAAAAA2B7hCiNKdUVmv5DNTZYF623Fus2xob65x9huY6tjl7rKnM0JAAAAAKBQCFcYUSwL1j8vZlsSTL8VAAAAAIB+Ea4wolRXZlauNKpcyfDSoswlwfaxJBgAAAAAQL8IVxhRVK70z0uLNbMHAAAAABgs4QojSlW2nivNKle627S5JZav3dxjbEzNqLTnCgAAAAAA2ydcYUQpLS2JylE9q1dUrvT06tLMJcFmTdslSkpKcjIfAAAAAIBCI1xhxC8NtrlJuNLdK0s2ZIztNXVMTuYCAAAAAFCIhCuMOFW9mtq3trWnD7ZRuTJVM3sAAAAAgP4SrjDiaGrft/aOjnh12cYeY8lqYDOmjM7ZnAAAAAAACo1whRGnOku4srlJU/vE66sbMn4W0yfWRVVFz2ofAAAAAAD6lvffqK5Zsyauv/76uP/++2PJkiVRXV0de+21V5x22mnxwQ9+MMrKMr9I3xFXX311XHfddTFt2rSYO3dun/u1t7fHr371q/jFL34Rzz77bKxfv75rbieccEKceeaZUVdXN6Rzo3+yBQUqV7Z4JcuSYPqtAAAAAACMoHBl0aJFaUixcuXKrrHm5uZ44okn0scdd9wRc+bMGbIQ47HHHkuDnO2pr6+PCy64IB5++OEe4y0tLfHkk0+mj5/97Gfxve99L2bOnDkkc6P/qitVrvTl1aWa2QMAAAAAjNhlwRoaGuLcc89Ng5WJEyfGVVddlYYZ9957b5x//vlpxUoSsFxyySVDcr1NmzbFRRddFG1t269w+NKXvtQVrLzvfe+L2267LR555JH4+c9/Hh//+MejvLw8XnvttXQ7+RzsXCpX+vbKksxwRTN7AAAAAIARUrly8803x8KFC9Og4oYbbojZs2en4+PHj48LL7wwJk+eHF/72tfinnvuiccffzwOO+ywHbreZZddFosXL97ufk899VR6zcQnP/nJ+Lu/+7uu98aOHRv7779/vPnNb47PfOYzaeVN8jmSkIidpypL5Upjs8qVpHpnyapNPcaqK8tj8vianM0JAAAAAKAQ5WXlSkdHR9x4443p9imnnNIVrHSXLBc2Y8aMdPuWW27Zoevdd999afVJEtwcc8wx29z317/+dfpcU1OThivZJD1XDjrooHT7gQce2KG5MXAqV7Jb8PrG6OjIXBKstKQkV1MCAAAAAChIeRmuzJs3L1asWJFuH3/88Vn3KS0tjeOOOy7dThrPJ4HMYCTLjn35y19Ot5NKmHHjxm1z/1WrVsWoUaNin332SRvY92XPPfdMnzs/BztPdYWeK9m8mqWZ/Sz9VgAAAAAARk640umAAw7oc7/99tsvfV63bl2/lvTK5tJLL421a9fGGWeckVacbM+VV14ZTz/9dHz/+9/f5n7JkmaJXXbRz2JnU7mSnWb2AAAAAAAjOFxZsmRJ+pz0W0l6q/Rl6tSpXduDCVd+/OMfx4MPPhjTpk1LQ5b+Kikpibq6uj7ff+aZZ9IAJnH44YcPeF7smOosPVeKvXIlqex6JWu4IvwDAAAAABgRDe2TSpJEEmCUlWV+Ud5p9OjRXdvr12cuebQt8+fPT6tQkqDk8ssv32ZYMhBNTU3xla98pSsc+uAHPxjDYezYmnTuJEvElXQ9jxtXG7tNyPy37CjZ8l6xWr6mITbUN/cYmzqhNvaYtmvO5gT5eP8A6A/3DmCw3D+AwXL/AAbL/aMAw5Vrr702rrnmmgEdc/rpp8cVV1yRBhSJysrKbe5fVVXVtd15TH+0trbGRRddFJs3b46PfvSjceSRR8ZQaGtriy9+8Yvx7LPPpq/PO++8mDFjRgyH8vK+Q6dilYRNZWUlUVs9KuuyYGVleVmotVO8vHhdxtjsPccW9c8Est0/AAbCvQMYLPcPYLDcP4DBcv8oksqVbVWrDFXw89RTT8WsWbPiwgsvHJJzNjc3p8HKPffck75++9vfHn/7t38bw6W1tU3lyhuS1DX5WSRLX7W3d0TlqMzfn/rNLdHW1h7Fat6CNRlj++w+tqh/JpDt/gHQH+4dwGC5fwCD5f4BDJb7x1ZD/YfmwxaunHnmmXHiiScO6JjOZb6qq6v7VY3S2NiYtYplW5588sm47rrr0iW7kmXBtlcd0x+bNm2Kz372s/Hwww+nr4844oj49re/Pawh0dq1DcN27kKTlLMlqWtyc1izpj6aNvdc/iqxsb4pfa9YPffq6oyxKbtWFfXPBLLdPwD6w70DGCz3D2Cw3D+AwXL/2GrixK1tRvI6XBk7dmz6GIwxY8akz/X19Wmi1leFxsaNG3tcb3saGhrS5cCS5buSMOTAAw+MHbV48eL45Cc/GS+99FL6+h3veEcarHQGROx81ZWZv9abm9qiWLW2tcdry7f+t5KoKC+NaROtsQgAAAAAMGKWBevsU9LS0hIrVqyISZMmZd1v6dKlXdtTpkzZ7nmffvrpWLhwYbqdBCDJoy9LliyJ2bNnp9sXXHBBGsZkO18SrKxatSp9fcYZZ8TXvva1GDUqs+cHO09lRWbFUGNzaxSrJSvro7WtZ8nfHpNGR7l+KwAAAAAAg5KX367uu+++Xdvz5s3rc7/nnnuuq9Jl+vTpsTP9z//8T3zkIx/pClaS8OXyyy8XrOSB0pKSjIAlaWhfrBa8viFjbMbkoS2BAwAAAAAoJnlZubLPPvvEtGnT0uqRuXPnxrHHHpuxT3t7e9x///3p9tFHH92v5u5JL5THH398m/t89atfjTvvvDOmTp0ad911VzrWOzB56qmn0oqVzZs3p71bvv71r6dVK+SPqoqyaOoWqBRz5cqC13suCZaYMUW4AgAAAAAwoipXkqDktNNOS7dvu+22rgqV7m6++eZYsGBBun322Wf367xJg/na2tptPpKwpHMOnWMVFRVd59iwYUN87nOfS/u3lJaWxtVXXy1YyUPVFT1zw2RZrJbW9ihG2cKVPSdv6WsEAAAAAMAIqVxJnHfeeWmwsnz58jQ8+eIXvxjHHHNMNDY2xq233hrXX399ut+JJ54YBx98cMbxSeP6pMIk8etf/3rI5vWd73ynq9fLxz72sXj7298e9fX1fe6fBDCa2+emcqW3pHplVPnWoKwYJIHS4hWbeoxVjiqLKeNqcjYnAAAAAIBCl7fhSl1dXVx33XVxzjnnxNq1a+PSSy/N2Ofwww+PK6+8Muvxy5Yti/nz5w/pnJqamuInP/lJ1+vvf//76WNbkuXNkqXN2LmqKzN/tTc3t8XoIssUlqzaFG3tvZvZ10Vp6faX0QMAAAAAoMDClcT+++8fd999d8yZMycNKJKKkaQSZNasWXHqqafGWWedtVMbyL/44ovpcmAUaOVKU/H1XVmwLEu/FUuCAQAAAADskJKOjo6ef9ZOQVi5MvNL82I1blxtlJWVRltbe6xZs2WJtuvvfC7++OzrPfa7+KzDYt/dd41icuOvno/f/XnLMnadPn7K/vG2AyfnbE6Q7/cPgO1x7wAGy/0DGCz3D2Cw3D+2mjhxdIz4hvawo6orMytXNhdj5crrGzLGZkwZ2psIAAAAAECxEa4wIlVVZK5419jcFsWkpbUtlqzsmUZXVpTFJM3sAQAAAAB2iHCF4qlcaS6uypXFK+szmtnvOWl0lJZoZg8AAAAAsCOEKxRP5UpTcVWuLHg9WzN7S4IBAAAAAOwo4QojUlVFZuVKY5FVrixYlqXfinAFAAAAAGCHCVcYkfRciViYpXJlT+EKAAAAAMAOE65QPD1XmlqLq5n9qvqMah7N7AEAAAAAdpxwhRGp2CtXFq3QzB4AAAAAYLgIVyieypUi6rmy4PUs/VamWBIMAAAAAGAoCFcYkYq9cmWBfisAAAAAAMNGuMKIlPQX6a2xiHquLFiWGa7MnDwmJ3MBAAAAABhphCuMSJVZwpXNTcVRudLc0hZLezWzT5ZJmzi2OmdzAgAAAAAYSYQrjEhJ4/be1SuNRdJzZcmq+mjv6NnMfo/dNLMHAAAAABgqwhVGrOrK8oyeKx29QoeRaNGKTRlje0zSbwUAAAAAYKgIVxixeleutLV3RGtbe4x0i5ZnC1fqcjIXAAAAAICRSLjCiFVV0bNypVj6rry2IrOZ/e67CVcAAAAAAIaKcIWiqVwphr4rSa+V3suClZWWxNQJtTmbEwAAAADASCNcoWh6rhRD5cqq9Y1pb5nupoyvjfIy/6kDAAAAAAwV37gyYhVj5cqi5ZlLgum3AgAAAAAwtIQrjFjVRdhzpfeSYIk99FsBAAAAABhSwhVGrKrKzMqVzSO8cuW15Znhimb2AAAAAABDS7jCiFWTtedKa9FVruw+aXRO5gIAAAAAMFIJVyiyhvYjN1ypb2yJ1Rsae4yNG1MZddWjcjYnAAAAAICRSLhCUYUrDSM4XFmUbUmwiZYEAwAAAAAYasIViqxyZeQ2tLckGAAAAADAziFcYcQqtp4rr63YmDG2h2b2AAAAAABDTrjCiFVdWVZU4Ur2yhXhCgAAAADAUBOuMGIVU8+V1rb2WLqqvsdYZUVZTNy1OmdzAgAAAAAYqYQrFFnPlZEZrixb3RCtbR0ZzexLS0pyNicAAAAAgJFKuMKIVVVRFr2zhZEarizK0m/FkmAAAAAAAMNDuMKIVVJSEtUV5UURrry2PLPfimb2AAAAAADDQ7hCUS0N1tjUFu0dPZfPGrHN7HcbnZO5AAAAAACMdMIViipcSWKVpua2GEk6OjoywpVkObRpE2tzNicAAAAAgJFMuMKIVlNZljE20pYGW7epOTZtbukxNnlcTVSOyvzsAAAAAADsOOEKRVW5kmgYYeHK4pXZlgTTbwUAAAAAYLgIVyi6cGWkVa4sWVmfMTZtonAFAAAAAGC4CFcY0YohXMlWuTJ9gn4rAAAAAADDRbjCiFYMy4Jlr1wRrgAAAAAADBfhCiNaddaG9m0xUrS3d8TS1T3DlYpRpTFh1+qczQkAAAAAYKQTrjCi1YzwZcFWrNscLa3tPcamTaiN0pKSnM0JAAAAAGCkE64woo30nitLsvRb0cweAAAAAGB4CVcY0UZ6z5Vs/VY0swcAAAAAGF7CFUa0kV65sljlCgAAAADATidcofh6rjSOnHBlyaoslSsTVa4AAAAAAAwn4Qoj2kiuXGlpbYvlazb3GKurHhVjaityNicAAAAAgGIgXKEIe660xUiwbHVDtHd09BibNqE2SkpKcjYnAAAAAIBikPfhypo1a+Kb3/xmnHTSSXHQQQfFW9/61vjQhz4UP/7xj6Otbei/JL/66qtj9uzZcdxxxw342BUrVsSRRx6ZHn/bbbcN+dwYuKrKsugdNTQ2t47cZvb6rQAAAAAADLvMP+vPI4sWLYozzzwzVq5c2TXW3NwcTzzxRPq44447Ys6cOVFXNzRfKD/22GNx/fXXD/r4Sy65JNatWzckc2FolJaUpAHL5m7VKiNlWbDFq7I1s9dvBQAAAACgaCtXGhoa4txzz02DlYkTJ8ZVV10VDz/8cNx7771x/vnnR1lZWRqwJIHGUNi0aVNcdNFFg66Guemmm+Khhx4akrkwvEuDJUFLR6/ltAqRyhUAAAAAgNzI23Dl5ptvjoULF0Z5eXnccMMNccopp8T48eNjzz33jAsvvDAuvfTSdL977rknHn/88R2+3mWXXRaLFy8e1LGvvPJKXHnllTs8B3ZOuJL0KWlqKfy+K0tWZlauTJ2gcgUAAAAAoCjDlaSq4MYbb0y3k1Al6WHSW7Jc2IwZM9LtW265ZYeud99996U9UpLw5phjjhnQsa2trWnFS2NjY5xxxhk7NA92XlP77suEFaJkabPVG5p6jI0bUxk1VXm90h8AAAAAwIiQl+HKvHnz0ubwieOPPz7rPqWlpV1N5+fOnTvoZZ6SZce+/OUvp9tf+9rXYty4cQM6/t///d/jmWeeiYMOOig++clPDmoODK+aLOFKQ4H3XbEkGAAAAABA7uRtuNLpgAMO6HO//fbbL31OmsgPdkmvZHmxtWvXplUnJ5xwwoCOTXq+fO9734uqqqr45je/mfaBoVAqV1pHXjN7S4IBAAAAABRvuLJkyZL0Oem3Mnny5D73mzp1atf2YMKVH//4x/Hggw/GtGnTunq49Fd9fX26HFhbW1v8v//3/2LWrFkDvj47R3VF2YgLV7JVrkybKFwBAAAAANgZ8rJBQ1JJkqirq9tmNcjo0aO7ttevXz+ga8yfPz9tQl9SUhKXX355eq2B+MY3vhGvvfZa/MVf/EX8zd/8TexsY8fWpHMnWSKupOt53LjMgGHsrtUZY2XlZVn3LRTL127OGNt/74kF/ZkgH+8fANm4dwCD5f4BDJb7BzBY7h8FGK5ce+21cc011wzomNNPPz2uuOKKaGra0qi7srJym/sny3F16jxmIE3oN2/eHB/96EfjyCOPHNA8f/vb38att96ahjtJMJOLkKO83BJkvSX/DmVlmf8WddUVGWObm9uirCwvC7e2K+kvtPD1jT3GknvknpPHFOxngny9fwBsi3sHMFjuH8BguX8Ag+X+USSVK8PduyQJfp566ql0Ka8LL7xwQMeuWrUq/v7v/z7dTpYS67402c7U2tqmcuUNSeqa/CyS0KG9vSPj/erKzN+nTQ3N0dbWHoVo7cbG2NjQ3GNsyoTaKCstKdjPBPl6/wDIxr0DGCz3D2Cw3D+AwXL/2Gqo/zB92MKVM888M0488cQBHdO5zFd1dXW/qlEaGxuzVrFsy5NPPhnXXXdd2s8lWRZse9UxvSXBypo1a+KEE05IK21yZe3ahpxdO98k5WxJ6prcHNasyexF0tGaGTisXteQdd9CMG/BmoyxyeNqCvbzQD7fPwCyce8ABsv9Axgs9w9gsNw/tpo4cWubkbwOV8aOHZs+BmPMmDFdTeOTRK2vCo2NG7cujdSfazU0NHQ1of/sZz8bBx544IDm9ZOf/CTuv//+GDduXHz9618f0LHkTnVl5q/55sa2KFRLV2cGa9MmWC8RAAAAAKColwWbMWNG+tzS0hIrVqyISZMmZd1v6dKlXdtTpkzZ7nmffvrpWLhwYbr97W9/O330ZcmSJTF79ux0+4ILLkjDmF/+8pfp66Ry5W1ve9s2r/WlL30pfSReeOGF7c6N4ZNtWbCGptYoVEtXZSbMU4UrAAAAAAA7TV52v9533327tufNm9fnfs8991xXpcv06dN3ytwYIZUrIy1cGS9cAQAAAAAo6sqVffbZJ6ZNm5ZWj8ydOzeOPfbYjH3a29vTJboSRx99dL+aux9xxBHx+OOPb3Ofr371q3HnnXemjervuuuudGzUqFHp8/XXX58uKdaXZcuWxcknn5xu/+M//mOceuqp250Tw68mS7jS2Fy44cqy1T3DleRXf9K4mpzNBwAAAACg2ORl5UoSlJx22mnp9m233dZVodLdzTffHAsWLEi3zz777H6dt6ysLGpra7f5SBrdd86hc6yioiIdq6qq2uaxyfudkmM6x8mt6qryEbMs2MaG5tjQ0NJjbLddq2NUeV7+pwwAAAAAMCLl7Tey5513XtprJem7koQnt956a6xcuTIWLVoUV199dVx22WXpfieeeGIcfPDBGccnjetPOumk9EFxq64YOcuCLcvSzF6/FQAAAACAnSsvlwVL1NXVxXXXXRfnnHNOrF27Ni699NKMfQ4//PC48sor+1yia/78+TthpuS70tKSqKwoi6bmrUu6bW7qe3m3fKaZPQAAAABA7uVtuJLYf//94+677445c+akvVeWLl0apaWlMWvWrLSfyVlnndXVDwW213elZ7jSGh0dHf3q1ZNPlvbqt5KYMl6/FQAAAACAnamkI/mGmYKzcuXGXE8hb4wbVxtlZaXR1tYea9Zkhg+JL8/5n1jSq+rjO//vmLSipZBc9ZMn4tkFa3uMfeVjR8SMyWNyNicY6fcPgN7cO4DBcv8ABsv9Axgs94+tJk4cHUXRcwWGu6l9fWPPxvCFYGmWnitTxlkWDAAAAABgZxKuUBRqKzPDlYYCa2qfLGW2dmNTj7EJu1QVXPUNAAAAAEChE65QFGqyVK40NLaOgH4rqlYAAAAAAHY24QpFoaZqVMEvC7a0V8+YxNQJmtkDAAAAAOxswhWKQu0IqFxZtiqz38pUlSsAAAAAADudcIWiUFM5MpcFmzpBuAIAAAAAsLMJVygKI3VZMD1XAAAAAAB2PuEKxbssWFPhVK40NbfF6vWNPcZ2rauImiyfCwAAAACA4SVcoShkCyEKaVmw19c0REevMUuCAQAAAADkhnCFol0WrJDClWz9ViwJBgAAAACQG8IVirihfUtB91tRuQIAAAAAkBvCFYp2WbD6Auq5kjVcGV+Tk7kAAAAAABQ74QpFoaqiLEpLSgp4WbCGjDGVKwAAAAAAuSFcoSiUlJRkVK8USrjS0toeK9du7jFWVz0qRtdU5GxOAAAAAADFTLhC0egdrjS1tEVrW3vku+VrG6K9o6PHmKoVAAAAAIDcEa5QNGqz9F0phOqVZdmWBNNvBQAAAAAgZ4QrFI2ayizhSgE0tX99dWYz+ynjVa4AAAAAAOSKcIWiUVM1KmOsvrEl8t3razIrVyarXAEAAAAAyBnhCkVjJC0LNnmccAUAAAAAIFeEKxSN6gIMVzo6OjIqV0aVl8b4MVU5mxMAAAAAQLETrlA0arMsC9aQ58uCra9vjsbmth5jk8ZWR2lpSc7mBAAAAABQ7IQrFI2aLJUr9XleuWJJMAAAAACA/CNcoWjUVGZZFqyptQCb2dfmZC4AAAAAAGwhXKFoFOKyYK9nqVyZonIFAAAAACCnhCsUjYJcFmxNfcbY5PHCFQAAAACAXBKuUNThSkOehyvZKlf0XAEAAAAAyC3hCkW+LFj+hivNLW2xen1jj7Fd6iqiOkvvGAAAAAAAdh7hCkWjurIsY6w+j3uurFi7OTp6jem3AgAAAACQe8IVikZZaWlUVfQMWDY35W/lyutrsiwJNr42J3MBAAAAAGAr4QpFpbZX35VkWbD2jt71Iflh2eoszexVrgAAAAAA5JxwhaJSXdmz70oSqzTmafVK1soV4QoAAAAAQM4JVyjqypV8bmqfLVyZMl64AgAAAACQa8IVikpNlnClPg/DlY6Ojli2ume4Ul5WGuPHVOVsTgAAAAAAbCFcIYo9XGlobIl8s76+ORqb23qMTRpXHaWlJTmbEwAAAAAAWwhXKCq1VT17riQa8rDnyuu9qlYSU/RbAQAAAADIC8IVikqhLAu2LFsze/1WAAAAAADygnCFolJTWRgN7bNVrkxWuQIAAAAAkBeEKxSV7MuC5V/PldezVK5MGV+bk7kAAAAAANCTcIWiUjDLgq2uzxhTuQIAAAAAkB+EK0Sxhyv5tixYS2tbrF7f2GNsl9qKqM6ypBkAAAAAADufcIWiUpNlWbD6xvxaFmz52s3R0Wtsimb2AAAAAAB5Q7hCUanLtizY5vyqXNHMHgAAAAAgvwlXKCq11VkqVzbnV+XKsizN7IUrAAAAAAD5Q7hCUSkvK42qirIeY5vyLFzJWrkyvjYncwEAAAAAIJNwhaJT16t6paGpNdra2yNfvL6mPmNssp4rAAAAAAB5Q7hC0cm6NFhjfvRd6ejoiNd7LQuWVNtMGFOVszkBAAAAANBTZnfvPLNmzZq4/vrr4/77748lS5ZEdXV17LXXXnHaaafFBz/4wSgr67nE0466+uqr47rrrotp06bF3Llzt7nvqlWr4sYbb4wHHnggnVt7e3vsscceccIJJ8Q555wTo0ePHtK5MTyVK519V8bUVESubahvjs1NbT3GJo2rjtLSkpzNCQAAAACAAgpXFi1aFGeeeWasXLmya6y5uTmeeOKJ9HHHHXfEnDlzoq6ubkiu99hjj6VBTn/84Q9/iM997nOxcePGHuMvvvhi+vjFL34RP/zhD2P33XcfkrkxvOFKvvRdWZat34pm9gAAAAAAeSVvlwVraGiIc889Nw1WJk6cGFdddVU8/PDDce+998b555+fVqwkAcsll1wyJNfbtGlTXHTRRdHW1rNqIJsXXnghPvWpT6XByqRJk+LKK6+M3/3ud3HXXXel4+Xl5Wkly2c/+9l+nY+dq64qf8OV3kuCJYQrAAAAAAD5JW/DlZtvvjkWLlyYBhU33HBDnHLKKTF+/PjYc88948ILL4xLL7003e+ee+6Jxx9/fIevd9lll8XixYv7te9Xv/rVaGpqSkOfm266Kd797nenIcs+++wTn//857sCn3nz5sVDDz20w3NjaNVWlxdUuDJFM3sAAAAAgLySl+FK0tQ76WWSSEKV2bNnZ+yTLBc2Y8aMdPuWW27Zoevdd999cdttt6XhzTHHHLPNfZ9++um0YibxpS99KeuyX+9///vTpcoqKirimWee2aG5sbN6rrTm8bJgtTmZCwAAAAAABRSuJBUfK1asSLePP/74rPuUlpbGcccdl24njeeTQGYwkmXHvvzlL6fbX/va12LcuHHb3P/uu+9On5OG9yeffHLWfZJQJenJkgQxF1xwwaDmRXH2XHl9TX3GmGXBAAAAAADyS96GK50OOOCAPvfbb7/90ud169b1e0mv3pLlxdauXRtnnHFGnHDCCdvdPwlMEkceeWTGe62tW6sfqqqqBjUfijdcaWlti1XrG3uM7VJbETVVmcuYAQAAAACQO3kZriTN4BNJv5XJkyf3ud/UqVO7tgcTrvz4xz+OBx98MK1C6ezhsj0vvfRS+pz0fkn8/Oc/jw996ENx8MEHx4EHHphW0/zzP/9zbNiwYcDzYeeozbosWO7DleVrN0fvAixVKwAAAAAA+Scv/yQ+qSRJJH1LysrK+txv9OjRXdvr168f0DXmz58fV155ZZSUlMTll1+eXmt7mpub0yqZRG1tbXziE5+IBx54ICMYuv7669Plw2644YaYOXNmDIexY2vSuZMsEVfS9TyuH/1JWiLz59bY2t6vY4fT80syf4f3nDom5/OCkWyg9w+AhHsHMFjuH8BguX8Ag+X+UYDhyrXXXhvXXHPNgI45/fTT44orroimpqb0dWVl5Tb37770Vucx/ZEs33XRRRfF5s2b46Mf/WjWJb6yqa/f2g/ju9/9btqvJekJk/RV2XvvvWPNmjVx2223xX/8x3+kIcsnP/nJuP3226O6ujqGWnl536FTsUrCprKy7QdOu47O/L3a1NAcZWW5LeRauiqz38ruk8bkfF5QDPp7/wDozr0DGCz3D2Cw3D+AwXL/KJLKlW1VqwxV8PPUU0/FrFmz4sILL+z3cY2NW/thJMHKu9/97rT6pVOyhNmnP/3pdJmxJLxZsGBB/PSnP42PfexjQ/4ZWlvbVK68IUldk59FR0dHtLf3Wlcri4ry0igrLYm2bvtuqG+Otrb2yKXFyzdljE0ZX5PzecFINtD7B0DCvQMYLPcPYLDcP4DBcv/Yaqj/iH3YwpUzzzwzTjzxxAEd07nMV2elx/aqUbqHHf1tIP/kk0/Gddddl/ZzSYKR7VXHdNf9GsnxF198cdb9ktAlWRLshRdeiHvuuWdYwpW1axuG/JyFKilnS1LX5OawZk1m9UdffVeSQKXTxobmWL16U04Dq4XLMvv01FWU9vszATvn/gHg3gEMlvsHMFjuH8BguX9sNXHi1jYjeR2ujB07Nn0MxpgxY7qW4UoStb6+8N64cWOP621PQ0NDWlHS1tYWn/3sZ9MG9AOR9FnplCwDNm7cuD73fctb3pKGK6+88sqArsHOMbpXuNLa1hFNLW1RVZGbYq7k9/z1Xje38rKSmLDL0C8pBwAAAADACFwWbMaMGelzS0tLrFixIiZNmpR1v6VLl3ZtT5kyZbvnffrpp2PhwoXp9re//e300ZekZ8rs2bPT7aSnShLGVFRUxG677ZbOaXsVL3V1dRnVNeSPpHKlt02bW3IWriRBz+amth5jk8bWdDWcAgAAAAAgf+Rlp+x99923a3vevHl97vfcc891VbpMnz59p8xtv/32S58XL16cVhv0ZdWqVelzX8EQuVWXJVyp39waufL6msxl3iaPq8nJXAAAAAAAKMDKlX322SdtCp9Uj8ydOzeOPfbYjH3a29vj/vvvT7ePPvrofvXKOOKII+Lxxx/f5j5f/epX484774ypU6fGXXfdlY6NGrX1i/hjjjkmHnzwwVi9enX86U9/Spf/yja3P/7xj+n2m9/85n58Yna2uuryrJUrubJsdZZwZbxwBQAAAAAgH+Vl5UoSlJx22mnp9m233dZVodLdzTffHAsWLEi3zz777H6dt6ysLO2bsq1H0qi+cw6dY8lyYJ1OPvnkriW/vvGNb6R9YXr7wQ9+kAZDiTPOOGNQPwNysyxYrqhcAQAAAAAoHHkZriTOO++8dEmtpO9KEp7ceuutsXLlyli0aFFcffXVcdlll6X7nXjiiXHwwQdnHJ80rj/ppJPSx1Dadddd4+KLL063k9DnQx/6UPzmN79JlwGbP39+fPOb34xvfetb6fvJtd/2trcN6fUZvmXB8i5cUbkCAAAAAJCX8nJZsERSHXLdddfFOeecE2vXro1LL700Y5/DDz88rrzyyqzHL1u2LA07hsP73//+2LhxY1x11VXx4osvxmc+85mMfZKlyv7pn/5pWK7PjqurytZzJZfLgmVWQE1RuQIAAAAAkJfyNlxJ7L///nH33XfHnDlz0t4rS5cujdLS0pg1a1aceuqpcdZZZ/Xoh7IzJaFPEqD86Ec/SvurrFixIg2E9t5773jve9+bzi9ZhozCqVzZmKNwpaW1PVatb+wxNqa2ImqyBEAAAAAAAOReSUdHR0euJ8HArVy5MddTyBvjxtVGWVlptLW1x5o1mRUg2by4aF1ccdPjPcb+Yv9Jcf5pB8TOtmTlpvjyDY/2GNt3913j4rMO2+lzgWIzmPsHgHsHMFjuH8BguX8Ag+X+sdXEiaOjKHquQLH0XFm2OrPfyhT9VgAAAAAA8pZwhaKUT+FK1mb2+q0AAAAAAOQt4QpFqbY6s92QcAUAAAAAgP4QrlCUykpLo7qyZ8BS32hZMAAAAAAAtk+4QtGq61W9srmpLVrb2nfqHDo6OjIqV8rLSmLCLtU7dR4AAAAAAPSfcIWila3vSn1j606dw4aGltjc1POau42tidLSkp06DwAAAAAA+k+4QtGqzYOm9q+vrs8Ym6LfCgAAAABAXhOuULSyVq7s5HBlWbZm9vqtAAAAAADkNeEKRauuKh8qV7KEKypXAAAAAADymnCFopWtcmWnhysqVwAAAAAACo5whaJVV5OflSt6rgAAAAAA5DfhCkVrdE1FxtjGhuaddv2W1rZYuX5zj7ExtRVRk2W5MgAAAAAA8odwhaI1Jkvlyob6nVe5snzt5ujo6DmmagUAAAAAIP8JVyhaddkqVzY353ZJMP1WAAAAAADynnCFopWtcmXjTqxcWba6PmNs8vjanXZ9AAAAAAAGR7hC0aqtHhUlJbmrXFm2RuUKAAAAAEAhEq5QtEpLSmJ09aiMnisdvRuhDJNl2ZYF03MFAAAAACDvCVcoaqNre/ZdaW1rj8bmtmG/bhLg9O65Mqq8NMbtUjXs1wYAAAAAYMcIVyhqvStXEhsbhn9psLUbm6KppWeIM3lcTVpNAwAAAABAfhOuUNTG9KpcSWxoGP6m9vqtAAAAAAAULuEKRW10dWa4srF++CtXei8J1lm5AgAAAABA/hOuUNRG12ZZFmzzTqhcWV2fMTZlfO2wXxcAAAAAgB0nXKGojanJsizYTqhcWZalcsWyYAAAAAAAhUG4QlEbXZNZubJhJzS0fz1Lz5VJlgUDAAAAACgIwhWK2ugslSubhrmh/eam1li7sanH2PgxVVE5qmxYrwsAAAAAwNAQrlDUclG5snytJcEAAAAAAAqZcIWiNqZ25/dcydZvZbIlwQAAAAAACoZwhaJWU1ke5WUlOQ9XVK4AAAAAABQO4QpFraSkJKN6ZWNDS7S1tw/bNV9fXZ8xNnl87bBdDwAAAACAoSVcoejt0itc6XgjYBkuy9aoXAEAAAAAKGTCFYreLrWVGWPrNw3P0mDt7R2xvFe4Ul1ZlhHwAAAAAACQv4QrFL2sTe0bhidcWbV+c7S2JbUxW00eV5suTwYAAAAAQGEQrlD0slWNDFflimb2AAAAAACFT7hC0dulLku4Ut80LNcSrgAAAAAAFD7hCkUva+VK/fBUrry+pj5jLFkWDAAAAACAwiFcoehla2i/YZjCFZUrAAAAAACFT7hC0RtTt3N6rnR0dGSEK6UlJbHb2OohvxYAAAAAAMNHuELR26Vm5ywLtqGhJTZtbukxNmlcdZSX+c8QAAAAAKCQ+FaXoldZURZVFWXDHq4sXbkpY2zqeP1WAAAAAAAKjXAFsjS139zUGs0tbUN6jaVZ+q1MnSBcAQAAAAAoNMIVyBKuDEf1ypJV9Rlj0yYKVwAAAAAACo1wBdKm9pXD3tTesmAAAAAAACODcAUiYmyWcGXtpqYhO39HR0dG5UppSUlMGlczZNcAAAAAAGDnEK5AEq6MzhKubBy6cGVDQ0vUN7b2GJs0rjpGlftPEAAAAACg0PhmFyJi19GZPVfWDWG4knVJMM3sAQAAAAAKknAFdsKyYEtXN2SM6bcCAAAAAFCYyiPPrVmzJq6//vq4//77Y8mSJVFdXR177bVXnHbaafHBD34wysrKhvR6V199dVx33XUxbdq0mDt37jb3/fWvfx233HJLPPvss7Fp06YYM2ZMHHTQQfGBD3wgjj/++CGdF4W9LFjvfiuJaROFKwAAAAAAhSivw5VFixbFmWeeGStXruwaa25ujieeeCJ93HHHHTFnzpyoq6sbkus99thjaZCzPW1tbfHFL34xfvnLX/YYX716dTzwwAPp4/TTT49vfOMbUVqqOKgQ7JqlcsWyYAAAAAAAZJO33/w3NDTEueeemwYrEydOjKuuuioefvjhuPfee+P8889PK1aSgOWSSy4ZkusllScXXXRRGpxsz7e//e2uYOWYY46Jm2++Of7whz/Ej3/84zj66KPT8Z///Ofxne98Z0jmxvCrGFUWtVXlGcuCdXR07PC5k3P0rlwpLSmJyeNqdvjcAAAAAADsfHkbriSBxcKFC6O8vDxuuOGGOOWUU2L8+PGx5557xoUXXhiXXnpput8999wTjz/++A5f77LLLovFixdvd7+mpqb44Q9/mG6//e1vj+9+97tx2GGHxYQJE+Lwww+P733ve3HEEUek7yfzTiptKMylwVpa26O+sXWHz7uhoSXjPJPGVUd5Wd7+5wcAAAAAwDbk5be7yV/633jjjel2EqrMnj07Y59kubAZM2ak20nfkx1x3333xW233ZaGN0klyra8/PLLaVVN4n3ve1+UlJT0eD+pqEl6riTq6+vT/SkMu44enqXBLAkGAAAAADCy5GW4Mm/evFixYkW63Vdj+KSXyXHHHZduJ43nB7t8U7Ls2Je//OV0+2tf+1qMGzdum/t376HS2pq9qmHUqFFZ9ye/jc3SdyVZGmxHLV29JYzrbppwBQAAAACgYOVtuNLpgAMO6HO//fbbL31et25dv5b0yiZZXmzt2rVxxhlnxAknnLDd/ZNqmdGjR6fbt99+e0aok7xOqmASY8eOjZkzZw5qXuR+WbDE2iGoXFmicgUAAAAAYETJy3BlyZIl6XPSb2Xy5Ml97jd16tSu7cGEK0kD+gcffDCmTZvW1cNle6qrq+OCCy5It5Mm9p/5zGfiySefjNWrV8dTTz2VvvfQQw+ly4VdfPHFUVmZ+YU9xRWuLFqRGa5Mm1i3w+cFAAAAACA3yiMPJZUkibq6urSHSV86K0gS69evH9A15s+fH1deeWUaglx++eXptfrrYx/7WNTW1sa//du/xW9/+9v00d3ee+8dF1100Xb7t+yIsWNrMvq9FKvS0pKu53HjBl8RssfUXTLGNjW17tA529o7YvHK+h5jo8pLY/9ZE6JMQ3sYMfcPoLi4dwCD5f4BDJb7BzBY7h8FGK5ce+21cc011wzomNNPPz2uuOKKaGraUi2wvaqPqqqqru3OY/oj6ZWShB+bN2+Oj370o3HkkUcOaJ5tbW3R2NgYNTU1Wd9ftmxZPProo/HWt741rXQZDuXlfYdOxSoJm8rKBh84TR6feXNZtW7zDoUgr6/ZFE0tbT3G9pw8Oioq8jLXhKK1o/cPoDi5dwCD5f4BDJb7BzBY7h9DLy+/4d1WtcpQBT/JEl6zZs2KCy+8cEDHJsHM5z//+bjvvvvSZcs+/elPp/1akuXLli9fHr/4xS/iO9/5TsyZMyddLuz666/vM4TZEa2tbSpX3pCkrsnPIul3097eswfOQIzfZWtY12nFms3R1tY+6HO+snhdxtiMKbvs0DmB/Lt/AMXFvQMYLPcPYLDcP4DBcv/YaqhXEhq2cOXMM8+ME088cUDHdC7z1Vntsb1qlKR6JFsVy7Ykgcd1112XBiPJsmAD7Yny85//PA1WEt/61rfiXe96V9d706dPT3uwHHLIIfHxj388/vSnP8UPfvCDdGyorV3bMOTnLFRJOVuSuiY3hzVrei7BNVB11aNi0+aWrtcr1zXEqtWbonSQQda8V1dljO22S+UOzxPIv/sHUDzcO4DBcv8ABsv9Axgs94+tJk7c2mYkr8OVsWPHpo/BGDNmTPpcX1+fJmp9VWhs3Lixx/W2p6GhIV0OLFnW67Of/WwceOCBA57bz372s/T50EMP7RGsdHf00UfHO9/5zrjnnnviJz/5ybCEKwyPpHqle7jS2tYRG+qbY9e6gYVwnV5bntnMfvfdNLMHAAAAAChkedlRe8aMGelzS0tLrFixos/9li5d2rU9ZcqU7Z736aefjoULF6bb3/72t2P27NkZj6QyJbFkyZKusWTfTgsWLEifDzvssG1eK+m3kkjmv2lT5hfs5KcJYzIroFat31ohNVCLVghXAAAAAABGmrwMV/bdd9+u7Xnz5vW533PPPddV6ZIsybUzJIFPorm5ud/HDGRfcitb35XVgwxXkgqYtRt7Lm03fkxV1FSNGvT8AAAAAADIvbxsaL/PPvvEtGnT0uqRuXPnxrHHHpuxT3t7e9x///1dy3D1p7n7EUccEY8//vg29/nqV78ad955Z0ydOjXuuuuudGzUqK1fhs+cOTMNdR555JFtnifpt5IYN27coJdHY+dLwo/eVm9oHLKqlT0mqVoBAAAAACh0eVm5kgQlp512Wrp92223dVWodHfzzTd3LdF19tln9+u8ZWVlUVtbu81H0ui+cw6dYxUVFV3n6Oyz8tJLL8V//dd/Zb1OErwk/VYSJ598cr+CH0Ze5cqi5Vt7AnWyJBgAAAAAQOHLy3Alcd5558WkSZPSZbiS8OTWW2+NlStXxqJFi+Lqq6+Oyy67LN3vxBNPjIMPPjjj+KRx/UknnZQ+htJHPvKR2HvvvdPtr3/96/HlL385nnrqqVi3bl3Mnz8/rr322jj//PPTypqkD8ynP/3pIb0+hV25IlwBAAAAACh8ebksWKKuri6uu+66OOecc2Lt2rVx6aWXZuxz+OGHx5VXXpn1+GXLlqVhx1CrqqqKOXPmxGc+85l49tln42c/+1n66G3GjBlp0JIsC0ZhV64MtqG9cAUAAAAAYGTK23Alsf/++8fdd9+dhhlJ75WlS5dGaWlpzJo1K0499dQ466yzevRD2VmSipSf/vSncfvtt8evfvWrdNmyjRs3pkuIJf1ikmqa97///VFdXb3T58aOqa0qj+rKstjc1NY1tnLd5mjv6IjSASzv1trWHktX1/cYq6ooiwm7+p0AAAAAACh0JR3/P3v3AR/JWef5/9s5qJWlUZic89jjccTZxtiAA4YFk8wC5oDdI3MLLAv334Vlj+Nu95ZwS2YJCxyLMcHgjG1wHNvjODnPSBqNclbn7v+rSrFVrdBSSy21Pu+ltqqfeqr6kWZUnunvPM8vmUzmehDIXEuLtZ7HYlVWViCHw654PKH29tRAYzr+4d+f1akx9VL+91+/SmVplgybaNbK//eDZ1La1i0r1mffuWvG4wMwf58fABYHnh0ApovnB4Dp4vkBYLp4foyorCzUoqi5AuRKVZl1dklTe39G9zh1lmL2AAAAAAAAAJCvCFeAMZaU+i1tTR3BjO5x4my3pW1lVXaTUQAAAAAAAABAbhCuAGNUlVpnrpzNcObKyUZruLK6pmhG4wIAAAAAAAAAzA+EK8AY1WXWmSvNGcxcMYrZGzVXRnM77aqtsN4XAAAAAAAAALDwEK4AY1SlCVeaOqY+c8UIVmLxZErbiupCOez8uAEAAAAAAABAPuDTXmCMgM+lAq8zpa2lM6hEIjUwyWhJsGqWBAMAAAAAAACAfEG4AkyhqL0xE6WtOzSla4+nrbdCMXsAAAAAAAAAyBeEK0AaVWXWovZnWvumdO3RBorZAwAAAAAAAEA+I1wB0lhaUWBpq29JLVKfTnd/RE3tqfVZCv0uLSm1hjUAAAAAAAAAgIWJcAVIY1llwNJW3zL5zJVj9V2WtnVLi2Wz2bI2NgAAAAAAAABAbhGuAGksX5ImXGmefObKkTThyvplJVkbFwAAAAAAAAAg9whXgDRKCz3ye5wpbY1t/YrGEhNed6Sh09K2bllx1scHAAAAAAAAAMgdwhUgDWMZr2VjZq8kkkk1to2/NFg4Gtepsz0pbS6nXSurCmdtnAAAAAAAAACAuUe4AoxjeZq6K3UTLA12pK5TsXgypW11TZEZsAAAAAAAAAAA8gef+gLjWLakIKNwZf/JDkvblpWlWR8XAAAAAAAAACC3CFeAcSxfYl3O61iDtWD9kP0n2y1tW1aXZX1cAAAAAAAAAIDcIlwBxrGiKiD3mHulRfMAALXUSURBVCW9Tp7tMWurjNXdH9HpMbNavG6HVtdQbwUAAAAAAAAA8g3hCjAOp8OuNbVFKW3xRFInznRb+u47YZ21smlFqRx2fsQAAAAAAAAAIN/wyS8wgXXLSixtR+o7LW17DrVY2rayJBgAAAAAAAAA5CXCFWACG5YXW9qO1KfWXQlH4tp7vM3S79x1FbM6NgAAAAAAAABAbhCuABNYW1ssmy217XB9Z0rdlVeOtykSS6T0WV1TpPJi71wNEwAAAAAAAAAwhwhXgAn4PE6tqk4tSh+JJvTKsZGZKk/vb7Jcd/7GyjkZHwAAAAAAAABg7hGuAJPYtXGJpe2ZAwOBSmtXUC8csdZb2UW4AgAAAAAAAAB5i3AFmMQFm6zhysvH2hQMx/TI8w1KJlPPrV9WrCWl/rkbIAAAAAAAAABgThGuAJOoLPFpdc2YpcFiCf3swcN65IUGS//rzl8+h6MDAAAAAAAAAMw1whVgCi7aXGVpe2LvWYUiI4XtDWVFHu3cUDGHIwMAAAAAAAAAzDXCFWAKLj+nVsUF7kn7XX/BCjns/FgBAAAAAAAAQD7jU2BgCnwep9545ZoJ+6xbWqxrdy2bszEBAAAAAAAAAHKDcAWYoku312jbmrK05/wep+64cbPsdtucjwsAAAAAAAAAMLcIV4Apstts+tCt2/WaC5bLMSpE2bSiRH/3rl2qKvXndHwAAAAAAAAAgLnhnKP3AfKC2+XQW69drxsuWqGj9V2qLvdrWWUg18MCAAAAAAAAAMwhwhVgGkoCHp2/aUmuhwEAAAAAAAAAyAGWBQMAAAAAAAAAAMgA4QoAAAAAAAAAAEAGCFcAAAAAAAAAAAAyQLgCAAAAAAAAAACQAcIVAAAAAAAAAACADBCuAAAAAAAAAAAAZIBwBQAAAAAAAAAAIAOEKwAAAAAAAAAAABkgXAEAAAAAAAAAAMgA4QoAAAAAAAAAAEAGCFcAAAAAAAAAAAAyQLgCAAAAAAAAAACQAcIVAAAAAAAAAACADBCuAAAAAAAAAAAAZIBwBQAAAAAAAAAAIAOEKwAAAAAAAAAAABkgXAEAAAAAAAAAAMgA4QoAAAAAAAAAAEAGCFcAAAAAAAAAAAAyQLgCAAAAAAAAAACQAcIVAAAAAAAAAACADNiSyWQykwsAAAAAAAAAAAAWM2auAAAAAAAAAAAAZIBwBQAAAAAAAAAAIAOEKwAAAAAAAAAAABkgXAEAAAAAAAAAAMgA4QoAAAAAAAAAAEAGCFcAAAAAAAAAAAAyQLgCAAAAAAAAAACQAcIVAAAAAAAAAACADBCuAAAAAAAAAAAAZIBwBQAAAAAAAAAAIAOEKwAAAAAAAAAAABkgXAEAAAAAAAAAAMgA4QoAAAAAAAAAAEAGCFcAAAAAAAAAAAAyQLgCAAAAAAAAAACQAcIVAAAAAJhD0Wg010MAAAAAMEOEKwAAAADyzjXXXKONGzea23xy11136ZOf/GSuhwEAAABghpwzvQEAAAAAYGJ9fX364Ac/qGeeeUYXXnhhrocDAAAAYIaYuQIAAAAAs6yjo8MMVgAAAADkB8IVAAAAAAAAAACADBCuAAAAAAAAAAAAZIBwBQAAAAAAAAAAIAMUtAcAAACQ99rb2/WDH/xADz30kBobG+X1erV69Wq95jWv0W233aaCgoIJr08mk7r//vt177336uWXX1ZbW5vcbrdqamp08cUX661vfavWrl1ruW737t1617veldJm1F7ZuHGjeWwUt//JT35iue748eP63e9+p2effVanT59WV1eXbDabioqKtH79el1++eV685vfrEAgMOPvDQAAAIDM2ZLG3xIAAAAAII9cc801amhoMI9/+ctf6gMf+IAZsKRTVVWlf/mXf9H555+f9rxxn49+9KN65ZVXxn0/h8Oh97znPfrkJz8pu90+Ybgy2thwJRqN6otf/KI55kQiMeHXWFZWpn/7t3/Tzp07J+wHAAAAIPsIVwAAAADkdbhSXFxszvww9sZMlaVLl5qzV4yZKJ2dnWYfv9+vn/70p9qyZUvKferq6vS2t71NLS0t5uuSkhJdffXVWrlypUKhkDmL5amnnjJnthhuueUWfeUrXxm+3nife+65R93d3frWt75lti1fvty8p8GY+fK6171uuP8nPvEJ/eEPfzCPnU6nLrvsMm3atMmcWWPc46WXXjJnswy9X2Vlpe677z5msAAAAABzjHAFAAAAQF6HK0MzRL761a+asz2GdHR06CMf+Yi5TJfBWKrrN7/5zfDMk3g8bi4ZNjRj5aabbtLf//3fW4IMI2D50Ic+pKamJvP1P/3TP+lNb3pTSp/6+npde+21Ey4F9vTTT+sv//IvzWNj+a8f//jH2rx5s6WfMRvGmIkTDAbN1//zf/5PveENb5j29woAAABA5ihoDwAAACCvGTNFjFkjo4MVQ2lpqb75zW+as0cMhw4d0qOPPjp83pjZMhSsGHVVjBkp6WaI7NixQ9/4xjfMmiiG//t//68ZzGTq17/+9fDxhz/84bTBiuGiiy7SrbfeOvx67969Gb8XAAAAgJkhXAEAAACQ14xZJeMVrDfCEqNWyhCjiPyQO++8c/j4/e9/f0otlXQBy6WXXmoeGzNm9uzZk/E4b7jhBn384x83C9XffPPNE/Y1ZtkM6evry/i9AAAAAMwM4QoAAACAvGUEItddd92EfYwaKkOee+45cx+LxfTCCy8Mt4+txZLO6MLy0wlXjHF88IMf1D/+4z+atV3G09/fby4zNsQYKwAAAIC55Zzj9wMAAACAOV0SbLxZK6P7eDwehcNhs3C9MROkra3NDDGGGMuCZcIoZD9TxjhOnDih06dPq66uzjw+ePCgjhw5khKoUEYTAAAAmHuEKwAAAADyVnFx8aR9jFopRgF5I1gxdHd3q7Ozc0bvO93rE4mEfvvb3+pnP/uZWUvFeJ2Ow+GYVl0XAAAAANlBuAIAAABg0Rs9+8PtdqcEF4WFhfqrv/qrjO63cuXKac1UMerDPPnkk5bwp7q6WuvWrdO2bdt04YUXmsuCff7zn8/4PQAAAABkB+EKAAAAgLzV09MzaR9jdogxW2WIMYvF2EYHL3fccYdm25e+9KXhYMVYyuxd73qXLr/8cm3atMmytNlPf/rTWR8PAAAAgPERrgAAAADIW2fOnDHrkzid4//Vx6hlEolEzONVq1bJ5XKptrbWvMa4tre3V01NTaqqqprwvYx+xqwXY8uUcf/f/OY3wzNV/v3f/13nnHPOuP07OjqGj6m5AgAAAMw9ew7eEwAAAADmhFGkfs+ePRP2efDBB4ePzz//fHPv8/m0devW4fYHHnhg0vf65Cc/aQYiV155pe68886Uc0ZgMpFXXnlleCmyzZs3TxisGHbv3j18TLgCAAAAzD3CFQAAAAB57etf//q4xd9bW1vNWSJD3vzmNw8fv+ENbxg+/s53vqP29vZx3+PZZ5/Vo48+ai4xZsxCGRuOGAXoh6Qby9DMGUNnZ+eEX89DDz2kZ555Zvi1MbsGAAAAwNwiXAEAAACQ14zg43Of+1xKgDG0ZNj73ve+4TDjqquu0rnnnjt8/o1vfKNWrFhhHjc3N+u9732vTp8+bbn/Cy+8oI997GPDr6+//nqtX78+pU8gEBg+Pnv2rCVgMeqqjB7Xj370I8v7GMHNL3/5S3OGzGjBYHAK3wUAAAAA2WRLMoccAAAAQJ655ppr1NDQoMrKSvX396uvr0/V1dW67rrrVF5ebtZZMZYDM84Zli5dai7lVVZWlnKf/fv3653vfKd5vcGox2KEMEYYYiw5tm/fPj3xxBPD/ce7j+Giiy5KCXJ27dplLj92++23m2133HGHHn/88eH+O3fuNDcjmDFmw/z5z39WY2Pj8Dii0ah5vGPHDjN0AQAAADB3CFcAAAAA5G24YtRN+fjHP66PfvSjwwHJWEY48Y1vfGPcgvWHDx82Z6YcO3Zswvc0gpB//dd/NUOcdP7lX/5F3/72t1PaCgsL9dxzz5nHbW1tes973qNDhw5N+D4bNmzQl7/8Zd12221mwGIENMYyYW63e8LrAAAAAGSPM4v3AgAAAIB55/LLL9dvf/tbff/73zdnfxhLfBmhxpYtW3TTTTfp5ptvlt1unzDMuPvuu3Xvvfeahe337t1rBiHGMl0VFRXavn27brzxRr361a+e8D5GQFNSUqK77rpL9fX15tJgxcXFZi0XY6aLMaPGmIHyi1/8Qvfdd5+OHj2q3t5eeb1ecwaOMVvGeI/Xvva1cjqduvjii/XYY4+Zy4Ldf//95tcCAAAAYG4wcwUAAAAAAAAAACADFLQHAAAAAAAAAADIAOEKAAAAAAAAAABABghXAAAAAAAAAAAAMkC4AgAAAAAAAAAAkAHCFQAAAAAAAAAAgAwQrgAAAAAAAAAAAGSAcAUAAAAAAAAAACADhCsAAAAAAAAAAAAZIFwBAAAAAAAAAADIAOEKAAAAAAAAAABABghXAAAAAAAAAAAAMkC4AgAAAAAAAAAAkAHCFQAAAAAAAAAAgAwQrgAAAAAAAAAAAGSAcAUAAAAAAAAAACADhCsAAAAAAAAAAAAZcGbSGfNHS0tProcwb5SW+uV0OhSLxdXR0Z/r4QBYQHh+AJgOnh0ApovnB4Dp4vkBYLp4foyorCxUNjFzBQuezWZL2QPAVPH8ADAdPDsATBfPDwDTxfMDwHTx/Jg9hCsAAAAAAAAAAAAZIFwBAAAAAAAAAADIAOEKAAAAAAAAAABABghXAAAAAAAAAAAAMkC4AgAAAAAAAAAAkAHCFQAAAAAAAAAAgAwQrgAAAAAAAAAAAGSAcAUAAAAAAAAAACADhCsAAAAAAAAAAAAZIFwBAAAAAAAAAADIAOEKAAAAAAAAAABABghXAAAAAAAAAAAAMkC4AgAAAAAAAAAAkAHCFQAAAAAAAAAAgAwQrgAAAAAAAAAAAGSAcAUAAAAAAAAAACADhCsAAAAAAAAAAAAZIFwBAAAAAAAAAADIAOEKAAAAAAAAAABABghXAAAAAAAAAAAAMuDMpDMAAMB8kUwmZf5fMjnw2vy/gXalOTb2I9cOH6WcGeo5shu5Zuxr6z3G9B3pkHI+tdkyspQ+I/cc02/UTSzXTvL+6cZnvcfE34fpmMk9xnwpGb9ztq9sTXrlsNsVTyTU3R3K7nvO4GvNxq/TtN53Rr9A07s2N18pMHNFMa/sDrsS8YS6e9I9PyZny/qogLnE7+DpKop7ZbfblRj3zx+YTTYbv3exMLkdLhWXrJPDwRyL2UC4AgBYlIwPAxPJhBLxuCKxmIKxoOLG6zHbxG3xwWPjXvEp9E8MhwGpx8ZRYuB4sM1sSQ61JUa1GecTo45H9R1z75T7jgoi0p43zxn/f+DT3cGj1ODC7D/8auT1qHbjnkM9hq4f+r+B/41tH+w9+vXg/QauGXU86joAAAAAADC5kleK9d+v+qhqAlW5HkreIVwBAGSV8cF9LBFTNBEbtY+a+7HHcfO1EVAMbEPHw22JuGLJmPmvs2Lm65gZVBj3tfZLPU4MtRnvMU7wAQAAAAAAkM86Q1362Su/1ScveX+uh5J3CFcAIM8Z/9LfCCMiiagi8Yi5hRPGfvD1qPah1+F4RFHjvNlvJBBJDU2iw69HHxsBBwAAAAAAAOaHzmBXroeQlwhXAGAehiFGSBGOhxWMhcx9KBZSKB5WOBZW0NiPagvFwoP7ob7GeSMkGQpMoiyjBAAAAAAAsEhdvfpVuR5CXiJcAYBZCkiMoKM/FlR/NDiwHz7uVzAaVJ/5un/4nNE2dMySVViIbIMFSo1ijwP/Z74Yah1sH+o35rX5P9uYY+PygaJ7Q3exm4UkR+5tH9Xf+h4jhSfNfoPXjIw39WjompGdLX2/lFqWE/cZvueY71G6cVj6jimaOd74Jh5j6tc20jx23Gm+ljF9xo5vIRUCndnYrdd6PA7zazGf9eH0s/Vm8qVm43s95++bg6+XsrKYK9n8Jyoej3PU8yOWxTtjvuAfNSFjU/wtw/MDBp4xyJTb4daFK3foouXnKh7ns6ZsI1wBgCkwwg4j9OiN9Kk32qfeSK96or3m657h1wN783y0j4BkHjA+sHPYHXLaHLLb7HIM7oc2l9Mph33gWHHjg3vjvG34/Oj+jlHXWdsc5rHxl53JrjHGZLzHUAAx1Ga8Hvd4ODQYbJ/g2pF7G+831G8wtjDHMPF9BgKNlHjCEmgMvRr6oHz0MbAYlJUVyOGwm385aW/vy/VwACwgPD8ATBfPDwAzeX5gdhCuAFjUjH/10xfrV1e429w6B/ddkaHXXebeCFIIS9IzQwq7Uy67S06709wGXhvHrnGPnUboYRwbwYTdaQYRxmsjnDACD6fNCD6M0MLoN7AfOJf6evjYDFEGwhKHzXiPgZBjIvwFBQAAAAAAANNBuAIgr8UTcTMwaQ+1qy3UobbgwL7d3DrNEMUoxJ6PjBDDmP7ptrsH9g7X4LFLHodbLrtbHqPNPOeWx+6Wa/Cc2z7SboQmA4HIQIDicowcDwQjjlx/qQAAAAAAAMCcIlwBkBcBSkuwTU39LWrubzH3QyFKR7hzQc04MQILv9Mnr9Mrr9Mjr8MzcOzwyGMep7YZr412n9Obct4IRSabtQEAAAAAAABgeghXACwYkXhUjX1n1dB7Vk39zYNbi1qD7fMqQDGWqAq4ClTg8svn9Mnv8pmByfDe6be0+QbbjBkiAAAAAAAAAOY3PsUDMC8ZdU7qehrU0NtobvW9jeaslKSScz4WYwZIoSugQnfADE3MvbtAAaPNVaCA2zhnvB5oM2aRUNwbAAAAAAAAyF+EKwByLhqPqq73jE50ndKJ7tM62XXaXM5rLhiBSLGnSMXuIpUYe3MrHjh2DxwbwQlLbAEAAAAAAAAYQrgCYM4FYyEd7Tyuwx3HdKzrpOp7ziiejM/KexmzTMq9ZSr3lqrMW6py38CxsZV6S83i7gAAAAAAAACQCcIVALMulojpeNdJHWo/qkMdR3Wqpz6rNVKM2iZV/kpV+ZeY+yXmVmEGKEZhdwAAAAAAAADIJsIVALOiP9qvfW2H9HLrPu1vO6RQPDzjexY4/VoaqNGywlrVFFQPBiqVZv0TAAAAAAAAAJgrhCsAsqY70qPnm17WS637zGW/ZjI7xVjCa2XRci0L1GpZoMYMVUo8xRSKBwAAAAAAAJBzhCsAZiQUC+mlln16tukFc8mv6QQqLrtLK4uWaXXRSq0qXqHVRSvMwvIAAAAAAAAAMB8RrgCYltPd9Xqs4Sk91/SiIoloxmHK2uJV2li2ThtK12p5YKkcdsesjRUAZlsymRzcm/9/1PHAy+TA/xs4M/j/hs+Pc93QPVPvZd5p1L2sfazXjXqjsfcb9+uxtKTpNEmPtJdMdlHmY5nsa0l/z8kvmqhLsDciu92uRDyhru7gBDfR4sZk07zDDOKZC/ZG5XDYFI8n1T3R82MO8cuKbOI5MXvC/THZ7TYlEvPn+QHMFI+M2ed0OVRa6s/1MPIW4QqAKYvEo3qu6QU91vC0TvfUZ3StsazX9vLN2li2XquLV8pl5/EDzJTxAbHxl6tE3NgnzA9qjA97zbZEUnHjOG58iD/wOjnYbnxoPLAfaU/pY3xwP7Zt9Ouh682+g9ePOh77HmYQYJwbs09pHwob0vQbr33oe5D2fqOv0+T3G7rXyDd3JLwYnU+kDTwAAAAAAJinSsv9esf7L1ZxqS/XQ8k7fLoJYFL90aD+3PCUHq17XD3R3ildY7fZtb5kjXZUbNX2is0q95XN+jiB2WR8qB6LGgFGQrFYQnFjiw/uY4NtQ68H95Z+Q9fGk8PXDQQgA4GIGY4kBgIRY4sPHZsBSkLxwf1IoMKn+wAAAAAAYHwdbf166Pf79abbd+V6KHmHcAXAuLrCPfpj3Z/0eMPTCscjk/a3yWYu83VB9Xk6p2KL/C6mHWLuGWFFNBJXJBwb3kcicfM4Fo0rGjX2CXPvdNjNgCMcjqmvN5JyfuyxEYoAAAAAAAAsNN2dLCc4GwhXAFgEYyE9dPpPevj0n6dUT6W6oEqX1Jyv86vOVYmneE7GiPxkzMQwwpBQMKpwKKZwKKpQMKaIcTwUlkRiioZHQpOxIYoRlgAAAAAAAGDA9vOW5XoIeYlwBcCwaCJmFqm//+TD6o32TdjXaXNo55IdumzpxWZxegoXYiwj5Aj2RxTsjw5uEQX7ogqFogoPhyepQUokHM/1sJFnjEeT+Xwa3A+9HnhkDb0eOB4qvj3ycvC6UY2jH3UDTQMNQ+3Dz8KUe5l3Gmkbuial36j3H/teY/qkjCd16OOOZ9JHdJoOtkkaJr1isv5pxjT4FU3YJ+X0JDedyn+aJrtHupdut9P83hrLBUaisTHn+e/hYjNYmSn/LZIvc7a/VM+o50c4kvr8yIlF8+u6aL7QnKIe3exK+fPHfHh+5Dl+P88Fvslzwel0aPP2Gu04fxlLi88CwhUApoPtR/SLQ79Wc7B1wn4FLr+uWnapLl96iQrdgTkbH+bPklv9vRH19YaH90ZgMhScjIQpEYKSLHM4bLI77LLbjb1NjuHjgb153j5y3mh3DB3bbbIZm23weOzeruHXRj/70H64beR8Sj/zeMy50deNOpcu3JiwfTAYMA/TnE8NR8a/HzAbysoKzJ9B45nY3j7xP0YAgNF4fgCYLp4fAGby/Bj4+zHhSrYRrgCLXHekR3cd+b2ebXphwn5l3lJdu+IKvarmArkd7jkbH+ZONBJTT1dYPd0h9fWEB7ahIKVnMEjpn3yZuHzjcjvkdNrldDnkdNnlcjnM4MJoM/5y4zDOOe1miGG2DW5GPRf74H64zeyXeu1QaDIcjgyGIWPDEwAAAAAAAMwfhCvAImVMJX6y8Rn9+ug9CsbGL2pV7C7U61Zfp0tqLpDD7pjTMSJ7zKnjYSM8CQ1uAyHK0Ove7pBZ22QhMwILl8dhTpd3exxyDe5HXhvhiMMMR4yQxDguLfXL43WZIUcwGBlodw71HQhAmP0AAAAAAACAsQhXgEU6W+WnB+7U3rYD4/bxOb26bsVVunr5ZcxUWUCMuiWd7UF1dQTV1d4/sO8Imm1GuDKfGQGIEXR4fU5z7/Eae6c8vsFjjxGSOM3gw9i7h/aDwYkx6yNTTK0HAAAAAADAdBCuAIvM3tYD+smB/5ywYP2ltRfq5rWvVcBVMKdjw9RnoRizTdpb+9TR2m/uu8xApX/ezD4xAg+f3y2v3yWfubnlK3DJ5xtoGx2geH0uMyRh6SsAAAAAAAAsFIQrwCKRSCb0h+MP6L5TD4/bp7agWm/b9EatKV41p2PD+CGKUffECE/aWwZClA7juLVPsWhizsdjhB8FAbf8hR4VBIzNrYJCj3wFbvkLBgMUIzjxu8yltQAAAAAAAIB8RbgCLAK9kT79YN9PdajjaNrzTrtTN65+ja5Zfjl1VXIYpBjLd7Wc7VHL2V61Ng3s52opL6OIemGRV4EijwqLjb1XBYXuwRDFYx4bM0yoPwIAAAAAAAAQrgB572xfs7750g/UGmpPe35ZoFZ/ueWtqg1Uz/nYFnOQ0t0ZVFNDtxmgGIFKa3OvopH4rIYnRSU+Mzgxt8EQZeDYK3/ATXACAAAAAAAATBHhCpDHDrUf1Xf3/kTBWDDt+WuXX6Gb1t4gl51HwWyKRuNqaexR05luna3v0tkz3Qr1R2dl2a7CEq9KSn0qLvWruMzYD2zGTBRqmgAAAAAAAADZwSeqQJ7a0/SSfrj/52atlbG8Dq9u3/IWnVu5LSdjy3ehYFRnTnea29mGbrU19yqRSGbt/g6nXaXlfpVVFKisskClFX6VlheosNgju92etfcBAAAAAAAAkB7hCpCHnjizWz8/eJeSsn6gX+1fog/s+Est8VfmZGz5KByK6kxdl86c6lTD6Q61Nfdl5b7GKl0l5X6VVwbMEKXMCFEqCszlvZiFAgAAAAAAAORO3ocrhw4d0ve+9z3t3r1b7e3tKikp0bZt2/T2t79dV1xxxbTu+cMf/lD/43/8j0n7vfe979WnP/3pab0HMF0P1z2mXx25O+25TaXrdce2d8rv8s35uPKJMQul+Uy3Th9vNzej+HxyhhNTjLDECFAqqwtVURUw98Zrl8uRrWEDAAAAAAAAyJK8Dlf++Mc/6qMf/aii0ZHaBi0tLXrkkUfM7fbbb9fnPve5jO+7d+/eLI8UyI5H654YN1h5Vc2FeuvGW+Ww82H9dPT3RVQ3GKbUnWhXOBSb0f1KynyqXlqsqqVFA0FKRYG53BcAAAAAAACA+S9vw5X9+/frE5/4hBmsbN++XZ/61Ke0fv161dfX61vf+pYeeugh/eQnP9Hq1av1jne8I+N7G97//vfrgx/84Lj9XC7XjL8OYKqePPOMfnnkt2nPvWbl1bp5zQ2yGetMYco62vp14nCLThxuVXNjz7Tv43TZtaSmSNXLilRdOxCoeH08HwAAAAAAAICFKm/Dla9+9asKhUJauXKlfvSjH6mgoMBsLy0t1Te+8Q197GMf03333aevfe1ruuWWWxQIBKZ03/7+fp04ccI83rlz5/B9gVx6rulF/ezgr9KeM0KV61ddM+djWoiSyaRam3rNMOX44RZ1tPZP6z5uj0M1y0q0dGWJaleUqHxJAYXmAQAAAAAAgDySl+HKsWPH9Oijj5rHH/jABywBiPGv9z/zmc/ogQceUGdnpx588EHdeuutU7r3gQMHlEgkzGNjRgyQa4c7junH+3+Rtnj9G9fdqGtXTK+20GIKVNqae3V4X5OOH2xRT3d4WjNTapYVa+nKUjNQMWqmEKYAAAAAAAAA+Ssvw5XHHntsOES5+uqr0/apqanR5s2btW/fPnOJsKmGK0NLghnXV1ZWZnHUQObO9jXpO6/8WPFk3HLupjXXE6xMoLc7ZAYqxjadGSql5X6tWFOmFWvLzFkq1EsBAAAAAAAAFo+8DFeM2SWG2tpalZWVjdtvy5YtZrhibFM11Hfbtm2655579Ktf/UqvvPKKuVxYdXW1rrjiCr3vfe8z3xuYTd2RHv3bSz9QMBZMW2PlhlXX5mRc85lRhP74oRYzUDlzujPj2SnLVpaaYcqKNeUqLPbO2jgBAAAAAAAAzG95Ga40NDSY+2XLlk3YbygAOXv2rGKxmJxO55TDFWPZMWM5sdHq6ur005/+VHfddZf++Z//Wddey4fbmB3xRFzfe+U/1BbqsJx7Vc0FZp0VjCz71XSmWwdebNTRg82KRQeW9ZsKt8epVevLtWZDpZavLpXT5ZjVsQIAAAAAAABYGPIyXOnoGPjAubi4eMJ+hYWFwx++dnd3TzjLxRAOh3X8+HHzOBqN6oYbbtC73vUurV692rzeqOHyzW9+05zF8tGPftQMWs4555ysfV3AkF8f/YOOdZ2wtG8qXa+3bnyjuSTeYhcORXVkX7P2v3hGbS19U77OV+DS6vUVWrOx0ixG73Cw3BcAAAAAAACARRCuGCGIwePxTNjP6x1Z1icSiUx63zNnzqiqqsqc6fLXf/3X+tCHPjR8zghm3v/+9+vCCy/UO9/5TjN8+cIXvmAuGzYbSkv9fIA+yG63De/LygqU7544/aweqX/c0r68uFZ/c8UH5Hf5tJi1NvXo2SdO6pU9DYpGrbVo0nG7Hdq0o0bbdi7VyrXlw7+nkP8W2/MDQHbw7AAwXTw/AEwXzw8A08XzY/bkZbjicMzO0j3GDJWHH37YDE5cLlfaPueee65uu+02/cd//If27t2rgwcPatOmTVkfi9PJ8kRjGWGTw5HfH4rXdZ3Rd/b81NIecBfo05f/tQq9i/MBacw+O3aoRbsfO65jB1umdI3xH5S1m5Zox3lLtWFrlVzuvHwcYooWw/MDQPbx7AAwXTw/AEwXzw8A08XzI/vy8tNEn883pdkooVBo+HiyWS6jjResDDFqrRjhiuHll1+elXAlFoszc2XUh+TG98L4gD2RSCpfReNRffWpHygSj6a022TThy98j8q9pYrHp15PJB/EYwm9vKdezzx2Qq3NvVO6prK6UDsvXK4t59aqIDDyc7/YvndYXM8PANnFswPAdPH8ADBdPD8ATBfPjxHZXv4/L8OVoVoqPT09E/Yz6qQMzXSZrD5LJmpqaoaP29vbNRs6Ovpn5b4LkTGdzUhdjYdDe/vUa2ssNL86crdOdzVY2m9cc72WuVfk9dc+lrHc14GXGvXi7jr19QwsAzgRp9OudZuXaPO5NaqqLTL/gxKOxBRuj83JeDF/LZbnB4Ds4tkBYLp4fgCYLp4fAKaL58eIysqB3CBb8jJcMZbveuaZZ8waKRNpbGw090YdFbt96qmVkfJNNGvEWDZs7CwaYCYOtB/Ww3WPWdq3lm/Sa1ZelZMx5UIkHNPe5xv00rP1CvWnzuBJp6Tcr+3nLdX6rUvk8U484wwAAAAAAAAAFnW4smHDBnNfV1en3t5eBQKBtP32799v7jdv3jyl+/6v//W/dNddd5nLiT399NPjLiV29OjR4eNVq1ZN4ysARvRH+/WT/b+wtBe6A7p981tkt2V3Ott8FI3E9cqeer3wdJ0ZsExm+epS7bhgmZavLmP5PAAAAAAAAABZl5efyl555ZXmPh6P69FHHx131sqBAwfM48svv3xK9y0tLTWX+erv7zfDlfHcfffd5t7v92vXrl3T+AqAEb8++gd1RaxL3N2++TYzYMlnRh0UY6bKz769W7v/dGLCYMXhtGvLuTW67X0X6MbbztGKNeUEKwAAAAAAAABmRV6GK8uXLx8ONb7+9a9baq8Yy3p9+ctfViKRMAOTW265ZUr3fe1rXztczP4rX/mKIpGIpc/vf/97Pfzww+bxW9/61nFnzQBTcaj9qJ5sfNbSftWyS7W1fKPylbEG5OG9Z/X/vvuMHnvgiPr7rD9rQ1xuh3ZevELv/KuLdeUNG1VWUTCnYwUAAAAAAACw+ORluGL427/9W7OOysmTJ/X2t79djz/+uDnrZN++ffrwhz+s++67z+xnHBszTEa74YYbzO1Tn/pUSvvSpUv13ve+d3jpr7e85S3605/+pNbWVh07dkz/+3//b3360582z69du9a8NzBdkXhEPzt4p6V9ia9Ct6x9nfLVmbpO/epHe/TH3x9Ud2do3H4er1MXXL5Kt//1xbr4qjXyF7jndJwAAAAAAAAAFq+8rLli2L59u770pS/p85//vA4fPqw77rjD0uc973mP3vGOd1jaT5w4Ye4rKyst5z72sY+ps7NTv/jFL8xlxd7//vdb+hg1XL797W9bQhsgE3848aBaQ+2W9rdvepPcjvwrzt7TFdLTjx7T0QMtE/bz+pw69+IV2razVi533j7CAAAAAAAAAMxjef3J5Bvf+EZt3bpV3//+97V79261tbWZgce2bdvM2SyvfvWrM76nMRvmC1/4grlE2M9//nO98MIL6ujoUEFBgdavX6/Xv/71evOb3yynM6+/tZhlZ/ua9HDdY5b2y2ov0vrStcon0WhcL+6u04tPn1Yslphw+S+jSP25Fy6X28PPFwAAAAAAAIDcyftPKDdu3GjWR8nEoUOHJu1zySWXmBuQbUZNoDuP3K1EMjVoKHYX6Q3r8ms5sFNH2/TYA4fV0x0et4/dYdO2nUt13qtWyOdn6S8AAAAAAAAAuZf34Qqw0Lzcul8H2g9b2v9iw83yOX3KB0aB+iceOjLpEmDrtyzRRVeuUWGxd87GBgAAAAAAAACTIVwB5pFoPKpfHbnb0r6hdJ12Vm5XPszKOfjyWT31yDGFQ7Fx+1VUBXTZdetVs6x4TscHAAAAAAAAAFNBuALMI4/UPa62MUXs7Ta73rz+ZtlsNi1kXR1BPXrvIZ053TluH5/fZc5U2bSjesF/vQAAAAAAAADyF+EKME/0Rfv1wOlHLO2XL71EtYFqLeTZKgdeatQTfzyqWDR9wXojR9m2a6kuuGy1PF4eSwAAAAAAAADmNz7FBOaJB089qmAslNJW4PLrxtXXaSHXVvnTvYd08mjbuH3KKgt01Ws3qqq2aE7HBgAAAAAAAADTRbgCzAOd4S49Wv+4pf2GldfI7/JrITp1tE2P3HNQwf5o2vMOh03nX7ZK51y4XA6Hfc7HBwAAAAAAAADTRbgCzAP3nHhI0URqgfdST4m5JNhCE4vG9cTDx7T/hTPj9qldXqwrX7tRJWULMzgCAAAAAAAAsLgRrgA51tzfqqcan7W0v37Na+RyuLSQdLb364Hf7FNbc1/a83aHTRdfuUY7LlhGwXoAAAAAAAAACxbhCpBjD5x6RIlkaqH36oIqXVR9nhaSYweb9cg9hxSNxMetrfLqmzarfElgzscGAAAAAAAAANlEuALkUFuwQ7vP7rG037TmetltC6MOSTye0FMPH9MrexrG7XPOhct04RWr5XQ65nRsAAAAAAAAADAbCFeAHHro9J8ss1aWBmp0TsVWLQTB/oju//U+NdZ1pT3vD7h17Y2btWxV6ZyPDQAAAAAAAABmC+EKkCNd4W492fiMpf36ldcsiHokrU29uu9Xr6inO5z2/NKVJXr1zVvkL3DP+dgAAAAAAAAAYDYRrgCSItG4Tjf1qq6lVz19EcUSSfncDlWW+LSiulBLSnxZf88/1v1ZsUQspa3KX6mdS7Zrvjt2sEUP/+GAYtHUWTdDzr90pXZdukp2+/wPiQAAAAAAAAAgU4QrWLSSyaQO13XqkRca9OLRVkXGCQoMlSVeXbCpSlecU6Mlpf4Zv3d/tF+PNTxtaX/Nyqvnda0V43v2/FOn9cyfT6Q97/E6dd0tW7R8ddmcjw0AAAAAAAAA5grhChal+uZe/fTBwzpU1zml/i2dId3z9Cndu/uUXrWtWrdctloVxdOfzfLEmWcUiUdS2sq9pbqgaqfmq0QiocceOKL9LzamPV9WWaDXvmmbimZhlg8AAAAAAAAAzCeEK1hUEsmk7n36lH7z2AnFE8mMr08mpSdeOavd+5v06l3L9YbLV8vtcmR0j3girj/VP2lpv3bFlXLYM7vXXIlGYnrgt/t1+lh72vOr11fomhs3ye3hkQIAAAAAAAAg//FJKBaNcDSub/92n7kE2EzF4knd98xpvXSsVe+7cYtW1xRN+doXW/aqI5w6Y8bn9Omi6l2aj/p7w/rDL18xC9ins+tVK3XB5atks1FfBQAAAAAAAMDiQLiCRaE/FNNX73xJR+q7xu2zsqpQW1aVqqrML5fTbha2P9XUo30n2tXdH017TWNbv7704z3mDJbXXbJS9ikEDI/UPW5pu7T2QnmdHs03PV0h3f3/XlJXR9ByzihWf9XrNmrjtuqcjA0AAAAAAAAAcoVwBXkvGovr6796edxgZduaMr3pirVaWV2Y9nw8kdCLR9r028dPqL6lN+1SY3f9+bgZxNzx+s3yusf/sTrRdVonuk+ltBkF7K9c9irNNx1t/Waw0tcTtpxzexy6/tZtWraqNCdjAwAAAAAAAIBcIlxBXksmk/ru3fvTFq53u+z6y+s36eKtVRMuaeWw27VrY6V2bqjQM/ub9J+PHFVnb2oxesOeQy1qau/Xh9+0Q5XjFHV/tN46a+Xcym0q886vkKK1qUd3/+JlhdLM2CkodOv1b96h8iWBnIwNAAAAAAAAAHLNnusBALPp3t2n9dyhFkt7kd+lz75zly7ZVj3lWiHGkl8Xb63WF+64SBdtqUrbp76lT//0kz063dRjOdcT6dULza9Y2q9efrnmk7MNXfrtz15MG6yUVvj1xtvPI1gBAAAAAAAAsKgRriBvHa7r1K/+dMzSHvC59Ol3nKcVVemXAZuMcf0Hbt6q/3LTFrmd1h+hrr6I/ufPnteh0x0p7bvP7lE8GU9pW1G4TKuLVmg+BSu//8XLioRTx2morA7olrefq0CRNydjAwAAAAAAAID5gnAFeSkYjul7v9+vZDK13QhDPv6Wc1RTXjDj97hka7X+9p27VF5kLUQfDMf1z794Sc8fbhlenuyJht2WfpcvvXjKM2dmW9OZbv3hP19WNGINVmqWF+vmt50rn9+dk7EBAAAAAAAAwHxCuIK8dOefjqm1K2Rp/8sbNml1TVHW3mdldaE+/5cXaG2t9Z6xeEL/99ev6LGXzuhI53E1B1tTznsdHp235BzNBy1ne/T7X7yUdsbKijVlev1bdsjtoUQTAAAAAAAAABgIV5B3TjR269HnGyztl++oMWusZFtRgVv/7a07tX1NueWcMXPm3+89qLv2PmI5d0H1efI6rbNechGs3P3/0gcrq9aV64Y3bZPL5cjJ2AAAAAAAAABgPiJcQV5JJJP6jwcOa8xqYCov8uqt166ftff1uB368Ju2m0uFWTgjOh0+Ymm+tPYi5VpHW79ZYyUcilnOrVxbrtfculUOB48JAAAAAAAAABiNT02RV5490GzOXBnr9us3yjfLy1o5HXbdceNmveaC5SntjvIzstlT456Vhcu1vLBWudTbHTKXAgsFo2mXArueYAUAAAAAAAAA0uKTU+SNaCyhX//5uKX9vA2V2rHWumTXbLDbbLrtmnV6w2Wrh9ucFdYlyi5deqFyyQhUjBkrvd1hy7nlq0t1/Ru3yuHk8QAAAAAAAAAA6fDpKfLGH589rebOYEqbwz4Qdswlm82mmy9brTdduUY2X4/sBT0p55Nxh1pPlilXopGY/vCfL5tLgo1Vu7xYN7xxm5xOaqwAAAAAAAAAwHgIV5AXYvGEfvXoUUv71TuXqrLEl5Mxvf6SVdp6XmrYY4h3LNFv/1yn3z1+Ys7HFI8ndP+v96m5MTXwMVRUBXTDm7bLSfF6AAAAAAAAAJgQ4Qrywp+er1dLR2qQ4XE5dOOrVuVsTIlkQm32Y5b2eNtArZXfPH7CXMYsmUytxzJbjPd5/MEjqjvRYTlXXOrT69+yQx7v7NalAQAAAAAAAIB8QLiCBc8IDX71yBFL+1U7a1VU4FauHOk4rs5wV0pbMuJRomuk/svdT57Ur/40NwHLS8/Uaf+LjZb2goBbN962Q/4cfq8AAAAAAAAAYCEhXMGC9/LRVtU19aa0OR12XX/hCuXSM03PW9pibTWWH7t7nj6lnz90ZFYDluOHWvTUI8ct7W6PQ6+/bYeKcrR0GgAAAAAAAAAsRIQrWPDufeqkpe3S7dUqCXiUK5F4RC82v2Jpf/2mV8mWpv9De+r1o/sOKpHIfsDS3NitP959wNJut9t0/a3bVF4ZyPp7AgAAAAAAAEA+I1zBgtbeHdIz+85a2q89b5lyaW/bQYXi4ZS2moIq3XzeOXrv6zenDVj+/FKjvvf7/YonElkbR19PWPfeuVexmPWeV96wQctWlWbtvQAAAAAAAABgsSBcwYL26IsNGjvZY8PyEi1bktvZGOlmrVxYdZ5sNpsu3V6j/3LzFtlt1ojl6f1N+tZv9ikWn3nAEo8ldP+v96m/L2I5d94lK7Rph7FEGQAAAAAAAAAgU4QrWLCisYT+/OIZS/s15y1VLkXiUb3SZl2G67yqHcPHF2+p1l+9YZscdmvAsudwi77+q1cUjsanPQajfstjDx5R05luy7l1myt14RWrp31vAAAAAAAAAFjsCFewYO051Kzu/mhKW3HArfM2VCqX9rcfMmuujLa8cKkqfOUpbbs2Vuojf7FDLqf1x/CV42365//3onqD0emN4cVGHXip0dK+pKZQV79ukzmDBgAAAAAAAAAwPYQrWLD2n+qwtF15Tq2cjtz+tn6h+WVL287K7Wn7bl9Tro+/+Rx5XA7LuaMNXfof/7FHbV2hjN6/sb5Ljz94xNLu87t0/a1b5UzzXgAAAAAAAACAqSNcwYI1NpBwOmy68tzcLgkWjUe1t9W6JNi5S9KHK4ZNK0v13956rnwep+VcY1u//uk/9qi+pXdK79/fG9YDv96nxJhCNHa7Ta95w1YFirxTug8AAAAAAAAAYHyEK1iwXnPBci0p8Q2HB3fcvE2lhZ6cjulgxxGF4uGUtqWBGlX5J16qbO3SYn3qbTtVVOC2nOvoCevL//G8DqSZqTOaEag8dPeBtAXsX3XtWtWuKJny1wEAAAAAAAAAGJ/1n8oDC0RliU//8N4L1RWOqaqswAxW2tv7cjqm5zNYEmysldWF+uztu/Qvv3hRzR3BlHP94ZjZ/o7rNuiqneln57zw1Ck1nOq0tG/cVqVt5+V2Rg8AAAAAAAAA5BNmrmBB87gd2rSyTBWDM1hyKZ6I65XW/Zb2nRMsCTaWMRPns+/cpVXVhWnun9SP7z+knz10WPFEIuXcmdOdevbxk5ZrKpYEdMX1GyhgDwAAAAAAAABZRLgCZMmxrhMKxlKLz1f7l6i6oCqj+xhLg33q7Tu1bXVZ2vMPPVevr/7yZfWHoubrYH9ED/1uv5KpZVbkcjt03Ru2UMAeAAAAAAAAALKMcAXIklfSFLLfUbl1Wvfyup36yF/s0JXn1qY9v/dEu/7hh8/qZGO3/vj7g+rrtdZZufKGDSop80/r/QEAAAAAAAAA4yNcAbJkb5pwZXvFlmnfz+mw613Xb9TbXr1e6Vb1aukM6bs/fl51x9st57acW6P1WzKbMQMAAAAAAAAAmBrCFSALmvpb1BxsTWkLuAq0qmj5jO5r1Eq57vzl+tibz5HPk7q8l1dS7di1wCSVVRbo0mvXzeh9AQAAAAAAAADjI1zBgpYIhdTx3B71nTo972atbC3fJLstOz9i29eU67O3n6+qUp/52pjIskY22c2jEXaHXa+hzgoAAAAAAAAAzCrn7N4emD3Rlhad/tIXFO/tMV+vuP2d8l756nkTrmyr2JzV91haUaD//u4L9O/3HlTjwRYVjAlWDMfjMT2yr0k3X7rKXFYMAAAAAAAAAJB9fPqKBav9gXuHgxVD/X/+UolQcM7H0R8N6mjXiZQ2Y8bK5rL1WX8vn8epN+xapto0wUqnkmqR9PsnT+pLP9mj+uberL8/AAAAAAAAAIBwBQtYvKsr5XUiHFaksXHOx3Gg/ZASyURK2/qSNfI5B5bwyqZIOKaHf3/Q0h5VUic0Un/l1Nke/cMPn9UvHz2qcDSe9XEAAAAAAAAAwGJGuIIFy1laZmmLtqUWlZ8Lr7QenPUlwYY8/afj6ukKWdpPKqnYmLZ4Iql7nz6tz39vt/Yeb5uV8QAAAAAAAADAYkS4ggXLVV5haYu2zm24kkwmdbDjsKV9W/mmrL/XmdOd2vf8GUv7pu3VevsbtqnAm76EUmtXSP/yny/p6796WU3t/VkfFwAAAAAAAAAsNhS0x4LlrKjI+cyVM31n1RNJrW1S4S3TEn9lVt8nFo3r0XsPWdoLizy69NXr5PY4tW5ZsX5070G9dCz9LJUXjrTq5WNtuua8Zbrp0lUK+FxZHSMAAAAAAAAALBbMXMGC5UoTrsTmeObKwfYjlrZNs1DI/tnHT6qrI2hpv/K1G81gxVAS8Ogjf7FDf/WGbSoucKe9j7FU2IPP1elvv/2U7nn6lEKRsYuJAQAAAAAAAAAmQ7iC/FoWrG0+hCsbsvoezY3deumZOuv7bK/W8tWpdWdsNpsu2LREX/ovF+vq85bKNs49+0Ix3fnoMX3qm0/p3t2nFI5Q9B4AAAAAAAAApopwBQuW3e+X3eez1Fwx6qDMhWgipiOdx1PabLJpY+narL1HPJ7QI/cc0tgvyV/g1quuHf99/F6nbn/NRv3du87XuqXF4/brDUb1y0eO6VPfelJ3P3nSfA0AAAAAAAAAmBjhChYsY5aGc8zslWQkonhvz5y8/4muk4omUsOIFUXL5Hf5s/YexoyV9pY+S/vlr1kvj3fymilraov0t+88z1wqrKLYO26/nv6ofv3n4/pv//aE/uOBQ2rqoPA9AAAAAAAAAIyHgvZY8HVXIvV1lrorzsKiWX/vA2mWBNtcmr16K92dQe154pSlfe2mSq3ZWDnl+wwtFXbuunI9tKde9zx1ylwWLJ1INKGHn2/QI883aPvacl15bq12rC2Xw04OCwAAAAAAAABDCFeQl3VXvKvXzPp7H2o/OqvF7B9/6KhisURKm8fr1GXXTe89XE6HXnvRSl117lL9cU+97n/m9Lghi7EK2cvH2syttNCjy3fU6NLtNaosSV2GDQAAAAAAAAAWI8IV5F+40jr7Re37ov063VOf0ua2u7SqeGVW7n/iSKtOHW2ztF989Rqz3spM+DxO3fiqVbp21zI99FydHnyufsJaKx09Yf3uiZPmZtRvuWhLlTkTpmiG4wAAAAAAAACAhYpwBQuasyL9zJXZdqjjqJLm/I4R60rXyGWf+Y9UNBLXEw9alxyrqi3S5h01yhYjZLnp0tV6zYUr9OTes3rgmdNq6ghOeM3Rhi5z+/lDR7Rldaku3FSlc9aVq9BP0AIAAAAAAABg8SBcwYKvuTKWUXNlth3tPD5r9Vb2PHlKPd3hlDabTbri+vVm/ZRs87gcunrnUrO+yktHWs26LAdOdUx4TSKZ1N7j7eZmDMmY0XLu+gqdu65CNeUFWR8jAAAAAAAAAMwnhCvIy5ors+1o5wlL24bSdTO+b0drn156ps7Svn3XMlVUFWo22W027dxQaW5N7f3680tn9PgrjerpH3/JMEMyKR2p7zK3Xz5yTFWlPm1ZXaYtK0u1aWWpCryuWR03AAAAAAAAAMw1whUsaHa/Xw6/T/H+YErNlWQyOSuzPIbqrZzpPZvS5nP6VBuontF9jTEbRewTidTlxvwBty64fJXmUlWZX2++ep3ecPkavXS0VU/vb9LLx1oVi6eOLR1jabGmjgY98nyDOatlZVWhNq8q1cblJVpTW6yAj7AFAAAAAAAAwMJGuIIFzQhQPJVL1H/q1HBbMhJRvLdHzsKiWXnP410nLfVW1havkt1mn9F9jQL29Sety3Fdeu06uT25+VF1Oe06f9MSc+sPRfXcoRbt3t+kg6c6xnwHxp/VcvJsj7nd+/Rps626zK+1S4u0dmmx1tUWq7aiQHb77ARhAAAAAAAAADAbCFew4HkqK1LClaG6K7MVrhxJU29lXcnqGd0zHk/oyYePWdqXrizR2k2Vmg/8XpeuOKfW3Dp6wnrxaKtePNKqA6fapzSjZcjZ9n5ze+KVgdk/XrdDK5YEtLyq0NyvqCpUbYVfLqdjFr8aAAAAAAAAAJg+whUseJ4lS9LWXfGuXjNn9VbWlczsvV55rkFdHSNLmxmMJbUuffW6WVvebCZKCz26eudScwtFYtp3ot0MWl4+3jZpjZaxQpG4Dtd3mdsQh92m6nK/llcGzH1NeYE548Wo5+J2EboAAAAAAAAAyC3CFSx4niXWmR1G3ZXZEIqFVdfTkNLmtru0onDptO/Z3xfRnidPWtq37KxVeWVA853X7dSujUvMLZFMqr65VwdOdZjbodOdCkfjGd8znkiqoaXP3EYzYqbyYq8ZuBhhS02ZXxUlPlUUe1Ve5CV4AQAAAAAAADAnCFeQtzNXZsOJ7lNKJBMpbWuKV8lhn/6H+s/8+YQi4dQAwqixcsFlc1vEPhvsNpu5rJexXX/hCsXiCR0/060j9Z061tCtow1d6g1mNrNlNGPxsdaukLntPd5uOV9U4DaDFjNsMfZFXpUEPCop9Jj7ogKXHPaZ1cYBAAAAAAAAAMIVLHieSuvMFaPmytwtCTb9eiutTT068FKjpd0IVnx+txY6p8OuDctLzM2QTCbV3BnUsYau4bDlTGufOVMlG7r7IuZmBDrpGDNfCgvcKgkYm2d4b4QyAZ9LhT6XAv6BY2NzOQliAAAAAAAAAFgRrmDBm8tlwY50ZK+YvRE0pCtiX1Lu19bzapWPjPoxVaVG7RS/XrWtxmyLxhJmwFLX3KvTzT2qazL2vQqGY1l//+SoAOZ0U++k/b1ux3DQEvAPhC9+j0s+r0M+j9Pc/IP71NcOeVyOeVkvBwAAAAAAAMDMEa5gwXMEAnL4/Yr39w+3RVtblEwkZMviElDReFSnuk+ntDltDq0sWjGt+9WdaFfDqU5L+6uuWSuHY/HMmDBmh6ysLjQ3qWY4eGrrCqmxvV9n2/p1tr1fjW195r6zNzJnYwtF4uZmLEM2nSXSjJDFCGiMWjDG5hne7OZ+qM1tvHaPnDfaXQ67+b1xOmxyOR2De7vZ7nQOnRt4bbcT4gAAAAAAAABziXAFC54xO8BbU62+YyOzSpLRqGKdnXKVlWXtfU73NCiWTK2NsrJoudwOV8b3SiSSevoR6yyY5WvKtHJtuRY749fULFRf4tP2NanfD2NGixGyGFtLZ9AMPowgxjju6AlnbYmxmUokk+oLxcxttjnstoGgZTiMsZu1ZRwOm3luYBsIYcxjo91m7AfanIPt5nmHce3IdcPX2G3mr4vx2piQY4RHxuuhYyPfsRn9jTYjXBqnny2lb7rzA7/+5t6408D/Bgy2DU0IGu4zdHq4fbA15dqBtrF9QvGkHE67+TPZ1RUc6DN47cBu9PsNHAy/ntVf1cUlGz+1yfnxoz/MCInni2wNJZmNX6msjSW394gkZT4v4/GEOjtH/nFHrsaT3Ztk62dy/vwMGLIxnOQ8Gkz2xjKvbrModIfj5p+Thv7sgcVrvj0nMf91hWLDf/7g+QFgqox/wFta6s/1MPIW4Qrygrc6NVwxRJubshquGMXsxzKK2U/HkX1Namvps7RfctWaad1vMTGW3lpdU2RuY8UTCXX2RNTaNRC6tPeE1dkbVldvxNwPHc+XACZbjK8nnogrHE0N/wAAAAAAALC4VZX59YUPXGIu04/sIlxBXvDVVFvaoi3N0qbNWXuPk12pS4IZVhevzPg+sVhczzx2wtK+cVuVypcEpj0+GDM47Cov9prbxglmlPQGo+o0g5eIunrD5uueYFS9/dHB48jw8VzMPAEAAAAAAABmQ1N7v374+/369O3n53ooeYdwBXnBWBZsrEhzc1bf48SYeiuGVdOot7J3T4N6u8MpbcYyTRdcvnpG48PUGEtPFfnd5raiavL+xmwYI2AZClv6wzFzabKhbeB1fMzrkc2o2cKMfwAAAAAAAOSKsZw+so9wBXkbrhjLgmVLR6hTneGulLZyb6mKPUYR9qkLh6J6/ilrSLP9/GUqLPbOeJyYndkwQ2HMdNdSjsUTCkcTikQHlu4yt0hckVjC3BuvB86N9InGE4rFEuY+GksoFh+4TzSlbbw9aQ4AAAAAAAAGXH3eslwPIS/lfbhy6NAhfe9739Pu3bvV3t6ukpISbdu2TW9/+9t1xRVXTPu+9fX1+u53v6vHH39cTU1NCgQC2rhxo9785jfrxhtvzOrXgKnVXBkr2tKStfuf7K7LyqwVI1gJj1lmyuN16rxLMr8XFgajCLrL6TA3+Vxz8p5GoDNQhyWpeDxpLoVmFD0cbhs+lxg8N7o9YRZYHdtm7I0ZOMa9E0P7dG3pzss4HjlvtJn7hJQwziZSrx+4p/mVDBTIHcyKkqMKfw7cd6Qo8FC/sX1Gf0+GXg6NyWD+ugwuFxeNps4ySvdew/eYtV+9xcs2T+4xcCPb/PmasvZFZe+ZNl9kYyjTvYXT5TC/F2aAbtS7mke/Z7L1g2DLwo3m0W+XLP5Mzp8vah4NZd59b+Yzt3vk+RGJUC9vseOnBplwjXp+RBfz84MfHCAjbqdDF++o0dW7lpuf0yC78jpc+eMf/6iPfvSjikajw20tLS165JFHzO3222/X5z73uYzv+/LLL+vd7363+vpGCpJ3dHTo6aefNrf7779f/+f//B85nXn97Z1X3KWlsrvdSkQiKTNXjD90ZOMveumK2a8qziwQ6esNm0uCjWUEKx7v3HzojsXB+D3vdBib8SfwXI9mfisrK5DDYTeDpvb2kWc6AEyEZweA6eL5AWC6eH4AmMnzY+DzUcKVbLMrT+3fv1+f+MQnzGBl+/bt+slPfmIGH3feeade/epXm32Mtp/+9KcZ3ffs2bN6//vfbwYrq1at0re//W099dRT+v3vf6+3vOUtZp8HHnhA//zP/zwrXxfSs9nt8lSnFtBIhEKK9/TMXjH7DGeuvPDUaXOZp9ECRR5t27V0xuMDAAAAAAAAAMydvA1XvvrVryoUCmnlypX60Y9+pAsvvFClpaVm0PKNb3xDN9xwg9nva1/7mnp7e6d83+985zvmLJWioiIznLnqqqtUVlam9evX64tf/KLe+973mv2Mc8bSYcj10mAzL2ofT8R1uif119Jpc2hZ4dRDkd7ukPa9eMbSfv6lq+QcXJYIAAAAAAAAALAw5OW6VceOHdOjjz5qHn/gAx9QQUFBynljGtRnPvMZc4ZJZ2enHnzwQd16662T3re7u9uc+WIwlhRbsmSJpc+HPvQhs4/R9ze/+Y35GjkMV5qb5Fu7bkb3behtVDSRWifFCFZc9qn/+Ox58pQSY4qMF5V4tWFb6mwbAMD8MlR7Z2T69HBRoOHaPQOvR58fOjf6/NA9hmoJpbaNLjBk9hj7vmbNH2vbmNGmfT3cOmn/0fce5x7prpniOEZ2E7xvBmO13GfMmCe6duz9049pfLaIW3a7XYlEQn194Yk7T/nW2Z6in5zFn4es3nWe3y/d78cZ3zB3PTP6Ulg2YjbE+4znh81c87y/f2RJYxj4PYc5Niv/XZs98T6P7DabWS+yf7I/f8yyhfWdm2/47mFu2ewuFXi3yF9o/RwbM5eX4cpjjz02HKJcffXVafvU1NRo8+bN2rdvnx566KEphSu7d+9WODzwH7Brr702bR8jyLnkkkvMuivGfQlX5o63xhquRJpnPnPlRPfMlgTr7gzq4MtnLe0XXLbKXC8VAGYqmUwomYxLybiSifjgcUJJJQb2yUTa16ltxh/yR/U19mNfp2sb/doMBRIjQYB5fjBQGAoghvsNvTZeDVyT0m/cvkOvp3ifwTEM9DW/W1MPSYBxtOV6AAAWrI5cDwDAgsXzA8B0ddbfp7XnvluBsg25Hkreyctw5cCBA+a+trbWXLJrPFu2bDHDFWPL5L5GofpNmzaN288IbYxw5fDhw4pEInK73Rl/Dcicp8o6CySajXAlTb2VTIrZ73nilPkv00YrLfdr3RZmrQALlfHBfTIZUzIRVTIRS3M8uCUH20b3GTw/EE7EB88NBiOD2/CxGZQkxj03dEwQAAAAAAAA0jE+Nzh78lGtI1zJurwMVxoaGsz9smXLJuxnhC9DRepjsZgZmkzlvtXV1XI4HJPeNx6Pm/desSKzwufI3syVaEvTjO97agYzVzrb+3Vor3XWyvmXrTKXAwAwy7M54mElzNAjYm6J+OB+sC3eZzMDj3gsrP6+PiWMfnHjvNFvoM/I8UhIYoQaAAAAAAAAC4GxwhOyLy/DFaPgvKG4uHjCfoWFhcP/AtmokTLRLJfp3NfQ1dWl2VBa6ueHYtBQSOFbUimb06FkbORDz1hri8rKUmvuZKI/GlRzsDWlrchTqHW1y6b0/f/zfYcty7guqSnUBZesko1wBRiX8Vw2gpBYtE/xWFDxWEiJWMjcj97StsWH9qxjDgAAAAAAFjebzaHq1Vebn6HO5HNSLJJwZaguisfjmbCf1+sdPjaW75qN+w5dk21O5/gzZxYru9Mpz5IlCp1pHG6LdfcoGQzKGZjeg+NUa72lbW3Zyil9/5vP9mjfS2cs7VffsElOF79+WFxBiRGQRMM9ikf7zcAkZuwjxnG/4kOvzbaBY6PfwHJXQCZsxp8aZRva24y6VsbeCLMH2gZ6jRynnDdfmmen0H+wz/C/ADL6DLVN3sdyz8H3HuozNIqUr2m4z9hxjPkejOpns7SPeZ1y5WR9hr6WdOfTX5ud909tH/neaAbvb71/+q8rG6Zwvym+ZfqvfX6Mbaodp367qfbM5vdkil9Dlr8nWb1Xzn4vIQX/CG4G+N5hbvE8nAG+dTPANw9zx+5wq7BsrTy+gUkFDge//7IpL8OViZbsmo/3nY5YLM7MlUFG6mp8L4wPcL3V1SnhiqHvzBkF1q6d1r2PtZ2ytK0uWa543CiQPLFH7ztoKYNQs6xYazdVTul6YCEEJrFIj6KRXsUGNyNAMdrM48G9sRGUZItNNrvD/Fcnxt5udw4f22zOlHPm3mYfCBgG9+lfOwZe29Odd0x6vVL6DQQaA8HB4OvB46FwISXwGN02um+6cCTt9SN9xw8bgNn9s8fYumoAMBGeHwCmi+cHgJmu+sPzQ3I4jM8UsicvwxWfzzel2SihUGj4eLLZKKPvO9lslNH3HT2LJZs6Ovpn5b4LkTGdzUhdzYdDSbnlfNvR04qUWuuxTMXBpuOWtgpnpdrb+ya8rq25VwdfsdZa2XnJCn7tMO+Z/7GNGbNHuhWLdiseMWacdA+8jhj7gddGHZLFxGZ3DQYYztTj4Tbj2DXqeLy+g33MUGMoBHEY/5xk+Hi8c/MtQBj6I1ly2h2m844EdZhff/aY7M8EADAazw8A08XzA8B08fwYUVk5Us4jG/IyXBmqedLT0zNhP6POytCMlMnqqBiKiorMfW9v75TuaygtLZ3SmJEdriVLLG2RJmvIMVV1vQ2WthWFyya9bs+T1hkv1UuLtGLNxHV9gLkMT2KRDsUinYqFOwf3HYob+2j3wi7YbrPL7vDKbvfI5vCYU2Btdrfs9oG9EW4MtLlUEAjI6fKaoUhfMJGmz8B1A0HH/Ak1AAAAAAAAkFt5Ga6sXr1azzzzjM6csda7GK2xcWD5qKqqKtntk08JWrVq1fB1xoeT433QNnRfp9OpysrKaXwFyGa4Em1umta9grGQmvtTi9kHXAUq8UwcxHW09enYwRZL+wWXr+LDWczxsl29ioVaFQ23KRZqM8MTM0SJdMzvWSdmOOKXw+mT3dgcxuY1t4GwxDMmPDHODeyN1+bskCn+rA386w27uVRfcpH/6w0AAAAAAAAs8nBlw4YN5r6urs6cZRIIBNL2279/v7nfvHlzRvc1lhs7evSo1q9fP+F9161bJ7fbPa2vAdPjrqqxtEUGw65M1fekn7Uy2Ye2zz912tJWtbRIS1cyiwnZl0zEFB0OUEaCFGOfTEy8NOLcsMnuNIKSgByuAtmdxuaTwwhMnP6B4MR4bYYofvPYnDlCEAkAAAAAAIB5LC/DlSuvvFJf/OIXFY/H9eijj+rGG29MO7vkwIED5vHll18+pfteeOGFZt2VYDCohx9+OG240t/fr6effjqj+yJ7XJWVsjmdSsZiw22RsxPPNBrP6bThytIJr+nuDOrIPutMmV2vWsmHxZj5TJRIpyKhZkWDTYoGm81jI0jJYkGLKTNmiThcRXK4ArIPBicOZ8Hg64G9EaiYYYlZgBwAAAAAAADIH3kZrixfvly7du3Snj179PWvf90MW4bqsAx9SPnlL39ZiUTCrIlyyy23TOm+BQUFuu666/S73/1OP/jBD3TTTTeptrY2pY/xfkbNFZfLpXe+851Z/9owMZvdLldVtSIN9cNtiWBQ8a5OOUsymzlyumfkHkOWFy2bdNZKcszn3BVVAWqtICPJZELRUIsi/Y2K9J9RJHjWDFPmaiaKMZvE4S6Ww1Uop9sIUAa2keNCsx4JAAAAAAAAsFjlZbhi+Nu//Vu95S1v0cmTJ/X2t79dn/70p7VlyxZzxso3v/lNPfjgg2a/D3/4w/L7/SnX3nDDDeZ+x44d+spXvpJy7hOf+IQeeughdXZ26h3veIc+85nP6IILLlBHR4d+9KMf6Re/+IXZ7/bbb1d1dfWcfb0Y4a6pSQlXhpYGyzRcqctw5kpvd0iHXjlraWfWCiYLUmLhNjNICRtBSv8ZRfvPKpkcmX2VbcayW053iZye0oG9u0QOj7EfeE1wAgAAAAAAACzScGX79u360pe+pM9//vM6fPiw7rjjDkuf97znPWZAMtaJEyfMfbpi9DU1Nfra175mhjJnzpzRRz7yEUsfI5z5m7/5m6x9LciMuzpd3ZUz8m/eMuV7hNIUsy9w+VXqKRn3mhd31ymRSJ22Ulrh1+oNFVN+X+S/RCKqSF+Dwn11CveeVrivXslEOOvvYxR1d3rK5PSWy+Upl8tbMfDaU2bOTCHwAwAAAAAAAKYvb8MVwxvf+EZt3bpV3//+97V79261tbWZs1S2bdtmzmZ59atfPa37GrVU/vCHP+g73/mOHn/8cTU1NZmF6zdt2qQ3velN5vvywWXuuGtSl2obqruSifreRiXH1LGYqJh9f29Y+1+yvgezVhCP9g0EKX2nFe6tM2eoSIms3d8ISly+JXJ5K80QZSBMqTCX9eL3HgAAAAAAADA78jpcMWzcuNGytNdkDh06NGmfpUuX6h/+4R9mMDLM5rJgY0Uarct1ZVxvZYIlwV56tl7xWOoH5sWlPq3dtCSj98XCl4hHzCAl1HNcoZ4TZvH5rLA5zNknLm+V3EaYYm5VZtF4QhQAAAAAAABgbuV9uILFx11lrXUTOXsmC/VW0hezDwWj2vu8tf95l6yQ3c6H3vkumUyadVJCPcfMMMWYpaLkDGem2Bxy+6rk9tcObjVmsGKzObI1bAAAAAAAAAAzQLiCvGP3eOQsL1esrW24LdbRoUQoKLvXN6V7NPRal/haXmhdbszw8rP1ikVTP0wvLPJo/daqjMeOhTM7xZiZEuw6rGD3ESVifTO6nzEbxVOwdFSQskQ2O0EKAAAAAAAAMF8RriBv666MDlcMkcZGeVevmfTaWCKms33NKW1eh0dl3lJL32gklnbWys5LVsjhsE9r7JifYpFuBbsOmYFKqPeklIxPu9C8u2CpPAUr5Aksl6dgmewOb9bHCwAAAAAAAGD2EK4gL7mra9S/9xVLUfuphCtN/S2Kj/ngvDZQI7vNGpbsf7FR4VAspc0fcGvjduvSZFh4YtEeBTv2q69znyJ91jo8U2Gze+QtXClPYKUZqLj91SzvBQAAAAAAACxwhCvI25krYxkzV6a7JNjSQI2lLR5PmIXsx9pxwTI5nXx4vlDFo73q7zyg/o59ZmH6jNns8hQsl7dwtbyFa8ylvmxpgjkAAAAAAAAACxfhCvKSu6Zm2uFKfe+ZKYUrR/Y3q68nnPq+Hoe2npu+Ngvmr0QiqmDnIfW1v2jWUsmUw10iX/EG+QrXmjNU7A73rIwTAAAAAAAAwPxAuIK8XRZsrEijNTRJ50zv2UnDlWQyqRd3W2c1bN25VG4PP1YLgfFrGOmvV1/bS+rr2KdkIjUom5jNrJViBipFG+T0Vshms83iaAEAAAAAAADMJ3wKjLzkKCyUvaBAib6+4bZIS7OSsZhsTmfGM1dqC1JrqJw62qaO1v7U93TYtOP8pTMeO2ZXIhZSb/tL6m3do1i4deoX2hzyFa2Vr3izfMXr5XD6Z3OYAAAAAAAAAOYxwhXkJWMWgTF7JXTs6EhjPK5oS3PaeixDuiM96on0prRV+MrldXpS2l5IM2vFKGLvD6T2w/wR6W9UT+tz6u/Yq2QiOrWLbHZ5C9fKX7JF/pKNsju8sz1MAAAAAAAAAAsA4QrylhGipIQrksJnGiYMV9IVs182Zkmwxvouna3vtvQ758LlMxovsi+ZTJjF6Xuan1akv2HK1xmF6P2l2+Qv3ii70zerYwQAAAAAAACw8BCuIG95llqX6ArX16tw1wUZhStj66288LR11sqajZUqKWOZqPkiEY+or+0FdbfsVjzSOaVrnJ5yFZSdo4KyHXK6i2Z9jAAAAAAAAAAWLsIV5C3PMutMknB93YTXTBautLf0mfVWxtp5MbNW5oN4tFc9Lc+ot/U5JeKhSfvb7C75S7crUH6O3P5lFKUHAAAAAAAAMCWEK1hU4UqkbjrhysgyYi+mqbVSu6JES2qY6ZDrUKW76QmzSH0yGZu0v8tbqUDF+eYsFbuDOjkAAAAAAAAAMkO4grzlKCyUo6RE8c6RZaGirS2KB4Ny+Kx1NGKJmM72Nae0eR0elXlLzOPe7pCO7E89b9h58YpZGT8mF4/2qbv5SfW2PDuFUMUuf8kmM1TxBFYySwUAAAAAAADAtBGuIK95lq1Q/6hwxRCpr5dv/XpL36b+FsWT8ZS22kCN7Da7ebz3+QYlEsmU8xVLAlq+unRWxo7xxWP96m56Ur2tzyqZiE7Y12Z3K1B+ngqXXCSnu3jOxggAAAAAAAAgfxGuIK95li1T/96XLXVX0oUr6ZYEWzZYbyUaiWnfC9bz51y0nBkQcyiZiKmn9Vl1nX1MyUlqqjicATNQCZTvkt3pnbMxAgAAAAAAAMh/hCvIa57l1iW7wvXWuimGxr4mS1tNQbW5P/jKWUXCqctOFRR6tHZTZdbGivElk0kFOw+o88wfFYt0TNjX4S5RcfXlKijdLpudRxwAAAAAAACA7OOTRyy6ovbh+vq0fRv7zlraagPV5lJgLz9rvWb7+UvlcAwsGYbZE+6rV0fDA4r0pf91G+JwF6u46nIVlJ8jm80xZ+MDAAAAAAAAsPgQriCvuaurZXM6lYzFUpYFSyYSstlTg5HG3nQzV6p08kirujtTl6ByuR3acs7AkmGYHfFYUF1n/qjetucn7OdwFau4+jIVlJ0rm51QBQAAAAAAAMDsI1xBXrM5HHLXLlX49KnhtmQ4rGhrq9xLlgy3heMRtYbaU64tdheqwOXXS88estx3045qebyuWR794l0CrL/jFXO2SiLWP24/m8NrzlQprLyA5b8AAAAAAAAAzCk+kcSiWBpsdLgyNHtldLhydpx6K01nunW2viul3ahfv+P8ZbM44sUrGmpVe909CveenKCXXYHK81VcfYUcTv8cjg4AAAAAAAAABhCuYHHWXak7rcLzdk1SzL5KLz9bZ2lfvaFCRSW+WRjp4pVMxtXd9IS6zj4mJePj9vMVb1JJ7bVyecvndHwAAAAAAAAAMBrhCvKeZ7k1XImMKWp/Jk0x+3JV6tDBFkv7ORdY74fpiwZb1Hb6t4r0nxm3j9NTprJlr5O3aM2cjg0AAAAAAAAA0iFcweKcuVJ/OuV1upkroWMeJZPhlLaq2iJVLyuehVEuPslkQj3NT6uz8ZHxZ6vYHCqqulTFVZdRVwUAAAAAAADAvMGnlch7jsJCOUpKFO/sHG6LtrQo3t8nh7/AfN3Ymxqu2ONONRzos9zrnAuptZINsUiX2k79WuHe1JBrNE9gtcqWv44lwAAAAAAAAADMO4QrWBS8K1aqb1S4YgidPKmCLVsVjIXUEU49V9uxXtFI6myKwiKPWW8FM9PfeUjtp3+nRDyY9rzN4VXZshvkL90um8025+MDAAAAAAAAgMnYJ+0B5AHvamutjtCJ4+b+7NglwZJS8dmllv7bL1gmu50fmelKJmJqr7tXrSd+MW6w4i1ap5pNH1RB2Q6CFQAAAAAAAADzFjNXsCh4V6+2tIVOnkhbbyXQVSFbvzulzeV2aPOOmlkeZf6KhTvVcuI/FQ2eTXveZnerdNn1Kig7l1AFAAAAAAAAwLxHuIJFwbtq/JkrZ/pSP/Ava1pl6btxW7XcHn5cpiPYfUxtJ+8ad7aK279UFaveKKendM7HBgAAAAAAAADTwafFWBQcgYBclZVmIfshRoH7aEdHSjF7V8inwq5Ky/XbdtXO2VjzRTKZVHfTE+pqfGRgrbU0iqouVXHNVbLZHHM+PgAAAAAAAACYLsIVLKq6K6PDFUP45PGUZcHKmlfKptRlqZauLFFpecGcjTMfJBJRtZ36jYKdB9KetzsDqlj5BnmLrDOKAAAAAAAAAGC+ozo3Fg3vKmvdlZ6jh9UV6TaPbXG7SluWWfps32Utbo/xxaO9aj7yo3GDFU/BctVsej/BCgAAAAAAAIAFi5krWFQzV8bqPX5EKh84LmmvlTOeWsg+UOTRynWDHTCpSLBZLcd/rnikK+35QOWFKq29TjY7y4ABAAAAAAAAWLgIV7BoeFaslOx2Y82q4bZ4Xb10frExb0VlTSst12zdWSu7cQ2mVLi+9cSdSibClnM2m1NlK25UQdmOnIwNAAAAAAAAALKJcAWLht3jkbt2qSL1dSNtoYhKeuIK2yrk6y9O7e+wafM5NTkY6cLT177XrLEijQRXo+urVK59qzz+2pyMDQAAAAAAAACyjXAFi4p39eqUcMVQ3RZVb8I6a2Xd5iXy+VOXCYNVT8uz6qi/N+05l7fKDFac7tTgCgAAAAAAAAAWMtY7ghZ73ZXKVpuK2qst7RSyn1gymVTX2T+PG6x4i9apasO7CVYAAAAAAAAA5B1mrmBR8a5abW3rWSZ7ILXAekVVQEtqiuZwZAsvWOlseEA9LbvTng9U7FLpstfKZiO/BQAAAAAAAJB/CFewqHiWLpPN41UyHDJfJ41lrVzrLP2otTJxsNJRf596W59Ne76o+nIVV18lm80252MDAAAAAAAAgLnAPyvHomJzOORbNxKm9HjK1espS+njcNq1fsuSHIxugQQrDfePG6yULH2NSmquJlgBAAAAAAAAkNcIV7Do+DduGj4+U7Tecn7txkp5vK45HtUCClZanklz1qayFbeoaMnFORgZAAAAAAAAAMwtlgXDouNbv9Hcx20OnQ1YC9yzJNj4NVbSByt2Vax+k/wlm3MwMgAAAAAAAACYe4QrWHQ8q1bJ5nKp2bNccYc75VxhiUc1y4tzNrb5qqvx0XGK1xOsAAAAAAAAAFh8CFew6NhdLnnXrNXZ7uWWc1vOqaVeyBg9zbvV3fRYmjM2ghUAAAAAAAAAixI1V7AohVasUrt/7PJfSW3cVp2jEc1Pfe2vmHVWrGyqWEWwAgAAAAAAAGBxIlzBonTCUS7ZUn/7F8ZbVVDoydmY5ptg91G1nfpt2nPlK2+Vv3TLnI8JAAAAAAAAAOYDwhUsSvVt1hXxlnYcViIazcl45ptwX4NaT/xSUsJyrnTZDSoo25aTcQEAAAAAAADAfEC4gkWns71f4Y7Uuir2RExVXScVPnlCi10s0qWW4/9PyYQ1aCqqvkKFlRfmZFwAAAAAAAAAMF8QrmDRObKvydJW0VcnZzKq/gP7tZgl4hEzWEnE+iznAhXnq7j6ypyMCwAAAAAAAADmE8IVLCrJZFJH9jdb2qt7jpv7vr0va7FKJhNqO3WXokFr+OQr2WwuB2azpc74AQAAAAAAAIDFiHAFi0prU6+6OoIpbc54SOX9DeZx6MQJxXt7tRh1nvmjgl2HLe1uf63KV75BNhuPCwAAAAAAAAAw8GkpFpUTh1stbUt6T8k+VLg9mVTfvr1abHrbXlRP81OWdoerWJVr3iq73ZWTcQEAAAAAAADAfES4gkXl+OGWtOHKaP17X9FiEulvVEfdPZZ2m92tyrVvlcMVyMm4AAAAAAAAAGC+IlzBotHR1q+O1v6UtoQ9otLg2ZS2vr2vKJkYnMmS5xKxoFpO/FLJZGzMGZsqVr1Rbl9VjkYGAAAAAAAAAPMX4QoWjRNpZq10lTarO5BapD3e063w6dPKd8lkUq2nfqN4pNNyrqT2WvmKN+RkXAAAAAAAAAAw3xGuYFHXW+kua9LJWrelvW/vy8p33U2PK9R9xNLuK9mswiWX5GRMAAAAAAAAALAQEK5gUejpCqm5sSelLWGPq7eoRQ1L/Zb+xtJg+SzUc1xdjY9Y2p2ecpWvuFk2W+psHgAAAAAAAADACMIVLAonjlhnrfQUtyjpSCiyulY2pzPlXOjYUcV7e5WP4tE+tZ78jaXdZnepYvWbZXd4cjIuAAAAAAAAAFgoCFeweJcEKx0oZF9eVCXfxk2pJ5NJ9b74vPKxzkp73d1KxKzBUdnym+T2LcnJuAAAAAAAAABgISFcQd6LhGM6W9+V0pawJdRT0mweV/kqFDj3PMt1Pc8+o3zT2/a8gl2HLe2BigtUULYtJ2MCAAAAAAAAgIWGcAV5r+FUpxKJZEpbf2G7Es6YebzEX6nAebukMXVG+g/sz6ulwaKhVnXW329pd3mXqHTpdTkZEwAAAAAAAAAsRIQryHunT7Rb2nqLW4aPl/gr5Cwuti4Nlkio9/k9ygfJRFytJ+9SMjkQKA2zOVS+6lbZ7Kk1ZwAAAAAAAAAA4yNcQV4zaozUHbeGKz3FIzVYjJkrhsILLrT2ey4/lgbranxE0eBAjZnRSmtfLbevKidjAgAAAAAAAICFinAFea2zPaierlBKW9QVUtjXYx4HXAUqcPkHjtMtDXbwgGI93VrIwn0N6m5+ytLuLVyrQKU1UAIAAAAAAAAATIxwBXkt3awVc0kw28iSYEOchUXyb9qSZmmw57WQlwNrP323cZTSbnf6Vb7yFtnGhEkAAAAAAAAAgMkRriCv1aWpt9Izut6Kb2BJsCGBCy6w9n/maS1UXU2PKRpqtrSXLb9RDlcgJ2MCAAAAAAAAgIWOcAV5KxaN68zpzpS2pJLqK24bfj165oqhcOcuyZ76YxE8dFCRFmtAMd9Fgk3qPvu4pd1fslX+kk05GRMAAAAAAAAA5APCFeStxvouxWKJlLZgoFNxZ9RSzH6Io7BQBVu3We7V/cRjWkiSycTgcmCpX7/d4VPpshtyNi4AAAAAAAAAyAeEK1i0S4Klm7liKLrsCktb9xOPK5lIDSrms57mpxTpP2NpN4IVh6sgJ2MCAAAAAAAAgHxBuIK8deZ0l6Wtt7g15XWlzxquBM4515zBMlqso0N9L72ohSAW6VRX458s7d6i9fKXWmflAAAAAAAAAAAyQ7iCvBQJx9Ta1JPSFrfHFPSPBC6lnhK5HS7LtTanU0WvutTS3vHHB7UQdNQ/oGQyltJms3tUtvz1stlsORsXAAAAAAAAAOQLwhXkbb2VZDK1rT/QIdlHGqvG1FsZrfjKa6QxQUTw4AGFG+o1nwW7jyrYddDSXrL01XK6i3IyJgAAAAAAAADIN4QryEtnTnda2vqL2iettzLEvWSJCnacY2nvuP9ezVfJREwd9fdZ2t3+WgXKz8vJmAAAAAAAAAAgHxGuIC+dqbOGK32FY8OV8WeuGEquvc7S1v30U4q2tmg+6m5+WrFw6tdoKF32WpYDAwAAAAAAAIAsIlxB3olGYmppTK23IkdSwYLOKc9cMfg3b5Fn+YrUxkRC7ffeo/kmFulSd9NjlnZjxoqnYGlOxgQAAAAAAAAA+YpwBXnnbEO3pd5KrKhPyVH1VgxLfBPPXDFme5S9/kZLe9fjf1akuVnzSUfDA0omoiltdodPxbXX5GxMAAAAAAAAAJCvnLkeADAX9VZ6AqlLeTlsDpV5Sya9V+C88+Wqrlb07NmRxnhcbb+5SzXv/6Dmg3DvaQU7D1jajWDF4fTnZEzID0kjpYzHlUwkpERcyXhCyUTcnMFlHA+1mXuzbejcqH0yOXC9cS/jOGn0N46NeyXHtA/0G2kf6jPYbrQZr417D7YNXz987WC72WfkPsZ15msZr80vzjzu8jhlk828LhSKjpzXYP/B49HXDPxv6N6jzg+2DYS7g+cHvpGp1wy3jRyPd83wOMZek/oLNfGv4RT7pj8/9voJ7j3ZvTLqn5xkWNn7Oia9F2bXAl22ss5hjNvYkorHF8jvoYX5rV6A+EbPmQX8/DD+EZfx39EF8/wAMC/UO0f+fXQslsjpWOa9BfrfCGA22D0e9V9wnla85S/4s+osyOtwpb29Xd/97nf1yCOPqKGhQT6fT2vWrNHNN9+s2267TQ6HY1r33b9/v2699dZJ+23dulV33XXXtN4D2a230lHQlPK63Fcqh33yX3+b3a6KW96oxm//W0p7zzNPq+Saa+Vbt165ZPylrOPMQ+MUsd+ZkzFhYslYTMlYVIlIVMloRMmocTywN7eYscUH+sWNvsZmhBgx40/Qg+2D54f7jPTXqP7DfUZdZ4YORkAyGJSYYURKaJIajAAAAAAAci+S6wEAWLDqjx01Py9a9va35XooeSdvw5W6ujq97W1vU0vLyIyFSCSiF154wdx+97vf6Xvf+54CgUDG9963b1+WR4tsiUbjaj6TWm/F7rApGEgNXCp85VO+Z2DX+fKsWq3wyRMp7U0/+ZFWfv7vZXPm7sco2HVQkb56S3vp0utls7HqX6ZBlRl0hENKhsNKGFsopGQkYu4TEeN1WMlwaODc4GYGJJGoEoNBidF/bHgy+rw5OwMAAAAAAACYIx3Pv0C4MgvyMlzp7+/XHXfcYQYrlZWV+sxnPqNLLrlEvb29uvPOO/X973/fDFg++9nP6mtf+9q0w5XzzjvPDGjGM92ZMZi+5jPdShjLBo1SUGFX0p76gXalb+Ji9mNnr1T+xVtU/7//Z0p7pKFe7ffdo/Ibb1YuJJNxdZ75o6XdV7JZnsByLRbGzItEKKhEMKhEf1DxYP/AsdHWb7T3K268NrfBc+b5oZBkJExhpgYAAAAAAADyjX/lylwPIS/lZbjy85//XKdOnZLT6TSDlI0bN5rt5eXl+uQnP6nq6mp94Qtf0P3336/nn3/eDEmmE66cc845KigomJWvAdPTdKbb0uYoTy30bqjMYOaKwb9pswovulg9u59OaW+7+7cq2LZd3lWrNdd6W59XLNw+ptWukpprFm5I0tenuLn1Kt47sCVGv+7rU2L0cX+fGZIAAAAAAAAAGMNuV/H2bVr93nfneiR5yZmPS/v88Ic/NI9vvPHG4WBlNGO5sB//+Mc6efKkfvnLX2YUrsTjcR0+fNg83r59exZHjtkKV0JF3VJiZuGKec1b3qq+l18yZz0Mi8fV+K1/04q/++9yFBZqriTiYXWd/ZOlPVCxSy5v5l/bbDGWwop3dyvW1a14d9fAsbnvUqy7e9TrHnNWCTNH5pjDYc7Mkt0hm8Mum1GHyG6TzZh1Zx98PdhunB/qJ5t9pM/QPcbcyzxnLE3nGNwbBQXNNmNvG7jHYJtxLqV9sG2kfaiPcd/B9uE+Y+45eN5yf6PdKNw2VNjQ7CMVFvrkcNiNevfq6Q0Pn7ON7jfcf+B44NzA9SnnZVw3cjz6vPWaweN01wyN0/xf+mvGFmi01msc0zDp+Yn7m+OY+A0zut9k7z/515Pd9x/+9caiYPxZcabKygrMZ0c8nlB7e19WxoVs4s8TeW8B/xKXlfplN/7sYTw/OvpzPRwY+DsIFojSUv/wnz86eH7kN55LyCaHQxVVJcPPD2RX3oUrBw4cUHNzs3l87bXXpu1jt9t1zTXX6Ac/+IEefvhh8y/ZU/1g5ejRowoN/kv5HTt2ZHHkmCnj1zFduNLhaZZG5SHTDVecxSVa8o7bdfZ730lpj7a26My3/q+WfuwTsrvcmgvdTU8qEUv9w5TN7lZx9RVz9r2O9/Yo1t6uWEeHYh3tiprH7QNtXZ1mcJISRC1WRujgdMnudsnmcsvmGjoeeu2W3TgeanMamzN1cxh7x6hjp2S8HjweaHdY+mtUf/N6MywxrnOkBgiLWOmoD0gTfEAKLArZePIZz23jw1Fj2VHjGACmyu7xmH/2UDwhuzuW6+EAWEAcXu/I88MTz/VwAAD5Gq4M2bp167j9Nm/ebO47OztVX1+v5cuXZ7QkWElJidra2vTVr35VzzzzjNrb21VcXKxdu3bp3e9+d8ZLjWHmujqCCvalLgFWXOpTXXwgbBv9L7DLfGXTeo/Ciy4xZ6/0PLM7pT146KAav/1N1X7wv856gft4tFc9zU9Z2ouqXiWHqyBrS3QZoUm0pdkMj6ItLYq2tg6EJ4NhSjKWH38ZNIMHr9f8i+7A5pUt5dht7u1ej+xuz0Bft8d8bTP2brds7sGAZDA8MYIS+9AxtZcAAAAAAACAvJN34UpDQ4O5N+qtGLVVxlNbWzt8nEm4sn//fnPf19en2267LeVca2urWcfF2D74wQ/q4x//+DS/CkxHw+lOS1tFTUBdkdTZLKXeErns0/utb/xL/yW3v1vhujpFGs+knOt78QU1fP1fVftX/1V2r0+zOWslmUwNNhyuQhUuuSSj+xjhiBGeRM42KtI8KkRpaVGsrXX+hyc2m+w+v+x+nxw+38CxuR84Hm7z+8xfD6PdMfTaOGcGKl7CDwAAAAAAAAAZy7twpaOjw9wHAgE5JvjQtHBUfYyurq4p33/v3r3mPhqNmjNj/vqv/9pcHsxYJunpp5/W1772NTOs+da3vqXS0lJzFgvmxpk04Yq/wi6NqXdeMY0lwUYzPrSv/dBHdfqfvmAWWx+tf99enf7HL6jmg38tz7KpBXaZzlrpbX3O0l5cfaXs9vTLksSDQUWNAKWx0QxSwo1nFDWOW5rNmjHzgc3jlaMwIEeBsRXIEQjIPurYaLePOjba7X7/QN0NAAAAAAAAAJhj8zJc+bd/+zdzua1M3Hrrrfryl7+scHigILHH45mwv9frHT4eumYqYrGYee8LL7zQHKfbPVJj45ZbbtHll1+ut7zlLaqrq9O//uu/6qabblJ5efmsFDKjXsIAu1moWmqoGwjWRiuoTUrHU9uWl1SZhWhnpGyNAv/9czrw918ww4vRjADj9D/+vWrfcItq3nCLnH6/sqXhyCOWWStub6mWrb3ELBofbGhQsH5wa2hQqL5BkfZ25YLD75OruESukmK5iovlKhk8Nvclg20Drx2T/LwCs/38MPYzfi4AWDR4dgCYLp4fAKaL5weA6eL5scjClZmYaLZKNtx5550DxbzjcXPpsbHKysr0N3/zN/rIRz6iYDCoP/zhD3rXu96V9XE4jWLVGBaLxXW2PnX5L6fTrlCBtcB9deGSgSJwM1S8aYO2/H+f0/4v/pPiY2awJGNxNdx5l5ruf0CVV12pqmuvUcHqVTN6v2i4W631T1vaY3s6teebdyjen1rgfjY5i4rkKS+Xu6JcnopyucutewITLCRGWO1wEFgDyAzPDgDTxfMDwHTx/AAwXTw/Fkm48ra3vU3XX399RtcMLfPl8/mmNBslFAqlncUy1d+I6YKVIVdeeaV53pjl8tJLL2m2wgRmrmg4dT3b0K14PJHSXr2sWGf7Tln6LymosPSdroING7T1S1/UwX/8J0VaWy3nYz29arz7D+bmralWYNNGBdavl7eqygwgnIWBgYLqdrsS4YjiwX7F+4NmUBJua1OktU2RtlaFW1oVqmiTbePITClDoiuq0J/rpOx8OcOcRYXyVFWZ4/RULRneeyoq5C4rM4u9TyZb32Ngtp8fxrPUCM0TiWSuhwNggeDZAWC6eH4AmC6eHwCmi+fHiGz8g/t5H64YtUqMbTqKioqGC84bv2HGCyB6enpS3i+bjLDGuGdLS8twDZhs6+iYu1kK850xna3htPX7XL6kQHs6mizt3liB2ttTZ5rMSKBMyz/39zr7w++bRe3HE2o8a26tj/wp8/fwO+S50FrDJb6nc9rBij0QkKemVq7qarmrquWqXCJXZaVcFZVypFnKzKjOYvyu6++LScYG5Mnzw/hXG8YfLrL6XACQ13h2AJgunh8ApovnB4Dp4vkxorJypA573oYrM7Fq1arhgvPNzc2qqqpK2+/MmTPDxzU1NVkfh/H+o2fSYHY1nLIWs6+qLVJLe5ulfaYF7dMxCq3X/tePqOeZ3Wr5xc8U77YuRzYTzp3Fsrnsllkr8UM9k19rLN9VUzuwVdfIXTOwOQsHgkgAAAAAAAAAwCIPVzZs2DB8fODAgXHDlf379w/PdFm2bNmU7v3AAw/oH//xH9Xe3q7vf//7uuiii9L2a2trU2dnZ0rYg9lVfyrNzJXqArWfSW0vdAfkdc5OLRBjllTRRRcrcO5OdT78R3U+8kfF0oQ7GfM55NhaNOGsFWNpMVdVtdzGLJShIMUIUaqqp7SEFwAAAAAAAABgEYcr69ev19KlS9XQ0KCHH35YV111laVPIpHQI488Yh5fdtllU65dUl1draamgWWm/vSnP40brtx9993Dx1dcccU0vxJMVX9fRJ3tqcuk+QNuhV19Sip1HcFKX8Wsj8cIM8pe+zqVXn+DgocOquvJx9W/b++0Z7M4dxRZZq0o4lDp9tfJfV3twJJeFRWyORzZ+QIAAAAAAAAAAIsrXDGCkptvvlnf/OY3ddddd+mtb32rtmzZktLn5z//uU6ePGkev+c975nyvXfs2KHVq1frxIkT+ulPf6o3v/nN5uvRjh07pm984xvm8bZt28YNYJA9TWesocWSmkK1hqyzWSpnYUmw8RhF6v2bt5ibUf8n2tqi0LGjijQ1KdbRrlhHhxKhkJLxuFH9XTa3W3afT3avsXnlLCqSo6xIvcV7lNTAMnNDyta9ToHynXP2tQAAAAAAAAAA8jhcMbzvfe8zgxVjlokRnvzN3/yNrrzySoVCId1555367ne/a/a7/vrrzcBkrE996lN6+eWXzeP77rsv5dxnP/tZfeADHzDv9fa3v12f/OQndckll8jhcJizYb761a+qp6dHfr9fX/rSl+boK17cGuu7LG2VVYVqCTbkNFwZG/q5K5eYWya6m59SsiE1WHG4ClVQav19CwAAAAAAAACYG3kZrgQCAX3rW9/Se9/7XnV0dOjv/u7vLH127dqlr3zlK2mvb2xsNGenpGMs8/XFL35Rf//3f2/WXkl377KyMn3ta1/Tpk2bsvDVYDJnG6zhSkV1QCeDc1PMfrYkE3H1ND9taS+svEg2O0uAAQAAAAAAAECu5GW4YjCWArvnnnv0ve99z6y9cubMGdntdq1du1Y33XST3vGOd8jlck3r3n/xF3+h8847Tz/60Y/01FNP6ezZs3I6nVq+fLmuueYavetd71JpaWnWvyZMPVwxZ64ct4Yrlf6FE670dbyieLQnpc3m8ChQsStnYwIAAAAAAAAA5HG4MjSDxFjiy9gy8ZOf/GTSPmvWrNE//MM/zGB0yIZwKKaOttRi9r4Cl1nQvnUBz1wxarT0ND9laS+sOF92hycnYwIAAAAAAAAADLAP7oEFqa2519JWWV2opJJqDbWntPucPhU4/VoIQj3HFQ21pDbaHOaSYAAAAAAAAACA3CJcwYLWcjZ12ayhJcG6wt2KJWKp7b5ys7D8QtDTstvSVlB2jhyuQE7GAwAAAAAAAAAYQbiCBa21yTpzpaIqoJZgq6XdCFcWgmioTaHuo5b2wsoLczIeAAAAAAAAAEAqwhXk38yV6kK1pKm3slDClZ6WZyxt3sI1cvuW5GQ8AAAAAAAAAIBUhCtYsKKRuKWYvdfnVKDIo5b+hVnMPhELqa/9RUs7s1YAAAAAAAAAYP4gXEFeFbOvqCo066q0ppu54q/QfNfb/oKSiWhKm9NTJm/R+pyNCQAAAAAAAACQinAFC1ZLU7olwQYKvqdbFqzCV6b5LJlMqrflOUt7YeVFZmAEAAAAAAAAAJgfCFeQZ8XsC82QYuzMFZfdpWJ30RyOLnOhnuOKRTpS2mx2jwrKzsnZmAAAAAAAAAAAVoQrWLAS8aSlbUlNofpi/QrFw5ZZK/N99kdv6x5LW0HZDtkd7pyMBwAAAAAAAACQHuEKFqw1G1NrqKzZUKGiEp/agu2WvuXe+b0kWCzSrWDXIUt7oGJXTsYDAAAAAAAAABifc4JzwLy2ekOlbnjjVtUd71BZRYEuvnKNevvCak0Trsz3eit9bS8YVVdS2jwFK+T2LcnZmAAAAAAAAAAA6RGuYMEHLLsuXiWHw654PCH1hdPOXKnwlWu+SiYT6m173tIeqDg/J+MBAAAAAAAAAEyMZcGQd1pD6ZYFK9V8Few6oni0J6XN7vTLX7IpZ2MCAAAAAAAAAIyPcAV5Z6HNXBlYEixVoOxc2exMLAMAAAAAAACA+YhwBYti5krZPJ25YsxYCXYfsbQXVJyXk/EAAAAAAAAAACZHuIK8Ek/E1R7qSGkrdAXkdXo0H/W1v2wtZB9YKZenLGdjAgAAAAAAAABMjHAFeaUz3KVEMpHSVu6bn0FFMplUb9uLlvZA+c6cjAcAAAAAAAAAMDWEK8grbWmWBKuYp+FKpK9OsXBbSpvN7pGvZHPOxgQAAAAAAAAAmBzhCvJKa5pi9uXe+RmupJu1UlC6TXa7KyfjAQAAAAAAAABMDeEK8kpbcGHMXEnEI+rv3GdpLyg/NyfjAQAAAAAAAABMHeEK8kpraGHMXAl2HVIyEU1pc3kr5fbX5mxMAAAAAAAAAICpIVxBXlkoM1f62l+2tBWUnSObzZaT8QAAAAAAAAAApo5wBXldc8Vus6vEU6z5JB7tVajnuKXdX7otJ+MBAAAAAAAAAGSGcAV5IxQLqyfam9JW5imRw+7QfNLfYdRaSaa0eQKr5XQX5WxMAAAAAAAAAICpI1xB3mjpa7O0lc/HJcE6XrG0FZRtz8lYAAAAAAAAAACZI1xB3mhOE67Mt3or0VCrIv1nUtpsNqf8JZtzNiYAAAAAAAAAQGYIV5A3mvtaLW3l3rJ5P2vFV7xRdocnJ+MBAAAAAAAAAGSOcAV5Y77PXEkmk4P1VlKxJBgAAAAAAAAALCyEK8jvmSvzKFyJBs8qFm5PabM7fPIWrc3ZmAAAAAAAAAAAmSNcQV4XtK/wlmu+6O/cb2kzaq3YbI6cjAcAAAAAAAAAMD2EK8gLxpJbY2eueBxuFbj8mj9LgqUJV0q35GQ8AAAAAAAAAIDpI1xBXugO9ygcj6S0VfjKZbPZNG+WBIt0pLTZnX55AqtyNiYAAAAAAAAAwPQQriAvNPVa661UeOdPvZV0hez9xcaSYPwIAgAAAAAAAMBCwye7yAvNaeqtzJdi9saSYH3p6q2wJBgAAAAAAAAALEiEK8gLY+utzKdwJRJsVDzSmWZJsJU5GxMAAAAAAAAAYPoIV5AX5vOyYMF0hexLWBIMAAAAAAAAABYqPt1F3s5cqZgnM1f6uw5Z2vwlLAkGAAAAAAAAAAsV4QryQnOamStl82DmSjTUqlg4tR6M3eFjSTAAAAAAAAAAWMAIV7DgxRJxtQY7UtqK3YVyO1zKtf7Og5Y2X/EGlgQDAAAAAAAAgAWMT3ix4LX1tyuZTM7LYvbBNEuC+Yo35mQsAAAAAAAAAIDsIFzBgtfcl7rslqHcW65ci0d7FOlvSGmz2ZzyFq3N2ZgAAAAAAAAAADNHuII8LWZfqlzr7zpsafMWrZHdnvvlygAAAAAAAAAA00e4gvycueLL/cyVYNp6K5tyMhYAAAAAAAAAQPYQriA/Z654cztzJREPK9R7YkyrTb6i9TkaEQAAAAAAAAAgWwhXsOC1pJm5UpHjmSuh7mNSMpHS5gksl8NVkLMxAQAAAAAAAACyg3AFC17TmJkrDptDxZ4i5VKw+6ilzVe0MSdjAQAAAAAAAABkF+EKFrRgLKTeSF9KW7m3VHZb7n5rJ5PJ9OFKMUuCAQAAAAAAAEA+IFzBgtYWbLe0lfvKlEvRYKMSsd6UNqe7VE5PbpcqAwAAAAAAAABkB+EKFrS20PwLV9LNWvEWrZPNZsvJeAAAAAAAAAAA2UW4ggWtNc3MlQpvjsOVriOWNl/RupyMBQAAAAAAAACQfYQrWNDm28yVeKxfkf6GlDabzSlP4aqcjQkAAAAAAAAAkF2EK1jQ5tvMlVD3MUubEazY7a6cjAcAAAAAAAAAkH2EK8i7gvYVOZy5EuxOtyTY+pyMBQAAAAAAAAAwOwhXsGAlkgnLsmA+p1d+lz8n40kmE2lnrlBvBQAAAAAAAADyC+EKFqzuSI+iidi8WRIsEjyrRDyY0ub0VMjpKc3ZmAAAAAAAAAAA2Ue4ggWrLdhhaSv3lStXQt3HLW2+orU5GQsAAAAAAAAAYPYQrmDBag22WdrKfbmbJRLqsYYr3sLVORkLAAAAAAAAAGD2EK5gwRpbb8VQ4c3NzJVEIqpwX92YVrs8gZU5GQ8AAAAAAAAAYPYQrmDBag1aw5VyX25qroR7T0vJeEqbp2Cp7A5PTsYDAAAAAAAAAJg9hCtYsGJjitkbKnMUrqRfEmxNTsYCAAAAAAAAAJhdhCtYsNaXphaLX1myTJW+ipyMJdRzwtJGuAIAAAAAAAAA+cmZ6wEA03VZ7UUKxUJ6qX2vqgIVeuf2N8oWss35OOLRPkWDZ1PabHa33AW1cz4WAAAAAAAAAMDsI1zBgmWz2XTdyqt0287Xy+GwKx5PqD3UN+fjCPWmm7WySjabY87HAgAAAAAAAACYfSwLBswQS4IBAAAAAAAAwOJCuALMULjnpKXNW7g6J2MBAAAAAAAAAMw+whVgBmKRbsUiHSltdmdATk9FzsYEAAAAAAAAAJhdhCvADIR7T1navIGVZj0YAAAAAAAAAEB+IlwBZiCUJlzxBFbmZCwAAAAAAAAAgLlBuALMwswVAAAAAAAAAED+IlwBpike7VEs3JbSZnf65fRSbwUAAAAAAAAA8hnhCjBNod7TaZcEo94KAAAAAAAAAOQ3whX8/+3dCXTcVb0H8JulTdpSaEspSEGKHqFQLDsoIougVB7IIoK0yiJuWAVFQVBAFBWQp7IIIsoiq8jyWA4KtVZFEPAhgrJr2ZdCl1BK26RZ5p17nxMymUnaydLJzHw+5+Tkn//8//+54ZDbmfn+f/cX6BtLggEAAAAAVCfhCgxguKKZPQAAAABA5ROuQB+0ty4Nrc3zc/bV1o0IwxonlGxMAAAAAACsHsIV6IOWpYX6rbxdvxUAAAAAgCogXIE+aOmhmT0AAAAAAJVPuAJ90LL0xYKVKwAAAAAAVD7hChSpo6M1rFj+Ss6+mpr6MHzEuiUbEwAAAAAAq09VhSuzZ88Om266aTjxxBP7fa1ly5aFCy64IOy7775hyy23DNtss0044IADwsUXXxyam5sHZLwMTSuWvRJCpiNn3/BRE0NNTV3JxgQAAAAAwOpTH6rE888/H0499dQBuVZTU1OYMWNGmDt3bs7+xx57LH39z//8T7j88svDuuuqZKhEK5a+kLevYdQGJRkLAAAAAACrX1VUrjz33HPh8MMPDwsXLuz3tTo6OsLRRx+dgpVRo0aFb33rW+Guu+4Kf/jDH8Lxxx8fGhoawtNPPx2++MUvpmOpPC0Fw5UNSzIWAAAAAABWv4oPV373u9+Fj370o+Hll18ekOvNmjUr/P3vf0/b55xzTpg+fXqqUFl//fXDpz/96XDeeeelx/7xj3+E22+/fUCek6Ejk8kUbGY/XOUKAAAAAEDVqNhwJVaPxAqTWEGyZMmSsOGGG4Y111yz39e97LLL0vftt98+7LLLLnmP77bbbmGnnXZK27/+9a/7/XwMLW0ti0JH27KcffUN40Nd/ciSjQkAAAAAgNWrYsOVuFzXnDlz0va0adPC9ddfH0aPHt2va77++uvh4YcfTtt77LFHj8dlH3vggQfC4sWL+/WcDC2Fqlb0WwEAAAAAqC4VG65EU6ZMCZdcckk499xzw9ixY/t9vSeeeCItC5W9dk8222yz9D32XIkN7qnwZvZr6LcCAAAAAFBN6kOFOv3008OkSZMG9JovvfRS5/YGG/RcrTBx4sTO7RdfzK90oHypXAEAAAAAoGIrVwY6WImampo6t3vr37LGGmt0br/xxhsDPg5Ko6O9ObQ2v5azr7auMfVcAQAAAACgegzJypULL7wwLeVVjAMOOCCceeaZYTC1tLR0bjc2NvZ4XNfHup4zkMaOHRlqamoG5drlpra2pvP7uHGjBu15lix6OW/fqDEbhbXXfitMA8rL6po/gMpi7gD6yvwB9JX5A+gr80eVhStDVV1dXRgq6uuHzliGihg21dUNXuC0fEn+kmBrjNko1NVVbAEYVI3Bnj+AymTuAPrK/AH0lfkD6CvzR5WEK4ceemjYa6+9ijpn9OjRYbCNGDEipyKlvr7wf77m5uZVqnDpj7a2dpUr/xFT1/jfIpPJhI6OzKA9z9LF+c3sR6wxMbS3dwzacwKVMX8AlcXcAfSV+QPoK/MH0Ffmj7cM9E3yQzJcGTt2bPoaarr2WXnzzTfDqFGFy6iWLFnSuT1Yv0dT07JBuW45iuVsMXWNk8OiRUsH7XnefP35vH0tHWsP6nMClTF/AJXF3AH0lfkD6CvzB9BX5o+3rLPOwBZoWM+oCJMmTercfumll3o87uWX3+rN8ba3vW3Qx8Xga2tdEtpb3wrNorrhY0Jd/ciSjQkAAAAAgNIQrhThXe96V+dSXI8//niPxz322GPpezx28uTJq218DJ4VS/Ob2TeMXL8kYwEAAAAAoLSEK0VYY401wrbbbpu258yZ0+Nx2cemTp0axowZs9rGx+BZsSy/Umm4cAUAAAAAoCoJV4q0//77p+933313+OMf/5j3eNz3l7/8JW0fccQRq318DI4Vy/IrV4QrAAAAAADVSbhSwAknnBCmTZuWvro78MADw+abb562jz322HDppZeGefPmpa+4HfdFW265ZcHzKT+ZTKZAuFIjXAEAAAAAqFL1pR7AUPTKK6+EZ555puBjdXV14Sc/+Uk4/PDDwwsvvBDOOuus9NXVxhtvHC666KJQWyu7qgRtK5pCR3tzzr5hjeNDbd3wko0JAAAAAIDSEa70wcSJE8Mtt9wSLr/88nDnnXemkKW9vT1stNFGYa+99gpHHnlkGDVqVKmHyQBZsVS/FQAAAAAA3lKTiWseUXbmz19S6iEMGePGjQp1dbWhvb0jLFq0dMCv3/TinWHJ/Ptz9o3dYO8wep3tBvy5gMqaP4DKZO4A+sr8AfSV+QPoK/PHW9ZZZ3QYSNatgr40sx+lcgUAAAAAoFoJV6AXmUxHWLF8Xu7OmrowvHHdUg0JAAAAAIASE65AL9paFoZMR2vOvuGNE0JNbV3JxgQAAAAAQGkJV6AXK5Z1q1oJIQwbuV5JxgIAAAAAwNAgXIFe5C0JFitXRrytJGMBAAAAAGBoEK5AkZUrw1WuAAAAAABUNeEK9CCTyYTW5a9021sTho3QzB4AAAAAoJoJV6AH7a2LQ0d7c86+YY3jQ23tsJKNCQAAAACA0hOuQDHN7EdYEgwAAAAAoNoJV6AHK/KWBNNvBQAAAAAA4QoU18xe5QoAAAAAQNUTrkAPWpcLVwAAAAAAyCdcgQLaW5eG9tYlOfvqho8JtfUjSjYmAAAAAACGBuEKrGq/FVUrAAAAAAAIV6CIfiua2QMAAAAAIFyBwlqXv5q3T+UKAAAAAACRcAUKWNGcH64MG/m2kowFAAAAAIChRbgC3WQ62kJb88KcfbV1I0Jd/RolGxMAAAAAAEOHcAW6aW2eHyOWnH3DRqwbampqSjYmAAAAAACGDuEKdLOiYL+VdUsyFgAAAAAAhh7hCqxCM/thIyaUZCwAAAAAAAw9whXoZsXy1/L2xWXBAAAAAAAgEq5AF5lMJrQ2d69cqQnDGtcp0YgAAAAAABhqhCvQRUfb0tDRtixnX33DuFBbO6xkYwIAAAAAYGgRrkAXmtkDAAAAALAywhXoQjN7AAAAAABWRrgCXWhmDwAAAADAyghXoIv8ZvYhDG8UrgAAAAAA8BbhCvxHJtMeWpvn5+yrqR0e6oavVbIxAQAAAAAw9AhX4D9amxeGkOnIa2ZfU1NTsjEBAAAAADD0CFeg12b2lgQDAAAAACCXcAX+o/uSYNGwxnVKMhYAAAAAAIYu4Qr8h3AFAAAAAIBVIVyB3sKVERNKMhYAAAAAAIYu4QqEEDo6WkNby6KcfbX1o0Jd/ciSjQkAAAAAgKFJuAIhhLbmBXn7LAkGAAAAAEAhwhXQbwUAAAAAgCIIV6DHfivCFQAAAAAA8glXIIYrywtVrmhmDwAAAABAPuEK9FC5MtyyYAAAAAAAFCBcoep1tK8IbSuacvbV1a8RautHlGxMAAAAAAAMXcIVql5ry4K8ffqtAAAAAADQE+EKVU+/FQAAAAAAiiFcoeq1Nr+Wt2+YfisAAAAAAPRAuELVK9TMXrgCAAAAAEBPhCtUPeEKAAAAAADFEK5Q1TraV4T2FYtz9tUNGx1q6xtLNiYAAAAAAIY24QpVTdUKAAAAAADFEq5Q1YQrAAAAAAAUS7hCVWttfi1v37ARE0oyFgAAAAAAyoNwharWulzlCgAAAAAAxRGuUNUsCwYAAAAAQLGEK1StjvaW0N76Rs6+umFrhdq6hpKNCQAAAACAoU+4QtUq3G9F1QoAAAAAAL0TrlC1WpsX5O2zJBgAAAAAACsjXKFq6bcCAAAAAEBfCFeoWoUrV8aXZCwAAAAAAJQP4QpVq615Yd4+4QoAAAAAACsjXKEqdXS0hrYVTTn76urXCLV1jSUbEwAAAAAA5UG4QlUqVLVSr2oFAAAAAIBVIFyhKrW2WBIMAAAAAIC+Ea5QlVqb5+ftE64AAAAAALAqhCtUpbbmBXn7hjUIVwAAAAAAWDnhClWpVc8VAAAAAAD6SLhC1clkOkJrS27lSk3t8FA3bHTJxgQAAAAAQPkQrlB12la8HkKmPa/fSk1NTcnGBAAAAABA+RCuUHUK9luxJBgAAAAAAKtIuELVaS0QrtRrZg8AAAAAwCoSrlB1CoUrKlcAAAAAAFhVwhWqTvdm9pFwBQAAAACAVSVcoapkMpkCPVdqQ33D2BKNCAAAAACAciNcoap0tC0NHe3NOfvqG8eFmpq6ko0JAAAAAIDyIlyhqhTst6KZPQAAAAAARRCuUFX0WwEAAAAAoL+EK1SVgpUrwhUAAAAAAIogXKGq5DezF64AAAAAAFAc4Qqh2itX6vVcAQAAAACgCMIVqkZH+4rQ3vpGzr66YWuG2rrhJRsTAAAAAADlpz5UkdmzZ4eZM2eGAw44IJx55pl9vs5jjz2WrrEyU6ZMCTfddFOfn4eB1aaZPQAAAAAAA6BqKleef/75cOqppw7ItR599NEBuQ5DYEkw4QoAAAAAAEWqisqV5557LhxxxBFh4cKFAxqubLPNNuEXv/hFj8fV1dUNyPMxeOGKyhUAAAAAAIpV8eHK7373u3DSSSeFJUuWDNg1s+HKlltuGUaNGjVg16UE4Ypm9gAAAAAAFKliw5Wnn346nH322WHOnDnp5w033DAsXrw4vPFGbkPzYrW3t4ennnoqbb/73e8ekLGyerTquQIAAAAAwACo2J4r3/rWtzqDlWnTpoXrr78+jB49ut/X/fe//x2am5vT9tSpU/t9PVaPTKY9tDUvytlXW9cYautVHgEAAAAAUJyKrVyJpkyZEo477riw8847D/iSYGPGjEk9XM4999zw17/+NSxatCistdZaYdttt039XWI/FoaOtpamEEJHXjP7mpqako0JAAAAAIDyVLHhyumnnx4mTZo04Nd97LHH0velS5eGQw45JOexBQsWhDvvvDN9ff7znw9f+cpXBvz56Rv9VgAAAAAAGCgVG64MRrASPfLII+l7a2trqoz5whe+kJYHy2Qy4b777gvnnXdeePHFF8NFF10Uxo4dm6pYGKLhin4rAAAAAABUSrhy4YUXpuW2inHAAQeEM888Mwy2tra20NDQEHbYYYc0zuHDh3c+tt9++4X3v//94eCDDw4vvPBCOOecc8K+++4b1l577QEfx9ixIy1p9R+1tTWd38eNK9xDZckrr+ftG7vOBmGtHo4HqsOqzB8A3Zk7gL4yfwB9Zf4A+sr8UWXhylB2ww03pCqV9vb2UF+f/59v3Lhx4fjjjw/HHHNMWL58ebj99tvDYYcdNuDjqK+vG/BrlrsYNtXVFQ6cWpbNz9s3avS6oa6udjWMDCjn+QOgJ+YOoK/MH0BfmT+AvjJ/VEm4cuihh4a99tqrqHNGjx4dVuf/iIWClaxdd901PR6rXB5++OFBGUNbW7vKlf+IqWv8bxFDr46OTN7jcX/z0tdy9tXU1IW64WNCe3tuk3uguqxs/gAoxNwB9JX5A+gr8wfQV+aPtwz0jfZDMlyJvUriV7lqbGxM458/f35oamoalOdoalo2KNctR7GcLaaucXJYtGhp3uPtrUtCR3tLzr76hrVDU9Py1ThKoBznD4BCzB1AX5k/gL4yfwB9Zf54yzrrDGyBhjWRBklseB+NGDGi1EOpeq3NC/P21TcOfB8cAAAAAACqg3ClCLNmzQq77LJL2GKLLcL999/f43ELFy4Mr7/+/w3UJ02atBpHSCGtLfnhyrAG4QoAAAAAAH0jXCnCeuutF1599dVUlfKnP/2px+Nuu+22zu0YxlBabc0L8vbFZcEAAAAAAKAvhCtFmDp1ath4443T9tVXXx2eeeaZvGPmzp0bfvKTn6TtWOGy4447rvZxsgqVK43jSzIWAAAAAADKn3ClgBNOOCFMmzYtfXX3jW98I9TW1obm5uYwffr0cMMNN4SXXnopzJs3L1x77bVhxowZYcmSJWHkyJHhe9/7XknGT662Aj1Xhum5AgAAAABAH9X39cRK9sorrxSsSsku83X66aeH0047LSxatCh885vfzDtm3Lhx4bzzzguTJ09eDaOlN5mOttC24v/732TV1o8KtXWNJRsTAAAAAADlTbjSBwcddFDYZpttwi9/+ctw7733pqqV+vr6sOGGG4YPfOAD4bDDDgtjx44t9TBJS4ItihFLzj5LggEAAAAA0B9VFa7MmTNnlY678sorV3rMO97xjvDtb397AEbFYGor1G9FM3sAAAAAAPpBzxUqWmvzgrx99fqtAAAAAADQD8IVKprKFQAAAAAABppwhSqsXNFzBQAAAACAvhOuULEymUxo7V65UlMX6oePKdWQAAAAAACoAMIVKlZH29KQaW/J2TesYVyoqfG/PQAAAAAAfedTZipWXtVKXBJMvxUAAAAAAPpJuELFaivQb2VYo3AFAAAAAID+Ea5QsVqbC1WuaGYPAAAAAED/CFeoqmXBVK4AAAAAANBfwhUqVluhcEXPFQAAAAAA+km4QkXKdLSFtpamnH219aNCbf2Iko0JAAAAAIDKIFyhIv1/sJLJ2adqBQAAAACAgSBcoWr6rdTrtwIAAAAAwAAQrlCRWpsX5O0b1jC+JGMBAAAAAKCyCFeonmb2KlcAAAAAABgAwhWqpnKlXs8VAAAAAAAGgHCFipPJZPIrV2pqQ33D2FINCQAAAACACiJcoeJ0tC0LHe3NOfvqG8aFmhr/uwMAAAAA0H8+babitLYUamZvSTAAAAAAAAaGcIWK09ZcoJm9cAUAAAAAgAEiXKHitHbvtxKXBWscX5KxAAAAAABQeYQrVJzW5gLLgjWqXAEAAAAAYGAIV6g4bYUqVxpUrgAAAAAAMDCEK1SUTEd7aGtpytlXWz8y1NWPKNmYAAAAAACoLMIVKkrbihisZHL2aWYPAAAAAMBAEq5Q8f1WNLMHAAAAAGAgCVeo+H4rKlcAAAAAABhIwhUqSmtzgWb2jcIVAAAAAAAGjnCFitLakr8smMoVAAAAAAAGknCFitKWV7lSG+obxpZoNAAAAAAAVCLhChWjbcXS0NG+PGdfDFZqaupKNiYAAAAAACqPcIWK0bxsft6+YfqtAAAAAAAwwIQrVIyWAuFKfcP4kowFAAAAAIDKJVyhYrQsVbkCAAAAAMDgE65Q2cuCNQhXAAAAAAAYWMIVKntZsEbLggEAAAAAMLCEK1SETEd7aFm+MGdfbd2IUFc/smRjAgAAAACgMglXqAgpWMl05Oyr128FAAAAAIBBIFyhIjQXambfYEkwAAAAAAAGnnCFyg1XVK4AAAAAADAIhCtUhOZCzexVrgAAAAAAMAiEK1SE5qWv5e1TuQIAAAAAwGAQrlARWvKWBasJ9cPHlmg0AAAAAABUMuEKZa+tdVloa12as6++YWyoqa0r2ZgAAAAAAKhcwhXKXkuBfivD9FsBAAAAAGCQCFeoyH4r9fqtAAAAAAAwSIQrlL2WZQvy9g1rEK4AAAAAADA4hCtU5LJgKlcAAAAAABgswhXKXvNSPVcAAAAAAFh9hCuUtUymI6xYvjBnX21dY6itH1myMQEAAAAAUNmEK5S1tpamkMm05+yrb1g71NTUlGxMAAAAAABUNuEKZa2tJbdqJRrWaEkwAAAAAAAGj3CFstbanB+uxMoVAAAAAAAYLMIVylpry4K8fSpXAAAAAAAYTMIVylpbgcqVYSpXAAAAAAAYRMIVylprXs+VmlDfMLZEowEAAAAAoBoIVyhbHW3LQ0fb0px9MVipqa0v2ZgAAAAAAKh8whUqqGpFM3sAAAAAAAafcIWy1arfCgAAAAAAJSBcoWy1tSzI2zescXxJxgIAAAAAQPUQrlC22lqa8vbVN6pcAQAAAABgcAlXKFu1dY05P8dG9sMbJ5RsPAAAAAAAVAfhCmVr9IT3hJra4Z0/T3j7LqG2fkRJxwQAAAAAQOWrL/UAoK9if5X1pxwT6tpfCCPWGB9GjH57WLRoaamHBQAAAABAhROuUNbq6keGcRO2CXV1taG9vaPUwwEAAAAAoApYFgwAAAAAAKAIwhUAAAAAAIAiCFcAAAAAAACKIFwBAAAAAAAognAFAAAAAACgCMIVAAAAAACAIghXAAAAAAAAiiBcAQAAAAAAKIJwBQAAAAAAoAjCFQAAAAAAgCIIVwAAAAAAAIogXAEAAAAAACiCcAUAAAAAAKAIwhUAAAAAAIAiCFcAAAAAAACKIFwBAAAAAAAognAFAAAAAACgCMIVAAAAAACAIghXAAAAAAAAiiBcAQAAAAAAKIJwBQAAAAAAoAg1mUwmU8wJAAAAAAAA1UzlCgAAAAAAQBGEKwAAAAAAAEUQrgAAAAAAABRBuAIAAAAAAFAE4QoAAAAAAEARhCsAAAAAAABFEK4AAAAAAAAUQbgCAAAAAABQBOEKAAAAAABAEYQrAAAAAAAARRCuAAAAAAAAFEG4AgAAAAAAUAThCgAAAAAAQBGEKwAAAAAAAEUQrgAAAAAAABRBuAIAAAAAAFAE4QoAAAAAAEARhCsAAAAAAABFEK4AAAAAAAAUob6Yg2GoePLJJ8MvfvGLcP/994dFixaFMWPGhC222CJMnz497LLLLqUeHjDI/vSnP4Ubb7wxPPTQQ2kOGD58eNhoo43CrrvuGg477LAwbty4gue1traGa6+9Ntx6661h7ty5IZPJhIkTJ4Y999wzHHnkkWku6Y25ByrLsmXLwgEHHBCeffbZ8MUvfjF86UtfKnicuQN48803wxVXXBFmz54dnn/++dDS0hLWX3/99NrjqKOOCuuuu26vc81ll10W7rjjjnRuXV1det3y4Q9/OL1uaWxs7PW5H3jggXD55ZeHBx98MLzxxhvpdc62226bzt16660H4bcFBtK9994brrrqqvDwww+H119/PYwaNSpMnjw5vQb5yEc+EmprC9/37PUHVJ/vfve74corrwxnnHFGOPDAA3s9tpRzRH+fu5LUZOJvD2Xk97//fTj22GPTH3Ihn/zkJ8PJJ5+82scFDL62trZw4oknhttuu63HY9Zee+1wwQUX5H3YED8E+fSnPx3++te/FjxvwoQJ4ZJLLgmbbLJJwcfNPVB5Tj311HDdddel7Z7CFXMH8MQTT4TPfOYz4bXXXiv4ePwA4ec//3mYOnVq3mNNTU1hxowZ6YOHQt7xjnek4KSncObqq68Op59+evrQorv4gezXvva1FO4AQ9NZZ50VLr300h4f33nnndN7l+4hq9cfUH3iDRzx/UhHR8dKw5VSzhH9fe5KY1kwyspjjz0WjjvuuPTH/+53vzuluffdd1+44YYbUjoaxX3xTQhQeX74wx92Bit77LFHulMizgFxX/xwYeTIkWHhwoXh85//fHj11Vdzzj3ppJPSP/7Dhg0LX/nKV9KLiT//+c/pzpC11lorfWASz4t3l3Zn7oHK88c//rEzWOmNuQOq2/z588Phhx+e/tZHjx6dQtk5c+aEWbNmpflhxIgR6U70mTNnpuqWruKHI0cffXQKVuKd6t/61rfCXXfdFf7whz+E448/PjQ0NISnn346hbvx2EKVunGuicHK+9///nD99denOSTOGdttt1065+yzz07XA4ae+DebDVa22mqrFKTec889qQJ/n332Sfvvvvvu8J3vfCfvXK8/oLrE1xZf/vKXC74eKKSUc0R/nrsixcoVKBef/exnM5tssknmgx/8YObNN9/MeayjoyNzzDHHpMd32GGHzJIlS0o2TmDgzZs3L7P55punv/GvfvWrBY/5xz/+0XnMt7/97Zz9cV/8uuaaa/LOe/TRRzNTpkxJj//0pz/Ne9zcA5Vl4cKFmZ122qlzXohf5513Xt5x5g7guOOOS3+nW221VZoTuvvDH/7QOU9cddVVOY/99re/7XzsT3/6U6/n3nrrrXlzxD777JMe+/jHP55pbW3NebylpSVzyCGHpMf32muvTHt7+4D9zsDA2HPPPdPfaPxbbm5u7nF+2XTTTdN7nSyvP6B6xH+/zz333MzkyZNz3pvceOONPZ5Tyjmiv89diVSuUDbiHV/xLtPoc5/7XLr7q6uampq0XFAsj493j/3ud78r0UiBwSqRjcuCRfHuiELiXRfZOy2y80UU1zmPNthgg3DwwQfnnbf55puH/fffv/MOs67MPVB5Yon7ggULVrqOsbkDqlucJ37729+m7ViBEl9ndLfbbruFSZMmpbs3H3300YJzyPbbb19w7fJ47k477ZS2f/3rX+c8Fu9mf+qpp9J2XLajvj63XWrsNxerX6Jnnnkm9WUBho74b3vssRTFviqxUq27Qw89NH2P1Wn/+Mc/Ovd7/QHVIVZ77LfffmlpwFixMmXKlFU6r5RzRH+eu1IJVyirSSf7h7777rsXPOZtb3tb2GyzzTo/iAUqRywtjWsRjx8/PjVK60lsEJs9PvtmJTt/xLkjNpEtJC4zFr344otpbfUscw9UlvgiP5aux3nkm9/8Zo/HmTuAO++8M7S3t6elvz7xiU/0eFxs5vrII4+E73//+5374gcSsXl113mikOxjMRxZvHhxzpJg0ZprrpnCmUK22WabMHbs2LRtDoGhpWuT+uwNYt3FULb78V5/QPWIfUvijRRxLoi9Vs4555yVnlPKOaK/z12phCuUjccffzx9X3/99cO4ceN6PC6mpFH3O8eA8harVeKHFPGDjt4899xz6Xtc6zP7D/obb7yRtnu7EyQ7d0TxA5Iscw9UjngHafzwM76ZiE0i11hjjR6PNXcA2TvJY8VK7OvWVdcGsIXuSI8fJmSb0Pc2h2Q/vIh3rMY10LueH02ePLnHDy/iXJY93xwCQ0sMRmNVW3T77beHFStW5B0Te69E8YPVbGWc1x9QPeK/4x/60IfCLbfckvqvdQ1le1LKOaK/z12phCuUjZdeeqmz9Kw3cYKI5s2b1+MdIkD56u3D0NjEPtvUddttt82ZO1Y2f6yzzjqdd4/FFw1Z5h6oDPHu8xNOOCE1VjzssMPCjjvu2Ovx5g7gX//6V/qe/YA0Vr0deeSRYeuttw5bbLFF2HnnncNpp52WXn/0dQ7pWo3bnzmk67nA0PDVr341fVga55I4d8SG0QsXLkzh6SmnnBKuu+66zmUHJ0yYkLa9/oDqEZcePf/888M73/nOVT6nlHNEf5+7UglXKBtNTU05d6P3ZPTo0el7vFMsm6gClS/+zZ966qmhpaUl/Tx9+vScuSN7B1lP4huf7HqjXecOcw9Uhp/97Gfh73//e3rzEj/sWBlzB5BdYjT+HcfXGF/4whfCX/7ylxTSRvPnzw/XXntt6qcQ55e+zCFdbxrpzxxi/oChJ96R/pOf/CQFtHHpv8MPPzz1WYo9FmKfpbj0zllnnRVmzpzZeY7XH1A9Nt5446LPKeUc0d/nrlTCFcpG9gPTQmX3XcWeDFmFSm+ByhSX+Mk2Zttnn33Ce97znpy5o/v8UEh2ful6jrkHyl8sR7/wwgtTQ+gf/OAHK/17jswdwNKlS9P3m2++Od1hvt1224Wrr746LRd27733psAlLhcW+6vE4CUbxhQzh3R9rC9zSKH5Bxg63nzzzbxlBbNiFcuDDz4YFi1a1LnP6w+gN6WcI/r73JVKuELZ6GmtYaC6xTspYrDyy1/+Mv28ySabhO985zsDNneYe6C8NTc3h+OPPz71R4jLbsSlfFaFuQOI80e2QiUuJXj55ZengCV+YBDXKZ8xY0a4+OKL0x2a8cPRuJ1lDgG++93vpiVJYz+lQw89NPzmN78J//znP8Ndd90VTj755DB8+PAU3H7iE58ICxYsSOeYO4DelHKOML8UJlyhbIwYMWKV7qrIvgmKVuXOVKB8xfkgvmGJH3ZEcbmfSy+9tLMEtevcsSp3TWQf73oXhrkHylusVHn66adTo9jPf/7zq3yeuQPo+jd94okndq4f3tX2228fdt1117Q9a9asoueQrnNAX+aQVb0DFVi94hKCV155ZdqOy5HG/kzxvUoMVNZdd93wyU9+MlXCxaqWuXPnhh/96EfpWK8/gN6Uco7o73NXKuEKZSO73t+SJUt6PS67nl9MVFe2hiBQvuISHJ/61KfCrbfemn6eMmVKuOqqq1LztK66rgXa2/zR0dHRufzH2LFjO/ebe6B8/fnPf04fXMQ3BHFN87gs2KoydwDZmzXi3/Pmm2/e43E77LBD+h4b28clgLrPIdl9hXSdI/ozh3Q9Fyi92FMlin1VjjrqqILHTJ48OXz84x9P27fccktYvny51x9Ar0o5R/T3uSuVcIWya/T08ssv93rcK6+8kr7Hu0FiiT5QeZ5//vlwyCGHhP/93/9NP7///e9Pd4bFJTq6iw0ks3qbP+KSH3HZoOyboCxzD5Sv22+/vfPOqb333jtsuummeV9ZseFsdt+LL75o7gDCBhtssEp3dXdtSp+907PrHPLSSy/1eG7XOaI/c8j666/f63HA6vXss8+m71tuuWWvS+lkw9m2trb0HsfrD6A3pZwj+vvclcoMStmIfRSiF154ode7v+J6ptFmm2222sYGrD7/+te/UrCSfcNy8MEHh4suuihnKbCuJkyYEMaMGZMzPxTy6KOPdm53vTvV3APVydwBZP8uYz+V3v6Os70S4rJh2Rs93vWud4Wampq0/fjjj690DojHxrvYu88hTzzxROovV0jcn722OQSGluwHi8U0i4/Hev0B9KaUc0R/n7tSCVcoG9m1jNvb28Mf//jHHpPV7BuMeCc7UFniC4AjjzwyfcgRHXvsseH0009f6VI/2fkjzh09fUAxZ86c9D0uK9b1ww1zD5Sv73znO+HBBx/s9Svrc5/7XOe+iRMnpn3mDqhuu+22W+fyFrNnz+7xuHvuuSd9nzp1aufdnbGaZdttt82ZJwrJPhbPzX5gEe2yyy7p+8KFC8NDDz1U8Nw4XzU1NaVtcwgMLdm7w+PfaW8BywMPPJC+x/czG220Udr2+gPoTSnniP48d6USrlA2Ntxww843KOeff37e+n7xj/rMM89Mb37imn777bdfiUYKDNbdX1/+8pdTiWl00kknhS984QurdO4BBxyQvsem1tdcc03e4/Gui5tvvjltH3744Z13mkbmHihfsWlsrGrr7Ssr3nGe3ZedA8wdUN3e9773dYatP/7xjzsrVLq64447Oj8czc4ZWfvvv3/6fvfddxf8ACPui02voyOOOCLnsR133LHzuX/wgx/kfTgbf/7v//7vzioZH5DC0BKXI832iYzzRyH//ve/O19fxEA128/A6w+gN6WcI/rz3JVKuEJZiR+mxrvB4nJA06dPT29U4h3sseTsS1/6UnpzE8XtkSNHlnq4wAC67rrrwiOPPJK2P/zhD4ePfexjqUlab19Z733ve8MHPvCBtP29730vvcGJVTAxqLnhhhtSNUwMb+La6oceemjec5t7oDqZO6C6xTvJYwVc/DueN29eWoo0Np2OjetjH5W4LOnXvva1dOxWW20VDjzwwJzz48/Z5TBite2ll16arhO/4nbcl+3JMG3atJxz43PGOSR75/unPvWp8Le//S1VqsTv8ee4P35ocdxxx1XFhxdQTuL7lfe85z1pO/69x3/rY7/I+Dog9naL/SLja4Nly5alBtMnnHBC57lefwC9KeUc0d/nrkQ1mZ5qeGCIuummm8Ipp5ySGr4VEv+QTzzxxNU+LmBwffCDH0xNHovx5JNPdm4vXrw4HHXUUeGf//xnwWPHjx+f7rzIluN3Z+6BypRtav/FL34xvYHoztwB3H777eEb3/hGZ7P67qZMmRIuvPDCsN566+U9FkOYeOdm/OChp6WD4hyS7dXS3QUXXBDOO++8go/FQCWO67DDDivq9wFWjzfeeCOFqNkKtZ5eR8S/8eyd5Flef0D1icHrHnvskbbPOOOMvJs2hsoc0d/nrjTCFcpS/MD0kksuCffff39ahzgmqVtssUVKXPfcc89SDw8YYPEuiniHRLG6hitRvIPi2muvDbfddluYO3duWlIjLrmx++67h8985jNh7bXXXun1zD1QXeFKZO4AXn755XDZZZeFu+66K1WeNDQ0pGDkIx/5SPjoRz8aGhsbezw3VtNefvnl4c4770whS1znPH7gsNdee6UPL7ouUVhIXHbsiiuuSBUrcYmhuHTQ1ltvnZYS22GHHQbhtwUGSlxaZ9asWWmZnFiFH/+G43wxadKkdPf3jBkzwlprrVXwXK8/oLoUE66Ueo7o73NXEuEKAAAAAABAEfRcAQAAAAAAKIJwBQAAAAAAoAjCFQAAAAAAgCIIVwAAAAAAAIogXAEAAAAAACiCcAUAAAAAAKAIwhUAAAAAAIAiCFcAAAAAAACKIFwBAAAAAAAognAFAAAAAACgCMIVAAAAAACAIghXAAAAAAAAiiBcAQAAAAAAKIJwBQAAAAAAoAjCFQAAAAAAgCIIVwAAAAAAAIogXAEAAAgh3HHHHeGJJ54o9TAAAIAyIFwBAACq2oIFC8LMmTPDscceGxYvXlzq4QAAAGVAuAIAAFS1u+66K8yePbvUwwAAAMqIcAUAAAAAAKAIwhUAAAAAAIAiCFcAAAAAAACKUJPJZDLFnAAAADBUzZs3L1x11VXh7rvvDs8991xoa2sL48aNC5tvvnn40Ic+FD7ykY+Eurq6dOxNN90UTjrppB6v9eSTT+bte/XVV9P1Y5+WF198MV1/woQJYccddwwzZswIm222WcFrdX2uWbNmhfHjx4eLL7443HHHHeGVV14JDQ0NYcqUKeHggw8Oe++9d6+/41/+8pdwww03hAcffDAsWLAgnZsdw0EHHRS22GKLIv+rAQAAxRKuAAAAFSGGDjNnzgzLli3r8ZhNN900XHbZZWHttdcuOly5+eabw7e//e0er19bWxs++9nPhi9/+cuhpqYm57Guz/WrX/0qnHLKKeFf//pXwevstdde4Yc//GEYNmxYzv741u20005L5/ckPu9RRx0Vjj/++B6PAQAA+k+4AgAAlL1FixaFadOmhcWLF4fhw4eHj370o2HLLbdMVR2xwuT6668Pzz//fDp21113TVUjL7/8cnjsscfCfffdF6688sr02LHHHhs22WSTtL3nnnt2Xv+WW24JX//611PAEUOPfffdN2y//fbpuZ566qlUSbJw4cJ07Gc+85nwta99rcdwZeONNw7PPPNMqjaZPn16ePvb3x7mzp0brrnmmtDU1JSO2WeffVLA0lX8HU4++eS0vdFGG4UDDzwwndvc3Bz++c9/hhtvvDG0tLSkx88555zw4Q9/eND+ewMAQLUTrgAAAGXv8ssvD2eccUba/vGPf5y3tFYMIGKQ8eijj6afZ8+eHTbccMO84OOKK65Iy2t1XwosBjexYiVWvFx66aVh8uTJOcfEUCdWrTz00EOpeiRWl2y11Vadj3evkolLgMXrjBkzJud5DjvssPDss8+mn+PyYzHAydpvv/3CE088EdZdd91w66235pwb/e1vf0vnx6XK4nnxfAAAYHBoaA8AAJS9WAmSFStTumtsbEwVJbHiY+edd+6sEFkVV199dedSYN/97nfzgpVorbXWCmeddVaqaon3r11yySU9Xm/EiBHh/PPPzwtHYmhy9tlnd/4cw5dCv2MMbbqfG2277bZhjz32SP1l1ltvvVX+/QAAgOLV9+EcAACAIaVr2BCDjS996Ut5fU/iMll9WSorNp2PYtXK7rvv3uNxkyZNSgFHXGbs7rvvThUk9fX5b7niGCZOnFjwGlOnTk3hSayAiddZsWJFWnos+zvG6pZ77rknLWcWQ5TuzjvvvKJ/PwAAoHjCFQAAoOzFZbt+9rOfpaqRCy64IPzmN78JH/rQh8Iuu+ySwopCIceqiBUuzz33XNpeY401wu9///tej48VMlGsdHn66ac7+7d0tdNOO/V6jW222SaFK/EaTz75ZHj3u9/d+Tv+8pe/DG+++WY46KCD0nVi2BN/x+wSZwAAwOohXAEAAMreZpttlprRx0bu2SW0YtgSv0aPHh3e9773pbAlLpuVDUBWxWuvvda5HUOWmTNnrvK52Qb3hSpcerP++usXvMYxxxwTHnjggdQ3pr29Pfz5z39OX9lrfuADH0hVMbH6BQAAGFx6rgAAABXh6KOPTo3tY0+Vurq6zv1LlixJS3sdd9xxYbfddgu33377Kl8zVon01dKlSwvuHzVqVK/ndQ1/uj5/rJz51a9+Fb761a+Gt7/97TnnPPvss6lHy8c+9rEwY8aM8MILL/R53AAAwMqpXAEAACrGe9/73vS1aNGicNddd6X+JPfee2+YP39+5zJfMZyIQUWhxveFms9n7b333uHHP/5xv8cY+6j0Ji4HljV27Nicx2L/lc9+9rPp64knnuj8HR988MHO68bqliOPPDLcdtttOeMHAAAGjsoVAACg4owbNy7sv//+4eyzz05LZ8WKj9ibJIp9WX7605+u0nViE/usbEDTX7EpfW9efPHFzu0JEyb0eNzkyZNTyBL7sNx3333hrLPOCuuss056LFauxHAFAAAYHCpXAACAshbDkrjs19y5c1NFyhFHHJHzeE1NTdh6663DhRdemPqSxD4qsVH8qlh33XVTwBHPeeSRR1JVyciRI3s8Pla2LFiwIGywwQZh+vTpYa211so7JlaZ9FY187e//a0z2HnnO9+ZtufNm5eqVJ5++unUV2XLLbfMW2oshkmx0iUGLtGq/o4AAEDxVK4AAABlLYYnP/zhD8P555+fApSelt0aNmxYZ7+Trn1PamvfelvU0dGRd94ee+yRvi9fvjxcc801PY4j9j35+c9/Hm644YZUTdJTb5Wbb745XauQbMP6aPfdd+8cW6xmOeWUU8Jll10Wbrnllh7H0DXM6S0EAgAA+ke4AgAAlL1p06al74sXLw7f//73UzVLd7Nnzw7PPPNM2t5uu+0KNpB/44038s47/PDDUzATnXvuuWHOnDl5x8TzjjnmmNDe3p5+/uQnPxnq6wsvFBCrUE4++eTQ1taWs/+ll14KX//619N2fL5Pf/rTnY9ttdVWqYom+vWvf51CmO7i73zJJZd0/tz1dwQAAAZWTabQuw4AAIAyEhvYx+WyXn/99fTz5ptvnn6eOHFiClziUlu/+c1vUmVKQ0NDCihiz5LooYceCoccckjafte73hU+97nPpZBkn3326QxIrrjiivC9730vp5plt912Sw3j//3vf6frxTFE8brx5/g8WTfddFM46aSTOitt4tuwTTfdNBx00EFh/Pjx4fHHHw/XXnttWLJkSTomBjUzZ87M+R1vvPHG8I1vfCNt19XVhf/6r/9KoUusVnnllVfCrbfeGp566qn0+DbbbJOuBwAADA7hCgAAUBH+/ve/h6OPPjo0NTX1eMyaa66ZGr/H3itZra2tKah47rnnco6NYUy250l01VVXpXN7WnYsimFHXJos9kvpqmu4EnuixKXBYh+X7mLwcuyxx6bfo5Af/ehH4eKLLy5YmdN1DD/96U/DuHHjejwGAADoH+EKAABQMWL1yK9+9avU/D0uAfbmm2+mJvexwXzsYfLxj388VYp0F5fkisHJX//611Q9EqtBYh+X9773vTnHvfzyy+Hqq68O99xzT+qDEnunjBkzJlXK7LvvvimkiVUl3XUNV84444wU7lx00UVh1qxZKWSJ19hxxx3TEmRTp07t9Xd8+OGHw3XXXRcefPDB8Oqrr6ZwKAYpcQx77713qrjp2kcGAAAYeMIVAACAQdY9XDnwwANLPSQAAKAf3M4EAAAAAABQBOEKAAAAAABAEYQrAAAAAAAARRCuAAAAAAAAFEG4AgAAAAAAUISaTCaTKeYEAAAAAACAaqZyBQAAAAAAoAjCFQAAAAAAgCIIVwAAAAAAAIogXAEAAAAAACiCcAUAAAAAAKAIwhUAAAAAAIAiCFcAAAAAAACKIFwBAAAAAAAognAFAAAAAACgCMIVAAAAAACAIghXAAAAAAAAiiBcAQAAAAAAKIJwBQAAAAAAoAjCFQAAAAAAgCIIVwAAAAAAAIogXAEAAAAAACiCcAUAAAAAAKAIwhUAAAAAAIAiCFcAAAAAAADCqvs/aiDKe7ZqLaYAAAAASUVORK5CYII=",
"text/plain": [
""
]
},
"metadata": {
"image/png": {
"height": 1011,
"width": 811
}
},
"output_type": "display_data"
}
],
"source": [
"fig, ax = plt.subplots(\n",
" nrows=3,\n",
" ncols=1,\n",
" figsize=(8, 10),\n",
" sharex=True,\n",
" layout=\"constrained\",\n",
")\n",
"for axis, data, name in zip(\n",
" fig.axes,\n",
" histories,\n",
" [\"cross-entropy\", \"alpha\", \"beta\"],\n",
"):\n",
" axis.plot(data)\n",
" axis.set(title=name)\n",
"\n",
"axis.set(xlabel=\"steps\")\n",
"\n",
"fig.suptitle(\"Training\", fontsize=18, fontweight=\"bold\");"
]
},
{
"cell_type": "markdown",
"id": "af29f666",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"`make_classification` doesn't return true parameters to check against, so we'll just look at the confusion matrix. Seems like we learned something. It's a toy problem anyway!"
]
},
{
"cell_type": "code",
"execution_count": 54,
"id": "cacdee5b",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"data": {
"text/plain": [
"array([[36, 14],\n",
" [11, 39]])"
]
},
"execution_count": 54,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"from sklearn.metrics import confusion_matrix\n",
"\n",
"\n",
"confusion_matrix(y, predict_fn(X, alpha, beta, 0.5)[1])"
]
},
{
"cell_type": "markdown",
"id": "7fbb667d",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Taking a step back\n",
"\n"
]
},
{
"cell_type": "markdown",
"id": "f1338584",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"### How does it compare with alternative frameworks\n",
"\n",
"* Graph is built explicitly with placeholder inputs (common source of confusion for users)\n",
"* It is focused on array (tensor) operations (dense and sparse). Tries to look almost like numpy / scipy, (until the abstraction breaks).\n",
" * There is narrow / hidden support for other types like scalars, lists, slices, random Generators, strings, None (although easy to extend)\n",
"* Functional design (there is no variable mutation when defining graphs)\n",
"* Strong focus on hackability / graph manipulation\n",
"* Evolved from:\n",
" 1. Theano which strongly inspired Tensorflow 1.x and JAX. Many concepts stood the test of time. Others have aged and provide some drag.\n",
" 2. Aesara, which cleaned up the codebase, added alternative backends (Numba and JAX) and proved there's some interest out there in a library like this."
]
},
{
"cell_type": "markdown",
"id": "12420067",
"metadata": {},
"source": [
"We hope you enjoyed this introduction to PyTensor. This is just the beginning of what you can do with it. Please explore the documentation and the gallery for more examples and applications."
]
},
{
"cell_type": "markdown",
"id": "556202cf",
"metadata": {},
"source": [
"## Authors\n",
"\n",
"- Jesse Grabowski and Ricardo Vieira in August 2025"
]
},
{
"cell_type": "markdown",
"id": "f06cf7a2",
"metadata": {},
"source": [
"## References\n",
"\n",
":::{bibliography} :filter: docname in docnames"
]
},
{
"cell_type": "markdown",
"id": "4b3d194f",
"metadata": {},
"source": [
"## Watermark "
]
},
{
"cell_type": "code",
"execution_count": 55,
"id": "8277fb12",
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Last updated: Sun Aug 17 2025\n",
"\n",
"Python implementation: CPython\n",
"Python version : 3.12.11\n",
"IPython version : 9.4.0\n",
"\n",
"pytensor: 2.31.7\n",
"\n",
"pymc : 5.25.1\n",
"scipy : 1.16.1\n",
"pytensor : 2.31.7\n",
"IPython : 9.4.0\n",
"sklearn : 1.7.1\n",
"matplotlib: 3.10.5\n",
"graphviz : 0.21\n",
"numpy : 2.2.6\n",
"\n",
"Watermark: 2.5.0\n",
"\n"
]
}
],
"source": [
"%load_ext watermark\n",
"%watermark -n -u -v -iv -w -p pytensor"
]
}
],
"metadata": {
"celltoolbar": "Slideshow",
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.12.11"
}
},
"nbformat": 4,
"nbformat_minor": 5
}